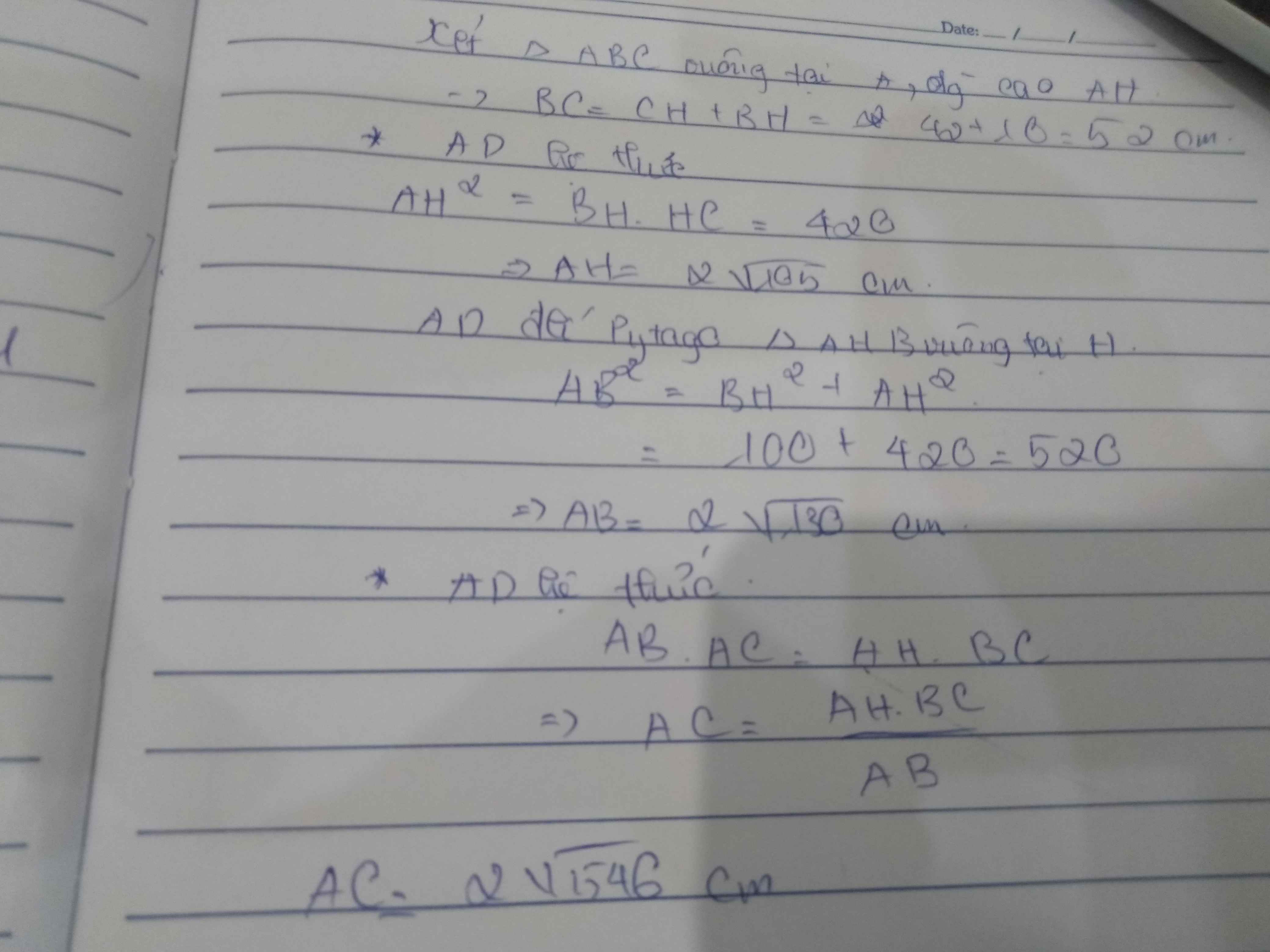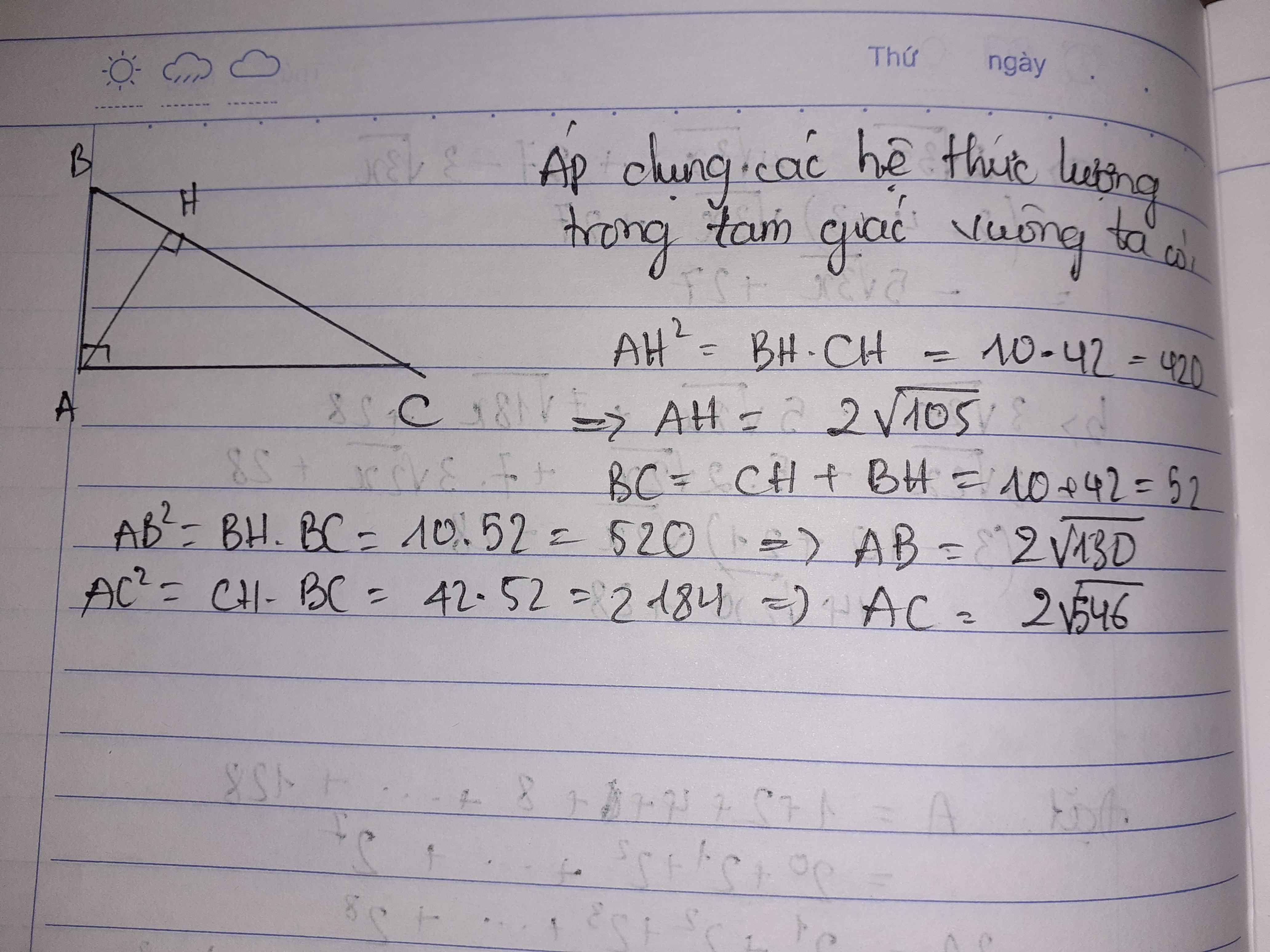Cho tam giác ABC vuông tại A đường cao AH, biết BH=10cm, CH=42cm. Tính cạnh BC, AH, AB và AC

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường cao AH, biết BH=10cm, CH=42cm. Tính cạnh BC, AH, AB và AC ( vẽ hình giúp )
* Cho tam giác ABC vuông tại A có đường cao AH. Biết BH=10cm, CH =42cm. Tính BC, AH, AB và AC
Cho tam giác ABC vuông tại A , đường cao AH . Biết BH = 10cm , CH = 42cm . Tính BC , AH , AB , AC.
\(BC=BH+CH=52\left(cm\right)\)
\(AH=\sqrt{BH.CH}=2\sqrt{105}\) (cm)
\(AB^2=BH.BC\Rightarrow AB=\sqrt{BH.BC}=2\sqrt{130}\left(cm\right)\)
\(AC^2=CH.BC\Rightarrow AC=\sqrt{CH.BC}=2\sqrt{546}\left(cm\right)\)
Đúng 5
Bình luận (0)
Ta có: BC=BH+CH(H nằm giữa B và C)
nên BC=10+42=52(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow AH^2=10\cdot42=420\)
hay \(AH=2\sqrt{105}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow AB^2=\left(2\sqrt{105}\right)^2+10^2=420+100=520\)
hay \(AB=2\sqrt{130}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=52^2-520=2184\)
hay \(AC=2\sqrt{546}\left(cm\right)\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
* Cho tam giác ABC vuông tại A có đường cao AH. Biết BH=10cm, CH=42cm. Tính BC, AH, AB và AC
* Hình thang cân ABCD có AB=30 cm, đáy nhỏ CD=10cm và góc A là \(60^0\).
a. Tính cạnh BC
b. Gọi M,N lần lượt là trung điểm AB và CD.Tính MN
Cho D ABC vuông tại A có AB = 6cm, AC = 8cm, BC = 10cm, đường cao AH a) Viết các hệ thức giữa cạnh và đường cao AH trong tam giác ABC. b) Tính AH, BH, CH
a) Các hệ thức giữa cạnh và đường cao AH:
\(AH^2=BH.CH\)
\(AB^2=BH.BC\)
\(AC^2=CH.BC\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(AH.BC=AB.AC\)
b) Áp dụng HTL trong tam giác ABC vuông tại A có đg cao AH:
\(AH.BC=AB.AC\)
\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4,8\left(cm\right)\)
Ta có: \(AB^2=BH.BC\)
\(\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
\(BC=CH+BH\)
\(\Rightarrow CH=BC-BH=10-3,6=6,4\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH . Biết BH=10cm; CH=42cm. Tính độ dài của vectơ AB
câu 1:Cho tam giác ABC,vuông tại A,đường cáo AH(H thuộc BC).Biết AB12CM,Ac5cm.tính BH,CHCâu 2:cho tam giác ABC vuông tại A,đường cáo AH(H thuộc BC).Biết AB18cm,BH6cm.tính đô dài các cạnh AB,ACCâu 3:cho tam giac abc vuông tại a,biết ab-3cm,ac4cm,a.tinh bcb:kẻ đường cao ah,tính bhCâu 4:cho tam giác ABC Vuông tại A,biết ab4cm,đường cao ah2cm.Tính các góc và các cạnh còn lại của tam giác
Đọc tiếp
câu 1:Cho tam giác ABC,vuông tại A,đường cáo AH(H thuộc BC).Biết AB=12CM,Ac=5cm.tính BH,CH
Câu 2:cho tam giác ABC vuông tại A,đường cáo AH(H thuộc BC).Biết AB=18cm,BH=6cm.tính đô dài các cạnh AB,AC
Câu 3:cho tam giac abc vuông tại a,biết ab-3cm,ac=4cm,
a.tinh bc
b:kẻ đường cao ah,tính bh
Câu 4:cho tam giác ABC Vuông tại A,biết ab=4cm,đường cao ah=2cm.Tính các góc và các cạnh còn lại của tam giác
Câu 1:
Áp dụng đ/lí pytago vào tam giác ABC vuông tại A CÓ:AB^2+AB^2=BC^2
Hay: 12^2+5^2=169=BC^2
=> BC=13cm
ÁP dụng hệ thức ta có:
+) AB^2=BH.BC
Hay: BH=AB^2:BC=144:13 =144/13(cm)
Ta có CH=BC-BH=13-144/13=25/13(cm)
Đúng 0
Bình luận (0)
Bạn chỉ cần áp dụng hệ thức lượng là đc rồi o0o
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , đường cao AH . Chứng minh rằng 1/AH^2=1/AB^2+1/ac^2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A có AC=10cm, AB=8cm. AH là đường cao. Tính cạnh BC, BH, BH, AH
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=164\)
hay \(BC=2\sqrt{41}cm\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{32\sqrt{41}}{41}cm\\CH=\dfrac{50\sqrt{41}}{41}cm\\AH=\dfrac{40\sqrt{41}}{41}cm\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết \(\dfrac{AB}{AC}\)=\(\dfrac{3}{7}\) và đường cao AH=42cm. Tính BH, HC
Ta có: \(\dfrac{AB}{AC}=\dfrac{3}{7}\)
nên \(AB=\dfrac{3}{7}AC\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{\left(\dfrac{3}{7}AC\right)^2}+\dfrac{1}{AC^2}=\dfrac{1}{42^2}\)
\(\Leftrightarrow\dfrac{1}{\dfrac{9}{49}AC^2}+\dfrac{\dfrac{9}{49}}{\dfrac{9}{49}AC^2}=\dfrac{1}{1764}\)
\(\Leftrightarrow AC^2\cdot\dfrac{9}{49}=2088\)
\(\Leftrightarrow AC^2=11368\)
\(\Leftrightarrow AC=14\sqrt{58}\left(cm\right)\)
\(\Leftrightarrow AB=\dfrac{3}{7}\cdot14\sqrt{58}=6\sqrt{58}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=\left(6\sqrt{58}\right)^2+\left(14\sqrt{58}\right)^2=13456\)
hay BC=116(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}HB=\dfrac{AB^2}{BC}=\dfrac{\left(6\sqrt{58}\right)^2}{116}=18\left(cm\right)\\CH=\dfrac{AC^2}{CH}=\dfrac{\left(14\sqrt{58}\right)^2}{116}=98\left(cm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)