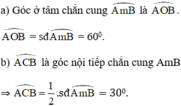Cho hình vẽ, có Bx // MA. Tính góc ACB

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có góc ABC60° a) Tính số đo góc ACB b) Trên tia đối của tia AC lấy điểm D sao cho AD AC. Chứng minh: ΔABDΔABC c) Vẽ tia Bx là tia phân giác của góc ABC. Qua C vẽ đường thắng vuông góc với AC, cắt tia Bx tại E. Chứng minh: ACBE d) Qua D kẻ đường thẳng song song với AB, qua B kẻ đường thẳng song song với AD. Chúng cắt nhau tại H. CM: DH⊥BH.
Đọc tiếp
Cho tam giác ABC vuông tại A có góc ABC=60°
a) Tính số đo góc ACB b) Trên tia đối của tia AC lấy điểm D sao cho AD = AC. Chứng minh:
ΔABD=ΔABC
c) Vẽ tia Bx là tia phân giác của góc ABC. Qua C vẽ đường thắng vuông góc với AC, cắt tia Bx tại E. Chứng minh: AC=BE
d) Qua D kẻ đường thẳng song song với AB, qua B kẻ đường thẳng song song với AD. Chúng cắt nhau tại H. CM: DH⊥BH.
a: \(\widehat{ACB}=30^0\)
b: Xét ΔABD vuông tại A và ΔABC vuông tại A có
AD=AC
AB chung
Do đó: ΔABD=ΔABC
Đúng 0
Bình luận (0)
Cho góc BAD=80. Vẽ tia BX sao cho góc ABC= 100. Tia phân giác của BAD cắt BX tại C.
a. Chứng minh rằng BC//AD
b, Tính số đo của góc ACB
c,Tính tổng BCD với CDA
Cho ∆ABC vuông tại A.Tia phân giác góc ACB cắt AB tại M.Vẽ MD vuông góc với BC tại F.Chứng minh MA = MD (vẽ hình)
Xét ΔCAM vuông tại A và ΔCDM vuông tại D có
CM chung
\(\widehat{ACM}=\widehat{DCM}\)
Do đó: ΔCAM=ΔCDM
Suy ra: MA=MD
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, có góc ABC=6- độ
1. Tính số đo góc ACB
2. Trên tia đối của tia AC lấy điểm M sao cho AM=AC. CM: tia BA là tia p/g của góc MBC
3. Vẽ tia Bx là tia p/g của góc ABC. Qua C vẽ đường thẳng vuông góc với AC cắt Bx tại N. CM: AC=1/2 BN
a, tam giác ABC vuông tại A (gt)
=> góc ABC + góc ACB = 90 (Đl)
góc ABC = 60 (gt)
=> góc ACB = 30
b, xét tam giácCAB và tam giác MAB có : AB chung
AM = AC (gt)
góc CAB = góc MAB = 90
=> tam giác CAB = tam giác MAB (2cgv)
=> góc CBA = góc MBA (đn) mà BA nằm giữa BC và BM
=> BA là pg của góc MBC (đn)
Cho tam giác ABC vuông tại A có góc B= 60o
a) Tính số đo góc ACB
b)Trên tia đối của tia AC lấy điểm D sao cho AD=AC. Chứng minh tam giác ABD= tam gác ABC
c) Vẽ Bx là tia phân giác của góc ABC. Qua C vẽ đường thẳng vuông góc với AC cắt Bx tại E. Chứng minh AC=1/2 BE
Cho tam giác ABC vuông tại A có góc ABC=60 độ
a) Tính số đo góc ACB
b) Trên tia đối của tia AC lấy điểm D sao cho AD=AC. Chứng minh tam giác ABD bằng tam giác ABC
c) Vẽ tia Bx là tia phân giác của góc ABC. Qua C vẽ đường thẳng vuông góc với AC, cắt tia BX tại E. Chứng minh AC=BE:2
a) Xét tam giác vuông ABC, ta có: \(\widehat{ACB}=90^o-\widehat{ABC}=90^o-60^o=30^o\)
b) Ta thấy góc \(\widehat{BAD}\) và \(\widehat{BAC}\) là hai góc kề bù, mà \(\widehat{BAC}=90^o\Rightarrow\widehat{BAD}=90^o\)
Xét hai tam giác vuông ABD và ABC có:
BA chung
DA = CA (gt)
\(\Rightarrow\Delta ABD=\Delta ABC\) (Hai cạnh góc vuông)
c) Do BE là tia phân giác góc ABC nên \(\widehat{ABE}=\widehat{CBE}=30^o\)
Do \(\Delta ABD=\Delta ABC\Rightarrow\hept{\begin{cases}DB=CB\\\widehat{DBA}=\widehat{CBA}=60^o\end{cases}}\)
\(\Rightarrow\widehat{DBE}=\widehat{DBA}+\widehat{ABE}=60^o+30^o=90^o\)
Do BA và CE cùng vuông góc với AC nên BC // CE. Vậy thì \(\widehat{BEC}=\widehat{ABE}=30^o\)
Xét tam giác BCE có: \(\widehat{BEC}=\widehat{CBE}=30^o\) nên nó là tam giác cân. Hay BC = CE
Từ đó ta có : DB = EC
Xét tam giác vuông DBE và ECD có:
DB = EC
DE chung
\(\Rightarrow\Delta DBE=\Delta ECD\) (Cạnh huyền cạnh góc vuông)
\(\Rightarrow BE=CD\)
Mà CD = CA + AD = 2AC
Vậy nên BE = 2AC.
Đúng 1
Bình luận (2)
Ta có : A + B + C = 180o (tổng 3 góc 1 tam giác)
Mà : A = 90o ; B = 60o
Nên : C = 180 - 90 - 60 = 30o
Vậy ACB = 30o
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho góc BAD = 80 độ . vẽ tia Bx sao cho góc ABX = 105 độ . Tia Bx và tia AD cùng thuococj NMP bờ AB . Tia phân giác của góc BAD vắt Bx tại C
a, CMR Bc// AD
b, Tính số đo ACB
c, Tính tổng BCD + ADC ?
Mình cần gaaops !! Ai nhanh mk tick cho Mơn ạ
a)
Vì \(\widehat{ABz}+\widehat{zBC}\) là hai góc kẻ bù
Nên ta có :
=> \(\widehat{ABz}+\widehat{zBC}=180^o\)
Thay số: \(80^o+\widehat{zBC}=180^o\)
\(\Rightarrow\widehat{zBC}=180^o-80^o=100^o\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có góc B= 60o
a) Tính số đo góc ACB
b)Trên tia đối của tia AC lấy điểm D sao cho AD=AC. Chứng minh tam giác ABD= tam gác ABC
c) Vẽ Bx là tia phân giác của góc ABC. Qua C vẽ đường thẳng vuông góc với AC cắt Bx tại E. Chứng minh AC=1/2 BE
a) Ta có tam giác đó vuông tại A nên góc CAB = 90 độ
Mà theo định lý , ta có tổng của ba góc của tam giác luôn luôn bằng 180 độ
=> Góc ACB + góc CAB + góc ABC = 180 độ
<=> Góc ACB + 90 độ + 60 độ = 180 độ
<=> Góc ACB = 180 độ - 60 độ - 90 độ
<=> Góc ACB = 30 độ
b) Ta có diện tích tam giác bằng đáy x chiều cao : 2
Mà đáy AD = AC; cả hai hình cùng có chung chiều cao là từ điểm B kéo xuống vuông góc với CD
=> ABC = ABD
Đúng 0
Bình luận (0)
Ta chứng minh trong một tam giác vuông có một góc bằng \(60^o\) thì cạnh huyền bằng 2 lần cạnh góc vuông đối diện với góc \(30^o\).
Xét tam giác vuông MHP có \(\widehat{H}=90^o,\widehat{P}=60^o\).
Trên tia đối của tia HP lấy điểm N sao cho NH = HP.
Tam giác MNP cân tại M có \(\widehat{P}=60^o\) nên là tam giác đều.
Suy ra \(NP=2HP=MP\). Vì vậy MP = 2HP (đpcm).
Gọi giao điểm của CA và BE là I.
Ta tính được các góc \(\widehat{EIC}=60^o,\widehat{AIB}=60^o\).
Các tam giác vuông CIE và IAB có các góc \(\widehat{EIC}=\widehat{AIB}=60^o\), suy ra \(2CI=EI,BI=2AI\).
Suy ra \(BE=EI+IB=2CI+2IA=2CA\) hay \(AC=\frac{1}{2}BE\).
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có góc B= 60o
a) Tính số đo góc ACB
b)Trên tia đối của tia AC lấy điểm D sao cho AD=AC. Chứng minh tam giác ABD= tam gác ABC
c) Vẽ Bx là tia phân giác của góc ABC. Qua C vẽ đường thẳng vuông góc với AC cắt Bx tại E. Chứng minh AC=1/2 BE
a) Ta có tam giác đó vuông tại A nên góc CAB = 90 độ
Mà theo định lý , ta có tổng của ba góc của tam giác luôn luôn bằng 180 độ
=> Góc ACB + góc CAB + góc ABC = 180 độ
<=> Góc ACB + 90 độ + 60 độ = 180 độ
<=> Góc ACB = 180 độ - 60 độ - 90 độ
<=> Góc ACB = 30 độ
b) Ta có diện tích tam giác bằng đáy x chiều cao : 2
Mà đáy AD = AC; cả hai hình cùng có chung chiều cao là từ điểm B kéo xuống vuông góc với CD
=> ABC = ABD
Câu c ngày mai mình giải nhé
Đúng 0
Bình luận (0)
a) Ta có tam giác đó vuông tại A nên góc CAB = 90 độ
Mà theo định lý , ta có tổng của ba góc của tam giác luôn luôn bằng 180 độ
=> Góc ACB + góc CAB + góc ABC = 180 độ
<=> Góc ACB + 90 độ + 60 độ = 180 độ
<=> Góc ACB = 180 độ - 60 độ - 90 độ
<=> Góc ACB = 30 độ
b) Ta có diện tích tam giác bằng đáy x chiều cao : 2
Mà đáy AD = AC; cả hai hình cùng có chung chiều cao là từ điểm B kéo xuống vuông góc với CD
=> ABC = ABD
chúc cậu hok tốt @_@
Đúng 0
Bình luận (0)
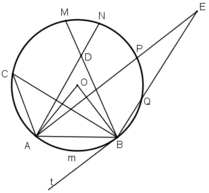
Trong hình 67, cung AmB có số đo là
60
°
. Hãy:a) Vẽ góc ở tâm chắn cung AmB. Tính góc AOB.b) Vẽ góc nội tiếp đỉnh C chắn cung AmB. Tính góc ACB.c) Vẽ góc tạo bởi tia tiếp tuyến Bt và dây cung BA. Tính góc ABt.d) Vẽ góc ADB có đỉnh D ở bên trong đường tròn. So sánh
ADB và ACB
e) Vẽ góc AEB có đỉnh E ở bên ngoài đường tròn (E và C cùng phía đối với AB). So sánh cung AEB với cung ACB
Đọc tiếp
Trong hình 67, cung AmB có số đo là 60 ° . Hãy:
a) Vẽ góc ở tâm chắn cung AmB. Tính góc AOB.
b) Vẽ góc nội tiếp đỉnh C chắn cung AmB. Tính góc ACB.
c) Vẽ góc tạo bởi tia tiếp tuyến Bt và dây cung BA. Tính góc ABt.
d) Vẽ góc ADB có đỉnh D ở bên trong đường tròn. So sánh ADB và ACB
e) Vẽ góc AEB có đỉnh E ở bên ngoài đường tròn (E và C cùng phía đối với AB). So sánh cung AEB với cung ACB