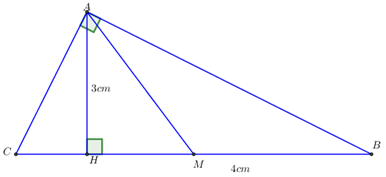
Cho tam giác nhọn ABC (AB < AC), đường cao AH và đường trung tuyến AM. CMR HC – HB = 2HM

Những câu hỏi liên quan
Cho tam giác nhọn ABC, góc B> góc C, đường cao AH và đường trung tuyến AM.
a) CMR: HC-HB=2HM
b) Gọi a là góc tạo bởi đường cao và đường trung tuyến. CMR: \(\tan\alpha=\frac{\cot C-\cot B}{2}\)
a) Do AM là trung tuyến nên BM = MC
Ta có : \(HC-HB-2HM\)
\(=HM+MC-HB-HM-HM\)
\(=MC-HB-HM\)
\(=MC-\left(HB+HM\right)\)
\(=MC-MB=0\)
\(\Rightarrow HC-HB=2MC\left(đpcm\right)\)
b) Xét \(\Delta AHM\)có \(\tan a=\frac{HM}{AH}\)
Xét \(\Delta AHC\)có \(\cot C=\frac{HC}{AH}\)
Xét \(\Delta AHB\)có \(\cot B=\frac{HB}{AH}\)
Ta có : \(\frac{\cot C-\cot B}{2}=\left(\frac{HC}{AH}-\frac{HB}{AH}\right)\div2=\frac{HC-HB}{AH}\div2\)
Mà \(HC-HB=2HM\)( câu a )
\(\Rightarrow\frac{\cot C-\cot B}{2}=\frac{2HM}{AH}\div2=\frac{HM}{AH}=\tan a\left(đpcm\right)\)
Vậy ...
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC, góc B góc C, đường cao AH và đường trung tuyến AM. a CMR HC HB 2HMb Gọi a là góc tạo bởi đường cao và đường trung tuyến. CMR tanα cotC−cotB2
cho tam giác abc nhọn ab<ac đường cao AH=h đường trung tuyến AM biết góc HAM=∝ cmr
a) HC-HB=2h.tan∝
b) tan∝=cosC/2-cosB/2
giải giúp mk với
Bài 6 : Độ dài 2 đường chéo của 1 tứ giác là 9 cm, 13 cm, độ dài góc xem giữa 2 đường chéo là 45 độ. Tính S tứ giác?
Bài 7 :cho tam giác ABC nhọn, gócB>gócC. Đường cao AH, trung tuyến AM.
cmr: a HB-HC=2HM
b Gọi anfa là góc tạo bởi đường cao và trung tuyến, cm : tan anfa=( cot C - cotB ) Chia 2 .
Cho tam giác ABC nhọn ( AB<AC ) , đường cao AH , trung tuyến AM . C/m HC - HB = 2 HM
cho tam giác abc vuông tại a , trung tuyến AM = 2,5 , đường cao AH . Biết AB/BC = 0,8 . tính AB , AC,BC,HC,HB,HA
ΔABC vuông tại A có AM là trung tuyến
nên BC=2*AM
=>BC=5
AB/BC=4/5
=>AB/5=4/5
=>AB=4
AC=căn 5^2-4^2=3
ΔABC vuông tại A có AH là đường cao
nên BH*BC=BA^2; CH*CB=CA^2
=>BH=4^2/5=3,2cm; CH=3^2/5=1,8cm
ΔABC vuông tại A có AH là đường cao
nên AH*BC=AB*AC
=>AH*5=4*3=12
=>AH=2,4cm
Đúng 1
Bình luận (0)
cho tam giác ABC có AB<AC . phân giác AD trung tuyến AM, đường cao AH
a) so sánh HB và HC
b) CMR góc HAC> A/2
c) nhận xét gì về vị trí các tia AH, AD, AM
Cho tam giác ABC vuông tại A có đường cao AH và đường trung tuyến AM. Biết AH=3cm; HB=4cm. Hãy tính AB,AC,AM và diện tích tam giác ABC
\(HC=\dfrac{3^2}{4}=2.25\left(cm\right)\)
BC=HB+HC=6,25(cm)
AM=BC/2=3,125(cm)
\(AB=\sqrt{4\cdot6.25}=5\left(cm\right)\)
\(AC=\sqrt{6.25^2-5^2}=3.75\left(cm\right)\)
Đúng 4
Bình luận (0)
+ ) áp dụng định lí Pytago trong tam giác vuông \(ABH\) vuông tại \(H\) , ta có :
\(AB^2=AH^2+HB^2=3^2+4^2=25\Rightarrow AB=5\left(cm\right)\)
+ ) áp dụng hệ thức về cạnh và đường cao trong tam giác vuông \(ABC\) với \(AH\) là đường cao , ta có :
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\) \(\dfrac{1}{AC^2}=\dfrac{1}{AH^2}-\dfrac{1}{AB^2}\)
\(\Leftrightarrow\) \(\dfrac{1}{AC^2}=\dfrac{1}{3^2}-\dfrac{1}{5^2}=\dfrac{16}{225}\)
\(\Rightarrow AC=\dfrac{15}{4}\left(cm\right)\)
+ ) áp dụng định lí Pytago trong tam giác vuông \(ABC\) vuông tại \(A\) , ta có :
\(BC^2=AB^2+AC^2=5^2+\left(\dfrac{15}{4}\right)^2=\dfrac{625}{16}\)
\(\Rightarrow BC=\dfrac{25}{4}\left(cm\right)\)
+ ) tam giác \(ABC\) vuông tại \(A\) có trung tuyến \(AM\) nên ta có :
\(AM=\dfrac{1}{2}BC=\dfrac{25}{8}\left(cm\right)\)
Đúng 2
Bình luận (1)
Cho tam giác ABC vuông tại A có đường cao AH và đường trung tuyến AM .Biết AH = 3cm, HB = 4 cm. Hãy tính AB AC AM , và diện tích tam giác ABC .
Xét tam giác ABH vuông tại H, ta có:
\(AB^2=AH^2+BH^2\)\(=3^2+4^2=25\)
\(\Rightarrow AB=5\left(cm\right)\)
Xét tam giác ABC vuông tại A, theo hệ thức lượng ta có:
\(AH^2=AB\cdot AC\Rightarrow AC=\dfrac{AH^2}{AB}=\dfrac{3^2}{5}=1,8\left(cm\right)\)
Do đó:\(BC=\sqrt{AB^2+AC^2}=\sqrt{5^2+1,8^2}\simeq5,3\left(cm\right)\)
AM là đường trung tuyến trong tam giác vuông ABC
=> AM=\(\dfrac{1}{2}\) BC= 2,65 \(\left(cm\right)\)
Đúng 0
Bình luận (0)