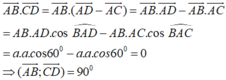Cho hthoi ABCD có BAC=60* và AB=1. Tính AC

Những câu hỏi liên quan
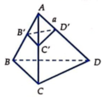
Cho tứ diện ABCD có
A
B
A
C
A
D
a
;
B
A
C
60
°
;
C
A
D
60
°
;
D
A
B
90
°
. Khoảng cách giữa hai đường thẳng AC và BD là A.
a
30
10...
Đọc tiếp
Cho tứ diện ABCD có A B = A C = A D = a ; B A C = 60 ° ; C A D = 60 ° ; D A B = 90 ° . Khoảng cách giữa hai đường thẳng AC và BD là
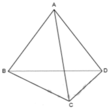
A. a 30 10
B. a 2
C. a 3 2
D. a 2 2
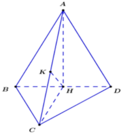
Ta có:

Xét ∆ A H C vuông tại H có đường cao KH ta có:
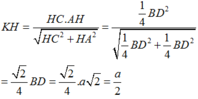
Chọn B.
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có
A
B
A
C
A
D
và
B
A
C
^
B
A
D
^
60
°
. Xác định góc giữa hai đường thẳng AB và CD A.
90
°
B...
Đọc tiếp
Cho tứ diện ABCD có A B = A C = A D và B A C ^ = B A D ^ = 60 ° . Xác định góc giữa hai đường thẳng AB và CD
A. 90 °
B. 45 °
C. 60 °
D. 30 °
Cho tứ diện ABCD có ABACAD và
B
A
C
^
B
A
D
^
60
°
. Xác định góc giữa hai đường thẳng AB và CD
Đọc tiếp
Cho tứ diện ABCD có AB=AC=AD và B A C ^ = B A D ^ = 60 ° . Xác định góc giữa hai đường thẳng AB và CD
![]()
![]()
![]()
![]()
Cho tứ diện ABCD có
A
B
A
C
A
D
1
,
B
A
C
^
60
∘
,
B
A
D
^
90
∘
,
D
A
C...
Đọc tiếp
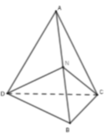
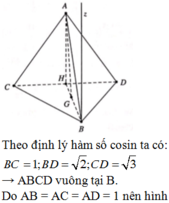
Cho tứ diện ABCD có A B = A C = A D = 1 , B A C ^ = 60 ∘ , B A D ^ = 90 ∘ , D A C ^ = 120 ∘ Tính cosin của góc tạo bởi hai đường thẳng AG và CD, trong đó G là trọng tâm tam giác BCD.
A. 1 6
B. 1/3
C. 1/6
D. 1 3
Cho tứ diện ABCD có ABACADvà
B
A
C
B
A
D
60
°
. Xác định góc giữa hai đường thẳng AB và CD A.
90
°
B.
45
°
C.
60
°
D.
30
°
Đọc tiếp
Cho tứ diện ABCD có AB=AC=ADvà B A C = B A D = 60 ° . Xác định góc giữa hai đường thẳng AB và CD
A. 90 °
B. 45 °
C. 60 °
D. 30 °
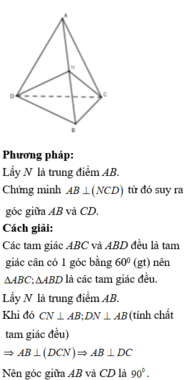
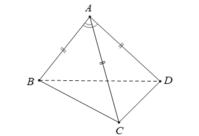
Các tam giác ABC và ABD đều là tam giác cân có 1 góc bằng 600 (gt) nên ∆ A B C ; ∆ A B D là các tam giác đều.
Lấy N là trung điểm AB. Khi đó C N ⊥ A B ; D N ⊥ A B (tính chất tam giác đều)
⇒ A B ⊥ D C N ⇒ A B ⊥ D C
Nên góc giữa AB và CD là 90 ° .
Chọn đáp án A.
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có AB AC AD a và
B
A
C
^
B
A
D
^
60
°
. Hãy xác định góc giữa cặp vectơ
A
B
→
,
C
D
→
A.
60
°
B.
45
°
C. ...
Đọc tiếp
Cho tứ diện ABCD có AB = AC = AD = a và B A C ^ = B A D ^ = 60 ° . Hãy xác định góc giữa cặp vectơ A B → , C D →
A. 60 °
B. 45 °
C. 120 °
D. 90 °
Cho hình thoi ABCD có góc BAC=60*, cạnh AB=1. Độ dài của véc tơ AC là bnhiu?
Cho tứ diện ABCD có AB 3, AC 2, AD 6,
B
A
C
^
90
°
,
C
A
D
^
120
°
,
B
A
D
^
...
Đọc tiếp
Cho tứ diện ABCD có AB = 3, AC = 2, AD = 6, B A C ^ = 90 ° , C A D ^ = 120 ° , B A D ^ = 60 ° . Thể tích khối tứ diện ABCD bằng
A. 6 2
B. 2 2 3
C. 2
D. 3 2
Đáp án D
Phương pháp
Sử dụng công thức tính nhanh thể tích khối tứ diện biết ba cạnh và ba góc cùng xuất phát từ một đỉnh:
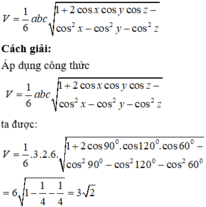
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có AB 3a, AC 5a, AD 4a, các góc
B
A
C
^
D
A
C
^
B
A
D
^
60
°
. Khi đó thể tích khối ABCD là: A.
5
a
3
3
B...
Đọc tiếp
Cho tứ diện ABCD có AB = 3a, AC = 5a, AD = 4a, các góc B A C ^ = D A C ^ = B A D ^ = 60 ° . Khi đó thể tích khối ABCD là:
A. 5 a 3 3
B. 5 a 3 2
C. a 3 2
D. 10 a 3 2