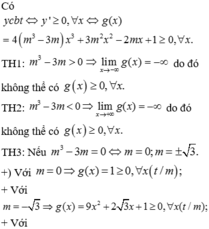1/3x3+mx2+(3m-2)x+1 đồng biến trên (1;2)

Những câu hỏi liên quan
Tìm m để hàm số y đồng biến trên R
a, y = mx - x2 - 2x + mx2 + m
b, (m2 - 3m +2).x2 + (m - 1).x + \(\sqrt{3}\)
Lời giải:
a. $y=mx-x^2-2x+mx^2+m=x^2(m-1)+x(m-2)+m$
Lấy $x_1,x_2\in R$ sao cho $x_1\neq x_2$
$y(x_1)=x_1^2(m-1)+x_1(m-2)+m$
$y(x_2)=x_2^2(m-1)+x_2(m-2)+m$
Để hàm đồng biến thì:
$\frac{y(x_1)-y(x_2)}{x_1-x_2}>0$
$\Leftrightarrow \frac{x_1^2(m-1)+x_1(m-2)+m-[x_2^2(m-1)+x_2(m-2)+m]}{x_1-x_2}>0$
$\Leftrightarrow \frac{(m-1)(x_1^2-x_2^2)+(m-2)(x_1-x_2)}{x_1-x_2}>0$
$\Leftrightarrow (m-1)(x_1+x_2)+(m-2)>0$
Với mọi $x_1,x_2\in\mathbb{R}$ thì không có cơ sở để tìm $m$ sao cho hàm đồng biến.
b.
Xét tương tự câu 1, với $x_1\neq x_2\in \mathbb{R}$ thì hàm đồng biến khi:
$(m^2-3m+2)(x_1+x_2)+(m-1)>0$
Với mọi $x_1, x_2\in\mathbb{R}$ thì điều này xảy ra khi:
$m^2-3m+2=0$ và $m-1>0$
$\Leftrightarrow (m-1)(m-2)=0$ và $m-1>0$
$\Leftrightarrow m=2$
Đúng 2
Bình luận (0)
Tìm tập hợp tất cả các tham số m để hàm số
y
x
3
–
m
x
2
+
(
m
–
1
)
x
+
1
đồng biến trên khoảng (1; 2) A.
m
≤
11
3
B. m
11
3
C.
m
≤
2
D. m 2
Đọc tiếp
Tìm tập hợp tất cả các tham số m để hàm số y = x 3 – m x 2 + ( m – 1 ) x + 1 đồng biến trên khoảng (1; 2)
A. m ≤ 11 3
B. m < 11 3
C. m ≤ 2
D. m < 2
Có bao nhiêu số thực m để hàm số
y
m
3
-
3
m
x
4
+
m
2
x
3
-
m
x
2
+
x
+
1
đồng biến trên khoảng
-
∞...
Đọc tiếp
Có bao nhiêu số thực m để hàm số y = m 3 - 3 m x 4 + m 2 x 3 - m x 2 + x + 1 đồng biến trên khoảng - ∞ ; + ∞
A. 3
B. 1
C. Vô số
D. 2
Có bao nhiêu số thực m để hàm số
y
m
3
-
3
m
x
4
+
m
2
x
3
-
m...
Đọc tiếp
Có bao nhiêu số thực m để hàm số y = m 3 - 3 m x 4 + m 2 x 3 - m x 2 + x + 1 đồng biến trên khoảng - ∞ ; + ∞
A. 3
B. 1
C. Vô số
D. 2
Chọn đáp án A.
![]()
![]()
![]()
do đó không thể có g x ≥ 0 , ∀ x
![]()
do đó không thể có g x ≥ 0 , ∀ x
![]()
+) Với m = 0 ⇒ g ( x ) = 1 ≥ 0 , ∀ x ( t / m )
+ Với m = - 3 ⇒ g ( x ) = 9 x 2 + 2 x 3 + 1 ≥ 0 , ∀ x ( t / m )
+ Với m = 3 ⇒ g ( x ) = 9 x 2 - 2 x 3 + 1 ≥ 0 , ∀ x ( t / m )
Vậy tất cả các giá trị cần tìm là m ∈ 0 ; 3 ; - 3
*Một cách tương tự điều kiện cần để một đa thức bậc lẻ
![]()
là a 2 n + 1 = 0
Đúng 0
Bình luận (0)
Cho hàm số
y
−
1
3
x
3
+
m
x
2
+
3
m
+
2
x
+
1.
Tìm tất cả các giá tị của m để hàm số nghịch biến trên R A.
m
−
1...
Đọc tiếp
Cho hàm số y = − 1 3 x 3 + m x 2 + 3 m + 2 x + 1. Tìm tất cả các giá tị của m để hàm số nghịch biến trên R
A. m > − 1 m < − 2
B. − 2 ≤ m ≤ − 1.
C. m ≥ − 1 m ≤ − 2
D. − 2 < m < − 1.
Đáp án B
y ' = − x 2 + 2 mx+ ( 3 m+ 2 )
Hàm số nghịch biến trên R ⇔ y ' ≤ 0 moị x
⇔ a< 0 Δ y ' ' ≤ 0 ⇔ − 1 < 0 m 2 + 3 m+ 2 ≤ 0 ⇔ − 2 ≤ m ≤ − 1
Đúng 0
Bình luận (0)
Cho hàm số
y
−
1
3
x
3
+
m
x
2
+
3
m
+
2
x
+
1.
Tìm tất cả các giá tị của m để hàm số nghịch biến trên R A.
m
−
1...
Đọc tiếp
Cho hàm số y = − 1 3 x 3 + m x 2 + 3 m + 2 x + 1. Tìm tất cả các giá tị của m để hàm số nghịch biến trên R
A. m > − 1 m < − 2
B. − 2 ≤ m ≤ − 1.
C. m ≥ − 1 m ≤ − 2
D. − 2 < m < − 1.
Đáp án B
y ' = − x 2 + 2 mx+ ( 3 m+ 2 )
Hàm số nghịch biến trên R ⇔ y ' ≤ 0 moị x
⇔ a< 0 Δ y ' ' ≤ 0 ⇔ − 1 < 0 m 2 + 3 m+ 2 ≤ 0 ⇔ − 2 ≤ m ≤ − 1
Đúng 0
Bình luận (0)
1) hàm số \(y=\dfrac{x+m^2}{x+4}\) đồng biến trên từng khoảng xác định
2) hàm số \(y=\dfrac{x+2}{x+3m}\) đồng biến trên khoảng (\(-\infty\),-6)
1: TXĐ: D=R\{-4}
\(y=\dfrac{x+m^2}{x+4}\)
=>\(y'=\dfrac{\left(x+m^2\right)'\left(x+4\right)-\left(x+m^2\right)\left(x+4\right)'}{\left(x+4\right)^2}\)
\(=\dfrac{x+4-x-m^2}{\left(x+4\right)^2}=\dfrac{4-m^2}{\left(x+4\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định thì
\(\dfrac{4-m^2}{\left(x+4\right)^2}>0\forall x\in TXĐ\)
=>\(4-m^2>0\)
=>\(m^2< 4\)
=>-2<m<2
Đúng 1
Bình luận (0)
định m để hàm số y=1/3x3 -2x2+mx-2 đồng biến trên tập xác định
Một học sinh giải bài toán “Tìm tất cả các giá trị thực của tham số m sao cho hàm số
y
m
x
3
+
m
x
2
+
m
−
2
x
+
10
đồng biến trên i” theo các bước như sau:Bước 1: Hàm số xác định trên i, và
y
3
m
x...
Đọc tiếp
Một học sinh giải bài toán “Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m x 3 + m x 2 + m − 2 x + 10 đồng biến trên i” theo các bước như sau:
Bước 1: Hàm số xác định trên i, và y ' = 3 m x 2 + 2 m x + m − 2
Bước 2: Yêu cầu bài toán tương đương với y ' > 0, ∀ x ∈ ℝ ⇔ 3 m x 2 + 2 m x + m − 2 > 0, ∀ x ∈ ℝ
Bước 3: ⇔ a = 3 m > 0 Δ ' = 6 m − 2 m 2 < 0 ⇔ m < 0 m > 3 m > 0
Bước 4: ⇔ m > 3. Vậy m>3
Hỏi học sinh này đã bắt đầu sai ở bước nào?
A. Bước 2
B. Bước 3
C. Bước 1
D. Bước 4
Đáp án B
Để ý thấy lời giải bài toán sai ở bước 3 do m có thể nhỏ hơn 0
Đúng 0
Bình luận (0)
Cho hàm số x2-2(m-1)x+1-3m. Tìm m để hàm số đồng biến trên (2, +∞) ?