giúp e câu 3 ạ


 giúp e câu 4,5 vs ạ xem giúp e câu 3 vậy đc chưa ạ ? 🤧
giúp e câu 4,5 vs ạ xem giúp e câu 3 vậy đc chưa ạ ? 🤧
Về câu 3 mình cảm thấy bạn trả lời ổn rồi.
Câu 4:
Chủ đề của bài thơ: tình cảm gia đình ( cụ thể với người mẹ ).
Câu 5:
Qua đoạn thơ trên em cảm nhận được tình yêu thương sâu sâu sắc và nỗi nhớ của tác giả đối với người mẹ của mình. Hồi tưởng về quá khứ, hình ảnh tác giả nhớ nhất chính là người mẹ. Nét cười đen nhánh, hình dáng của mẹ chưa xóa mờ trong kí ức. Tất cả đều chứa chan nỗi nhớ về hình ảnh mẹ thuở xưa kia. Qua đó,ta thấy được giá trị đạo đức cao đẹp của người Việt Nam, đó là tình cảm gia đình thiêng liêng, sâu sắc.
Anh chị giúp e câu 3 và câu 4 với ạ. E cảm ơn
Giúp e làm các câu đó đi ạ trừ câu 3, 4 ra thôi ạ


giúp e câu 3 với ạ
Giúp e câu 3 với ạ

Giúp e câu 3 với ạ
a. BPT đã cho vô nghiệm khi:
\(f\left(x\right)\ge0\) nghiệm đúng với mọi x
\(\Leftrightarrow\left\{{}\begin{matrix}a=1>0\\\Delta'=\left(m+2\right)^2-\left(3m^2+5m-8\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow-2m^2-m+12\le0\) \(\Rightarrow\left[{}\begin{matrix}m\ge\dfrac{-1+\sqrt{97}}{4}\\m\le\dfrac{-1-\sqrt{97}}{4}\end{matrix}\right.\)
b.
\(f\left(x\right)=0\) có 2 nghiệm pb
\(\Leftrightarrow\Delta'=-2m^2-m+12>0\)
\(\Leftrightarrow\dfrac{-1-\sqrt{97}}{4}< m< \dfrac{-1+\sqrt{97}}{4}\)
giúp em câu 3 e ạ ;-;
Giúp e câu 3 đi ạ
\(d\left(M;\left(ABCD\right)\right)=\dfrac{1}{2}d\left(S;\left(ABCD\right)\right)=\dfrac{a}{2}\)
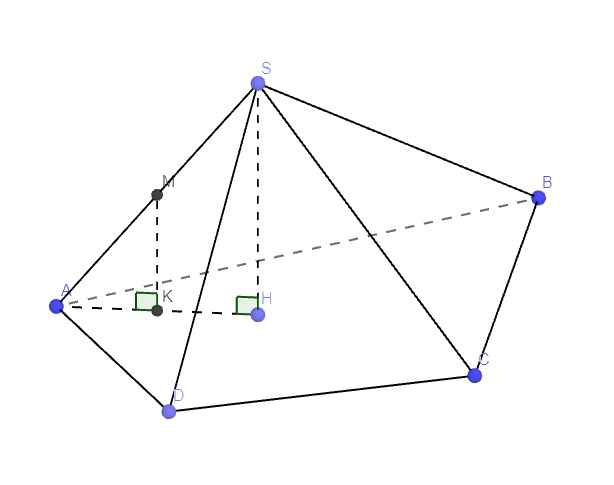
Theo định lý Talet ta luôn có:
\(\dfrac{MK}{SH}=\dfrac{AM}{SA}=\dfrac{1}{2}\Rightarrow MK=\dfrac{1}{2}SH\)
Hay \(d\left(M;\left(ABCD\right)\right)=\dfrac{1}{2}d\left(S;\left(ABCD\right)\right)\)
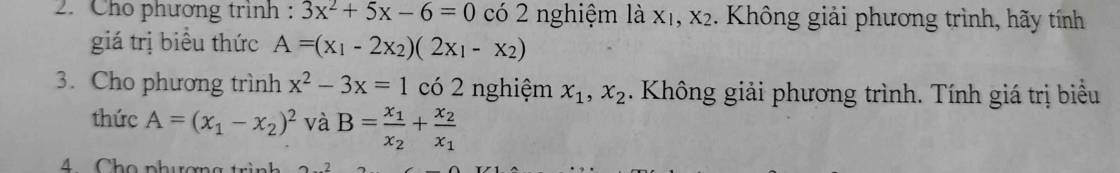 Giúp e câu 3 với ạ
Giúp e câu 3 với ạ
\(x^2-3x=1\Leftrightarrow x^2-3x-1=0\)
Theo Vi - ét, ta có :
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=1\\x_1x_2=\dfrac{c}{a}=-1\end{matrix}\right.\)
\(A=\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2\)
\(=1^2-4.\left(-1\right)\)
\(=5\)
\(B=\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}=\dfrac{x_1^2+x_2^2}{x_1x_2}=\dfrac{\left(x_1+x_2\right)^2-2x_1x_2}{x_1x_2}=\dfrac{1^2-2.\left(-1\right)}{\left(-1\right)}=-4\)