Tìm m biết C(x) = (m-4)\(x^6\) - 7\(x^5+2x^3+2m+25\) có hệ số tự do là\(\sqrt{9}\)

Những câu hỏi liên quan
Bài 1: Tìm m để các hàm số sau là hàm số bậc nhất a) y ( m - 2 )x - dfrac{2}{3} b) y ( 4 - 2022m )x - 2 c) y sqrt{1-2m}x + m - 3Bài 2: Cho đồ thị hàm số y -2x + 3a) Xác định hệ số a,bb) Các điểm A( -2 ; 7) ; B(sqrt{2} ; 6)c) Tìm tọa độ điểm M thuộc ( d ) có tung độ 11d) Tìm tọa độ điểm C thuộc ( d ), biết rằng hoành độ của điểm C gấp 3 tung độ của nóe) Tìm tọa độ điểm E thuộc ( d ), biết rằng tung độ của điểm E và hoành độ là 2 số đối nhau
Đọc tiếp
Bài 1: Tìm m để các hàm số sau là hàm số bậc nhất
a) y= ( m - 2 )x - \(\dfrac{2}{3}\) b) y= ( 4 - 2022m )x - 2 c) y= \(\sqrt{1-2m}\)x + m - 3
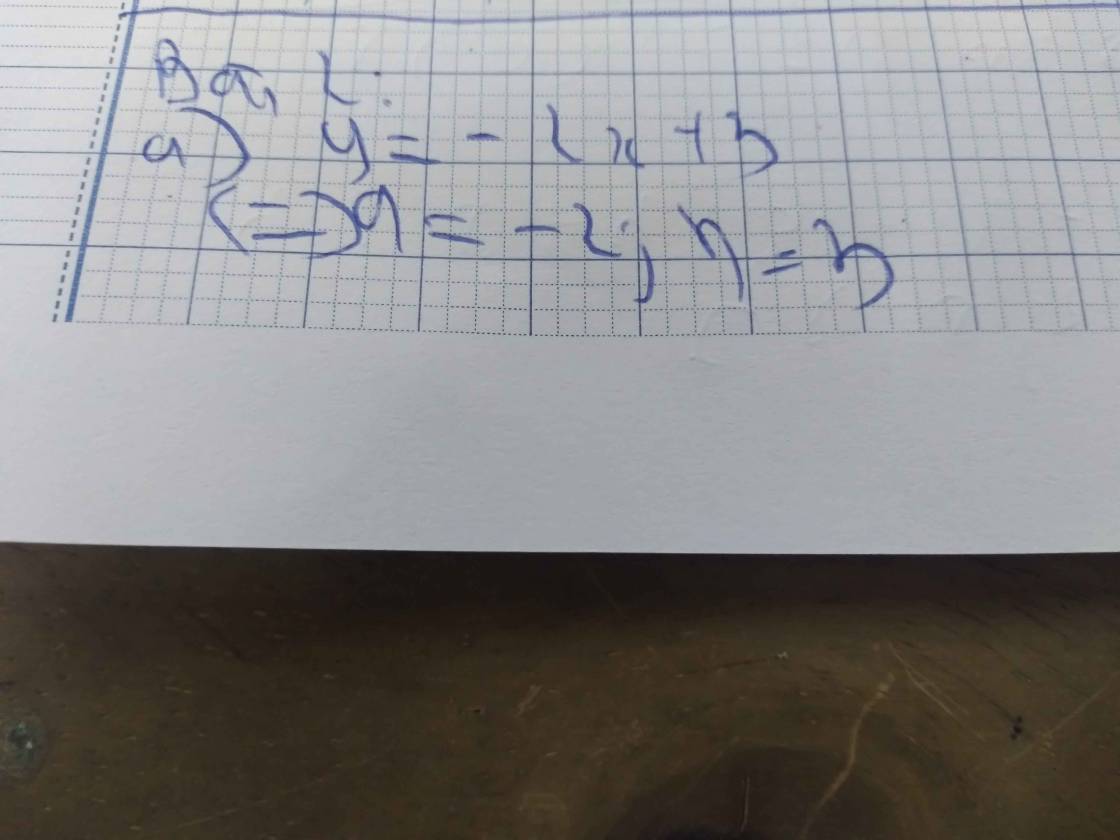
Bài 2: Cho đồ thị hàm số y= -2x + 3
a) Xác định hệ số a,b
b) Các điểm A( -2 ; 7) ; B(\(\sqrt{2}\) ; 6)
c) Tìm tọa độ điểm M thuộc ( d ) có tung độ = 11
d) Tìm tọa độ điểm C thuộc ( d ), biết rằng hoành độ của điểm C gấp 3 tung độ của nó
e) Tìm tọa độ điểm E thuộc ( d ), biết rằng tung độ của điểm E và hoành độ là 2 số đối nhau
thu gọn sắp xếp theo lũy thừa giảm dần của biến rồi tìm bậc , tìm hệ số cao nhất , hệ số tự do của mỗi đa thức sau
a, 5x^2 - 7 + 6 x - 8x^3 - x^4 - 2x^2 + 4x^3
b, x^4 + 5 - 8x^3 - 5x^2 +3x^3 - 2x^4
c, -6x^3 + 5 x - 1 + 2x^2 + 6x^3 - 2x +5x^2
d, 5x^4 - 3x^2 + 9 x^3 - 2^4 + 4 + 5x
Lời giải:
Các đa thức sau khi được thu gọn và sáp xếp theo lũy giảm dần:
a) \(-x^4-4x^3+3x^2+6x-7\)
Bậc của đa thức: 4
Hệ số cao nhất : -1
Hệ số tự do : -7
b) \(-x^4-5x^3-5x^2+5\)
Bậc của đa thức: 4
Hệ số cao nhất : -1
Hệ số tự do: 5
c) \(7x^2+3x-1\)
Bậc của đa thức: 2
Hệ số cao nhất: 7
Hệ tự do: -1
d) \(3x^4+9x^3-3x^2+5x+4\)
Bậc của đa thức: 4
Hệ số cao nhất: 3
Hệ số tự do: 4
Đúng 0
Bình luận (0)
1. Giải phương trình:1/ sqrt{x-4}+sqrt{6-x}x^2-10x+272/ sqrt{x^2-6x+9}+sqrt{x^2-10x+25}83/ y^2-2y+3dfrac{6}{x^2+2x+4}4/ x^2-x-42sqrt{x-1}left(1-xright)5/ x^2-left(m+1right)x+2m-606/ 615+x^22^y2.a, Cho các số dương a,b thoả mãn a+b2ab.Tính GTLN của biểu thức Qdfrac{2}{sqrt{a^2+b^2}}.b, Cho các số thực x,y thoả mãn x-sqrt{y+6}sqrt{x+6}-y.Tính GTNN và GTLN của biểu thức Px+y.3. Cho hàm số yleft(m+3right)x+2m-10 có đồ thị đường thẳng (d), hàm số yleft(m-4right)x-2m-8 có đồ thị đường thẳng (d2) (m là...
Đọc tiếp
1. Giải phương trình:
1/ \(\sqrt{x-4}+\sqrt{6-x}=x^2-10x+27\)
2/ \(\sqrt{x^2-6x+9}+\sqrt{x^2-10x+25}=8\)
3/ \(y^2-2y+3=\dfrac{6}{x^2+2x+4}\)
4/ \(x^2-x-4=2\sqrt{x-1}\left(1-x\right)\)
5/ \(x^2-\left(m+1\right)x+2m-6=0\)
6/ \(615+x^2=2^y\)
2.
a, Cho các số dương a,b thoả mãn \(a+b=2ab\).
Tính GTLN của biểu thức \(Q=\dfrac{2}{\sqrt{a^2+b^2}}\).
b, Cho các số thực x,y thoả mãn \(x-\sqrt{y+6}=\sqrt{x+6}-y\).
Tính GTNN và GTLN của biểu thức \(P=x+y\).
3. Cho hàm số \(y=\left(m+3\right)x+2m-10\) có đồ thị đường thẳng (d), hàm số \(y=\left(m-4\right)x-2m-8\) có đồ thị đường thẳng (d2) (m là tham số, \(m\ne-3\) và \(m\ne4\)). Trên mặt phẳng toạ độ Oxy, (d) cắt trục hoành tại điểm A, (d2) cắt trục hoành tại điểm B, (d) cắt (d2) tại điểm C nằm trên trục tung. Chứng minh hệ thức \(\dfrac{OA}{BC}=\dfrac{OB}{AC}\).
4. Cho 2 đường tròn (O) và (I) cắt nhau tại dây AB, chứng minh rằng \(\Delta OAI=\Delta OBI\).
Cho 2 đa thức: F(x)= (2x2 -4x + 5) - (x2 - 6) + 2x-3
G(x)= -x2 - 2x - 9
a) Thu gọn F(x) và cho biết hệ số tự do, hệ số bậc 1 của F(x)
b) Tìm M(x)= F(x) +G(x) ; N(x)=F(x) - G(x)
c) Tìm nghiệm của M(x); N(x)
d) TÌM x để F(x) = x2 - 3
a) \(F\left(x\right)=\left(2x^2-4x+5\right)-\left(x^2-6\right)+2x-3\)
\(=2x^2-4x+5-x^2+6+2x-3\)
\(=\left(2x^2-x^2\right)+\left(2x-4x\right)+\left(5+6-3\right)\)
\(=x^2-2x+8\)
Hệ số tự do của đa thức F(x) là: 8
Hệ số bậc 1 của đa thức F(x) là: -2
b) \(F\left(x\right)=x^2-2x+8\); \(G\left(x\right)=-x^2-2x-9\)
+) \(\Rightarrow F\left(x\right)+G\left(x\right)=\left(x^2-2x+8\right)+\left(-x^2-2x-9\right)\)
\(=\left(x^2-x^2\right)+\left(-2x-2x\right)+\left(8-9\right)=-4x-1\)
Vậy \(M\left(x\right)=-4x-1\)
+) và \(F\left(x\right)-G\left(x\right)=\left(x^2-2x+8\right)-\left(-x^2-2x-9\right)\)
\(=\left(x^2+x^2\right)+\left(-2x+2x\right)+\left(8+9\right)=2x^2+17\)
Vậy \(N\left(x\right)=2x^2+17\)
c)
+) M(x) có nghiệm khị và chỉ khi M(x) = 0
\(\Leftrightarrow-4x-1=0\Leftrightarrow-4x=1\Leftrightarrow x=\frac{-1}{4}\)
Vậy M(x) có 1 nghiệm là \(\frac{-1}{4}\)
+) N(x) có nghiệm khị và chỉ khi N(x) = 0
\(\Leftrightarrow2x^2+17=0\)
Mà \(2x^2+17\ge17\left(dox^2\ge0\right)\)
Nên N(x) vô nghiệm
d) F(x) = x2 - 3\(\Leftrightarrow x^2-2x+8=x^2-3\Leftrightarrow-2x=-11\)
\(\Leftrightarrow x=\frac{11}{2}\)
Vậy \(x=\frac{11}{2}\)thì F(x) = x2 - 3
Thu gọn và sắp xếp các hạng tử theo luỹ thừa giảm dần của biến. Tìm bậc, hệ số tự do, hệ số cao nhất của đa thức.
a) A(x) = \(x^7-2x^6+2x^3-2x^4-x^7+x^5+2x^6-x+5+2x^4-x^5\)
b) B(x) = \(-3x^5+4x^4-2x+\dfrac{1}{2}-2x^4+3x-x^5-2x^4+\dfrac{5}{2}+x\)
c) C(y) = \(5y^2-2\left(y+1\right)+3y\left(y^2-2\right)+5\)
a) \(A\left(x\right)=x^7-2x^6+2x^3-2x^4-x^7+x^5+2x^6-x+5+2x^4-x^5\)
\(A\left(x\right)=(x^7-x^7)+(-2x^6+2x^6)+2x^3+(-2x^4+2x^4)+(x^5-x^5)-x+5\)
\(A\left(x\right)=2x^3-x+5\)
- Bậc của đa thức A(x) là 3
- Hệ số tự do: 5
- Hệ số cao nhất: 2
b) \(B\left(x\right)=-3x^5+4x^4-2x+\dfrac{1}{2}-2x^4+3x-x^5-2x^4+\dfrac{5}{2}+x\)
\(B\left(x\right)=(-3x^5-x^5)+(4x^4-2x^4-2x^4)+(-2x+x+3x)+\left(\dfrac{1}{2}+\dfrac{5}{2}\right)\)
\(B\left(x\right)=-4x^5+2x+3\)
- Bậc của đa thức B(x) là 5
- Hệ số tự do: 3
- Hệ số cao nhất: \(-4\)
c) \(C\left(y\right)=5y^2-2.\left(y+1\right)+3y.\left(y^2-2\right)+5\)
\(C\left(y\right)=5y^2-2y-2+3y\left(y^2-2\right)+5\)
\(C\left(y\right)=5y^2-2y-2+3y^3-6y+5\)
\(C\left(y\right)=5y^2-2y+3+3y^3-6y\)
\(C\left(y\right)=5y^2-8y+3+3y^3\)
\(C\left(y\right)=3y^3+5y^2-8y+3\)
- Bậc của đa thức C(y) là 3
- Hệ số tự do: 3
- Hệ số cao nhất: 3
Đúng 2
Bình luận (0)
Cho đa thức M(x) = -3 + 2x^7 + ax^8 - 1/3x^7 + 5/6x^8 + b. Tìm a và b biết đa thức có hệ số cao nhất là 5, hệ số tự do là 4.
________Các bạn giúp mình nha. Mai mình phải nộp cho cô rùi! Thank you! ^-^-^-^-^-^^-^-^_________
ta có: \(M_{\left(x\right)}=-3+2x^7+ax^8-\frac{1}{3}x^7+\frac{5}{6}x^8+b\)
\(M_{\left(x\right)}=-3+\left(2x^7-\frac{1}{3}x^7\right)+\left(ax^8+\frac{5}{6}x^8\right)+b\)
\(M_{\left(x\right)}=-3+\frac{5}{3}x^7+\left(a+\frac{5}{6}\right)x^8+b\)
mà hệ số cao nhất của đa thức là:5
=> ( a + 5/6 ) x^8 có hệ số là 5 ( vì đa thức có bậc cao nhất và không có hạng tử nào trong đa thức có bậc là 5)
=> a+ 5/6 = 5
a = 5 - 5/6
a= 25/6
mà hệ số tự do của đa thức là 4
mà -3 có hệ số tự do là : -3 ( hay hệ số của nó = -3)
=> b= 4 ( vì trong đa thức không có hạng tử nào có hệ số tự do là 4)
KL: a= 25/6 ; b=4
CHÚC BN HỌC TỐT!!!!!
Đúng 0
Bình luận (0)
3.15 giải các phương trình sau :
a) ( x - 6 ) ( 2x - 5 ) ( 3x + 9 ) = 0
b) 2x( x - 3 ) + 5( x - 3 ) = 0
c) ( x^2 - 4 ) - ( x - 2 ) ( 3 - 2x ) =0
3.16 tìm m để phương trình sau có nghiệm :
x=-7 ( 2m - 5 )x - 2m^2 + 8
3.17 giải các phương trình sau :
a) ( 2x - 1 )^2 - ( 2x + 1 ) = 0
\(a,\left(x-6\right)\left(2x-5\right)\left(3x+9\right)=0\Leftrightarrow\left[{}\begin{matrix}x-6=0\Leftrightarrow x=6\\2x-5=0\Leftrightarrow x=\dfrac{5}{2}\\3x+9=0\Leftrightarrow x=-3\end{matrix}\right.\)
\(b,2x\left(x-3\right)+5\left(x-3\right)=0\Leftrightarrow\left(2x+5\right)\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x-3=0\Leftrightarrow x=3\\2x+5=0\Leftrightarrow x=-\dfrac{5}{2}\end{matrix}\right.\)
\(c,x^2-4-\left(x-2\right)\left(3-2x\right)=0\Leftrightarrow\left(x-2\right)\left(x+2\right)-\left(x-2\right)\left(3-2x\right)=0\Leftrightarrow\left(x-2\right)\left(x+2-3+2x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)
\(x=-7\left(2m-5\right)x-2m^2+8\Leftrightarrow x+7\left(2m-5\right)=8-2m^2\Leftrightarrow x\left(14m-34\right)=8-2m^2\)
\(ycđb\Leftrightarrow14m-34\ne0\Leftrightarrow m\ne\dfrac{34}{14}\)\(\Rightarrow x=\dfrac{8-2m^2}{14m-34}\)
\(3.17\Leftrightarrow4x^2-4x+1-2x-1=0\Leftrightarrow4x^2-6x=0\Leftrightarrow x\left(4x-6\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
3.15:
a, \(\Leftrightarrow\left\{{}\begin{matrix}x-6=0\\2x-5=0\\3x+9=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\x=\dfrac{5}{2}\\x=-\dfrac{9}{3}=-3\end{matrix}\right.\)
b, \(\Leftrightarrow\left(x-3\right)\left(2x+5\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\2x+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\x=-\dfrac{5}{2}\end{matrix}\right.\)
c, \(\Leftrightarrow\left(x-2\right)\left(x+2\right)-\left(x-2\right)\left(3-2x\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2-3+2x\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2=0\\3x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)
3.16
\(\Leftrightarrow\left(2m-5\right).-7-2m^2+8=0\)
\(\Leftrightarrow-14m+35-2m^2+8=0\)
\(\Leftrightarrow-14m-2m^2+43=0\)
\(\Leftrightarrow-2\left(7m+m^2\right)=-43\)
\(\Leftrightarrow m\left(7-m\right)=\dfrac{43}{2}\)
\(\Leftrightarrow\dfrac{m\left(7-m\right)}{1}-\dfrac{43}{2}=0\)
\(\Leftrightarrow\dfrac{14m-2m^2}{2}-\dfrac{43}{2}=0\)
pt vô nghiệm
Đúng 1
Bình luận (0)
Tìm m để các hàm số sau là hàm số bậc nhất:
a. y = (2m - 1)x + 3
b. y = \(\dfrac{m-2}{2m+1}x+5\)
c. y = \(\sqrt{m-2}.x-4\)
d. y = (m2 - 9)x2 + (m - 3)x + 5
Cho đa thức P = x^4 – 3 (x-1) + x^3 – 2x + x^2 – 1 – 2x^4
Q = -3x^2 + 2x (x+3) + 3x^4 – x(3x^2 +5 ) – 2
a) Thu gọn các đa thức trên rồi xác định hệ số cao nhất , hệ số tự do và tìm bậc của mỗi đa thức
Tìm đa thức M biết M = 3P +Q
a, \(P=-x^4+x^3+x^2-5x+2\)
hế số cao nhất 2 ; hế số tự do 2 ; bậc 4
\(Q=-3x^2+2x^2+6x+3x^4-3x^3-5x-2=3x^4-3x^3-x^2+x-2\)
hệ số cao nhất 3 ; hệ số tự do -2 ; bậc 4
b, \(M=-3x^4+3x^3+3x^2-15x+6+3x^4-3x^3-x^2+x-2=2x^2-14x+4\)
Đúng 0
Bình luận (0)