a)Xét tứ giác MBOC có 

\(\widehat{OBM}\) và \(\widehat{OCM}\) là hai góc đối

\(\widehat{OBM}+\widehat{OCM}=180^0\left(90^0+90^0=180^0\right)\)

Do đó: MBOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

Đáp án C

Tam giác ABC có góc A là góc tù nên 

Mà cạnh đối diện với góc A là cạnh BC .

Áp dụng định lí: trong 1 tam giác cạnh đối diện với góc lớn hơn thì lớn hơn ta được:

BC > AC và BC > AB

Vậy tam giác ABC có độ dài cạnh BC là lớn nhất nên dây BC gần tâm nhất.

Chưa thể kết luận dây nào xa tâm nhất.

a: góc BHD+góc BMD=180 độ

=>BHDM nội tiếp

b: BHDM nội tiếp

=>góc HDM+góc HBM=180 độ

=>góc ADM=góc ABC

=>góc ADM=góc ADC

=>DA là phân giáccủa góc MDC

c: Xét tứ giác DHNC có

góc DHC=góc DNC=90 độ

=>DHNC nội tiếp

=>góc NHD=góc NDC

góc NHD+góc MHD

=180 độ-góc NCD+góc MBD

=180  độ+180 độ-góc ABD-góc ACD

=180 độ

=>M,H,N thẳng hàng

\(\cos A=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{8^2+10^2-13^2}{2\cdot8\cdot10}=-\dfrac{1}{32}< 0\)

nên \(\widehat{A}>90^0\)

=>ΔABC tù

1)Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC, K là giao điểm thứ hai của AH với đường tròn (O). Đường thẳng đi qua H và vuông góc với OA cắt BC ở I. Chứng minh rằng IK là tiếp tuyến của đường tròn (O)

 ~~~~~~~~~ Bài làm ~~~~~~~~~

Ta có: \(\widehat{HBD}=\widehat{DAC}\) (Cùng phụ với \(\widehat{ACB}\))

\(\widehat{KBD}=\widehat{DAC}\)( Góc nối tiếp cùng chắn cung \(KC\))

\(\Rightarrow\widehat{HBD}=\widehat{KBD}\)

Ta lại có: \(BD\perp HK\)

\(\Rightarrow BD\) là đường trung trực của \(HK\)

\(\Rightarrow\Delta IHK\) cân tại \(I\)

\(\Rightarrow\widehat{BKD}=\widehat{BHD}=\widehat{AHQ}\)

Lại có:\(\widehat{DKO}=\widehat{HAO}\)( \(\Delta OKA\) cân tại \(O\))

Vì vậy: \(\widehat{DKO}+\widehat{BKD}=\widehat{HAO}+\widehat{AHQ}=90^0\)

\(\Rightarrow\widehat{KIO}=90^0\)

\(\Rightarrow IK\)là tiếp tuyến của đường tròn \(\left(O\right)\)

(Hình vẽ chỉ mang tính chất minh họa cái hình vẽ gần cả tiếng đồng hồ :)) )

Ủa bạn ơi sao phụ nhau? Dòng đầu ấy

Đúng rồi bạn. Phụ nhau ý nghĩa là ^HBD + ^ACB = 90^0 và tương tự như góc kia. (Tam giác vuông ý)

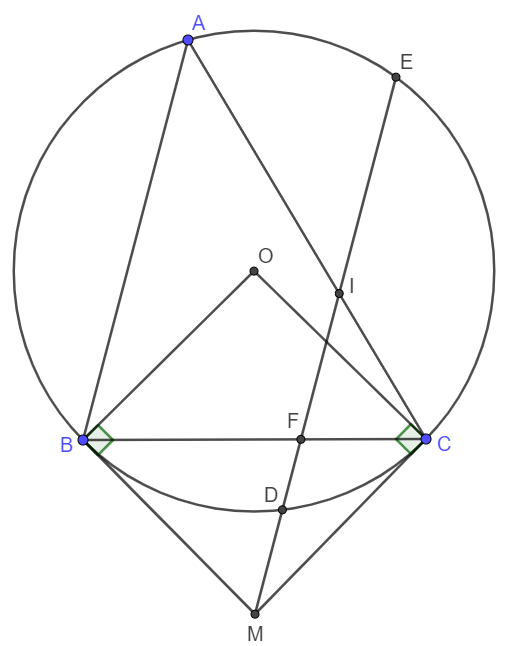
Cho tam giác $ABC$ không có góc tù $(AB<AC)$, nội tiếp đường tròn $(O;R)$, ($B$, $C$ cố định, $A$ di động trên cung lớn BC). Các tiếp tuyến tại $B$ và $C$ cắt nhau tại $M$. Từ $M$ kẻ đường thẳng song song với $AB$, đường thẳng này cắt $(O)$ tại $D$ và $E$ ($D$ thuộc cung nhỏ $BC$), cắt $BC$ tại $F$, cắt $AC$ tại $I$. Chứng minh rằng \widehat{MBC}=\widehat{BAC}MBC=BAC . Từ đó suy ra $MBIC$ là tứ giác nội tiếp.

 theo gt, ta co:

goc MBC= BAC (cung chan cung BC)

mat khac, ta lai co goc BAC = MIC ( dong vi)

=> goc MBC= MIC

=> tu giac BICM noi tiep 

opps hihi xin lỗi lúc nảy em làm vội nên sai,thế này mới chính là câu trả lời của em

Lời giải. Kẻ OA₁⊥BC,OB₁⊥AC,OC₁⊥AB. Khi đó tứ giác OA₁C₁B,OA₁B₁C,OC₁AB₁ nội tiếp nên theo định lý Ploteme ta có

     ⎨aR=bz+cy

        az=cx+bR⇒R(a+b+c)=b(z−x)+c(y−x)+a(y+z)(1)

        ay=bx+cR

Ta lại có 2SABC=r(a+b+c)=cz+by−ax (2)

Cộng (1)với (2) ta thu được R+r=y+z−x. ■