cho tam giác abc vuông tại a có đường cao ch. cm:ac+ab<ab+ch
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A (ABAC).Trên cạnh BC lấy điểm D sao cho BDAB.Qua D kẻ đường thẳng d vuông góc với BC a) CM:ACBE b) Gọi K là giao điểm của DE và AC : CM: Tam giác KCE cân c) CM: BK là tia phân giác của góc BAC
Đọc tiếp
Cho tam giác ABC vuông tại A (AB<AC).Trên cạnh BC lấy điểm D sao cho BD=AB.Qua D kẻ đường thẳng d vuông góc với BC a) CM:AC=BE b) Gọi K là giao điểm của DE và AC : CM: Tam giác KCE cân c) CM: BK là tia phân giác của góc BAC
Cho tam giác ABC vuông tại A, đường cao AH,trung tuyến AM,Q ua H kẻ đt song song với AB cắt AC tại D.Qua H kẻ đt song song với AC cắt AB tại E.CM:
a)AH=DE
b)AM vuông góc với DE
c)Cho AB=6. CM:AC=8 và tính diện tích AEMD
d)tam giác ABC thêm đk gì để AEHD là hình vuông
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH = 5cm. Biết CH = 6cm. tính:
a) AB, AC,BC và BH?
b) Diện tích tam giác ABC
Bài2: Cho tam giác ABC vuông tại A, đường cao AH; AB = 15cm; BC = 25cm. BTính:
a) AC,AH, HC và BH?
b) Diện tích tam giác ABC
\(1,\)
\(a,\) Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AH^2=CH\cdot BH\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AH^2}{CH}=\dfrac{25}{6}\left(cm\right)\\AB=\sqrt{\dfrac{25}{6}\left(\dfrac{25}{6}+6\right)}=\dfrac{5\sqrt{61}}{6}\left(cm\right)\\AC=\sqrt{6\left(\dfrac{25}{6}+6\right)}=\sqrt{61}\left(cm\right)\end{matrix}\right.\\ BC=\dfrac{25}{6}+6=\dfrac{61}{6}\left(cm\right)\)
\(b,S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot5\cdot\dfrac{61}{6}=\dfrac{305}{12}\left(cm^2\right)\)
Đúng 3
Bình luận (0)
Cho tam giac ABC vuông tại C có góc A=60độ.Tia phân giác góc BAC cắt BC ở E . Kẻ EK vuông góc với AB ở .Kẻ Bd vuông góc với AE ở E.
a,CM:AC=AK và CK vuông góc AE
b,CM:AB=2AC
c,CM:EB>AC
d,CM:AC,EK và BD là 3 đường dồng quy
1. Cho tam giác ABC vuông tại A(AB<AC) có đường cao AH. Biết BC = 25cm, AH = 12cm. Tính AB, AC, BH, CH
2. Cho tam giác ABC vuồng tại A, đường cao AH. Biết AB = 15cm, HC = 16cm. Tính AC, BC, AH, BH
1.Cho tam giác ABC vuông tại A. Gọi H là chân đường cao hạ từ A. Biết rằng AB = 7cm, AC = 9cm. Tính BH, CH, AH.
2. Cho tam giác ABC vuông tại A, đường cao AH. BH = 4cm, CH=9cm. Tính AH,AB,AC?
BÀI 2 : áp dụng hệ thức lượng trong tam giác, ta có: AH^2=BH*CH=>AH^2= 4*9=36=>AH=căn bậc hai của 36=6
\(AB^2=BH\cdot BC=4\cdot\left(4+9\right)=52=>AB=\sqrt{52}=2\sqrt{13}\)
\(AC^2=CH\cdot BC=9\cdot13=117=>AC=\sqrt{117}=3\sqrt{13}\)
Đúng 0
Bình luận (0)
1, Cho tam giác ABC vuông tại A,đường cao AH
a, Cho biêt AB=3cm,BC=5cm.Tính độ dài đoạn thẳng BH,CH,AH và AC
b,Cho biết AH=60cm,CH=144cm.Tính độ dài đoạn thẳng AB,AC,BC và BH
2, Cho tam giác ABC vuông tại A, đường cao AH
Cho biết \(\dfrac{AB}{AC}\)=\(\dfrac{5}{6}\) và BC=122cm.Tính độ dài các đoạn thẳng BH,CH
Bài 2:
Ta có: \(\dfrac{AB}{AC}=\dfrac{5}{6}\)
\(\Leftrightarrow\dfrac{HB}{HC}=\dfrac{25}{36}\)
\(\Leftrightarrow HB=\dfrac{25}{36}HC\)
Ta có: HB+HC=BC
\(\Leftrightarrow HC\cdot\dfrac{61}{36}=122\)
\(\Leftrightarrow HC=72\left(cm\right)\)
hay HB=50(cm)
Đúng 1
Bình luận (0)
1) a. cho tam giác ABC vuong tại A . AB = 7 , AC =9 . Đường cao AH . TÍNH BC và AH
b. cho tam giác ABC vuông tại A .AB = AC. Đường cao AH . BH = CH. AH =5 . Tính AB ,AC ,BH ,CH
VẼ HÌNH HƠI XẤU THÔNG CẢM NHA
áp dụng hệ thức lượng trong tam giác vuông ABC ta có \(AB\cdot AC=AH\cdot BC\) \(\Rightarrow AH\cdot BC=63\) (1)
áp dụng đl pitagovao tam giác vuông ABC ta có \(AB^2+AC^2=BC^2\Rightarrow BC=\sqrt{130}\)
thay vao (1) ta co \(AH\cdot BC=63\Rightarrow AH=\frac{63}{\sqrt{130}}\)
Đúng 1
Bình luận (0)
cho tam giác abc vuông tại a có đường cao ah.biết ab = 19.5 . ah =18cm ch=5.76 nhan bh.tính chu vi tam giác
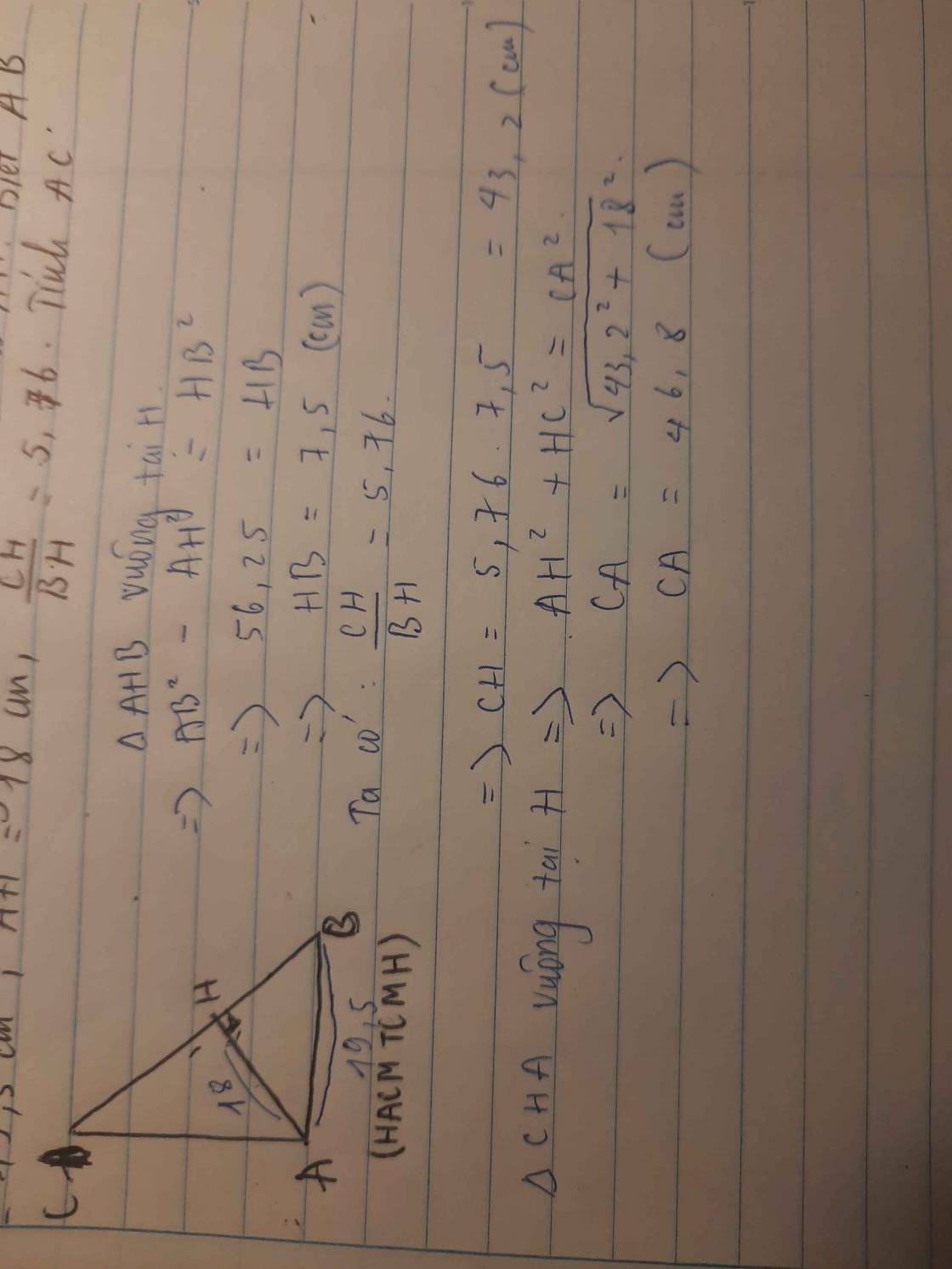BC=BH+CH
=7,5+43,2
=50,7
CVabc= 50.7+19.5+46.8
Đúng 0
Bình luận (0)