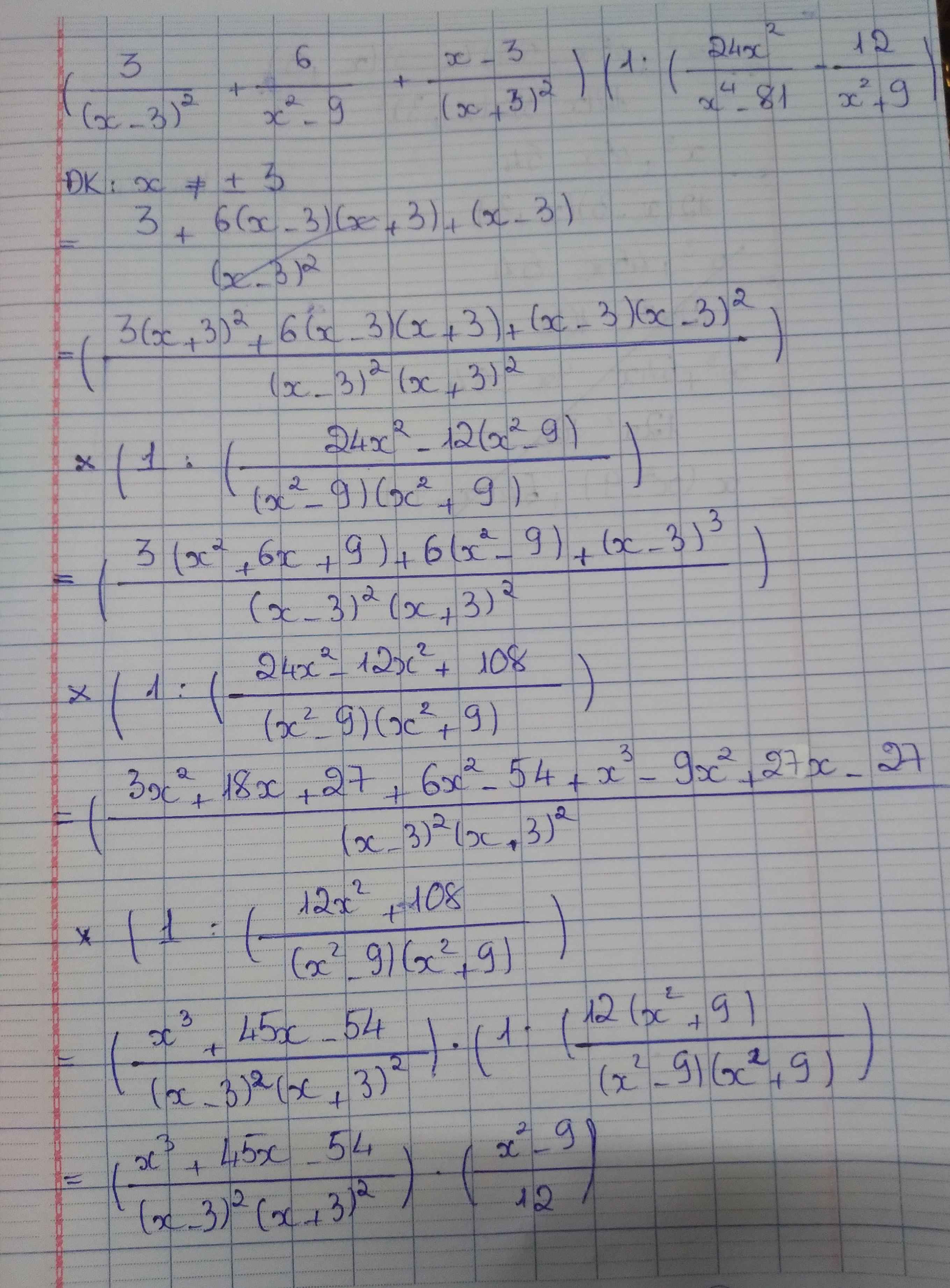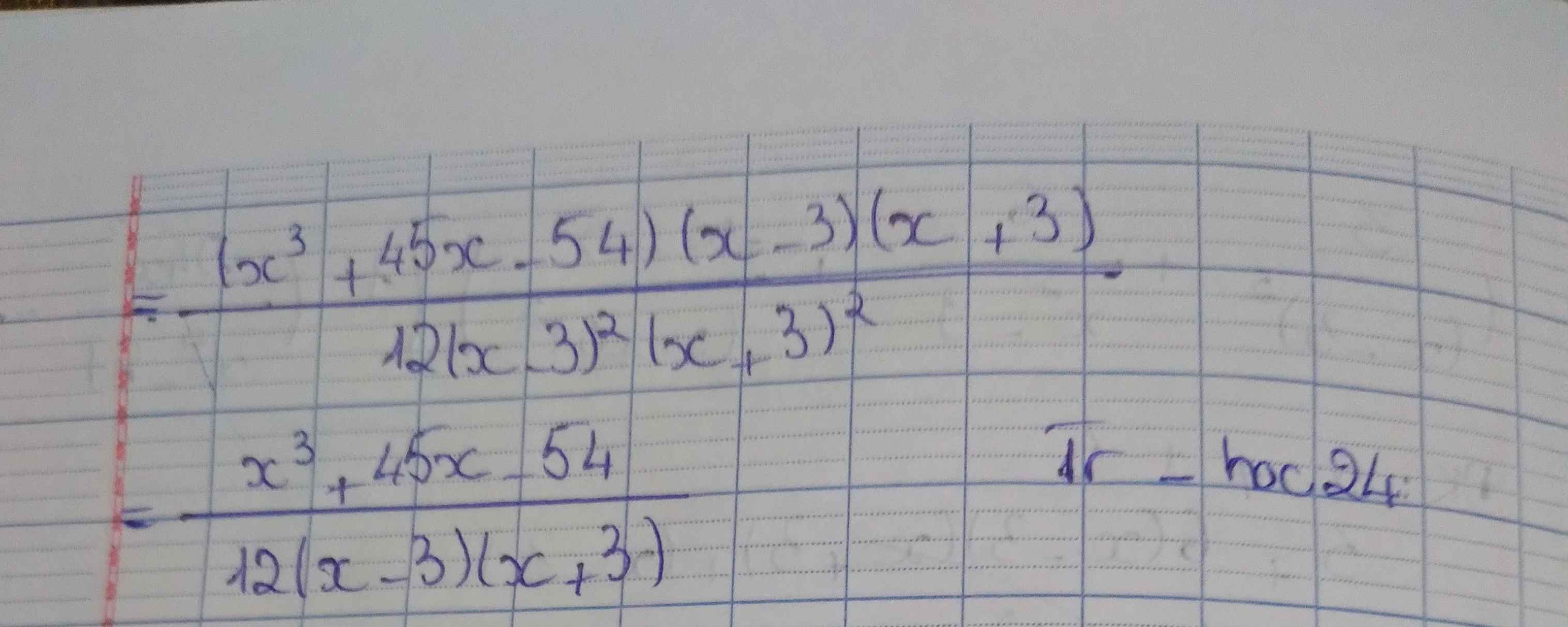\(\left(x+4\right)\left(x+6\right)\left(x-2\right)\left(x-12\right)=25x^2\)

\(\Leftrightarrow\left(x+3\right)\left(x+8\right)\left(x^2-15x+24\right)=0\)

\(x^4-8x^3+21x^2-24x+9=0\)

\(\Leftrightarrow\left(x^2-3x+3\right)\left(x^2-5x+3\right)=0\)

\(\Leftrightarrow\left(x-\frac{5+\sqrt{13}}{2}\right)\left(x-\frac{5-\sqrt{13}}{2}\right)=0\) (vì \(x^2-3x+3=\left(x-\frac{3}{2}\right)^2+0,75>0\))

\(\Rightarrow\orbr{\begin{cases}x=\frac{5+\sqrt{13}}{2}\\x=\frac{5-\sqrt{13}}{2}\end{cases}}\)

\(\left(x-3\right)\left(x-5\right)\left(x-6\right)\left(x-10\right)=24x^2\)

\(\Leftrightarrow x^4-24x^3+203x^2-720x+900=24x^4\)

\(\Leftrightarrow x^4-24x^3+203x^2-720x+900-24x^2=0\)

\(\Leftrightarrow x^4-24x^3+179x^3-720x+900=0\)

\(\Leftrightarrow\left(x-2\right)\left(x-15\right)\left(x^2-7x+30\right)=0\)

có: \(x^2-7x+30\ne0\), nên:

\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x-15=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=2\\x=15\end{cases}}\)

\(\left(x-3\right)\left(x-5\right)\left(x-6\right)\left(x-10\right)=24x^2\)

\(\Leftrightarrow\left[\left(x-5\right)\left(x-6\right)\right]\cdot\left[\left(x-3\right)\left(x-10\right)\right]=24x^2\)

\(\Leftrightarrow\left(x^2-11x+30\right)\left(x^2-13x+30\right)-24x^2=0\)

Đặt: \(x^2-13x+30=t\)

Lúc này PT trở thành:

\(t\left(t+2x\right)-24x^2=0\)

\(\Leftrightarrow t^2+2tx-24x^2=0\)

\(\Leftrightarrow t^2+6tx-4tx-24x^2=0\)

\(\Leftrightarrow t\left(t+6x\right)-4x\left(t+6x\right)=0\)

\(\Leftrightarrow\left(t+6x\right)\left(t-4x\right)=0\)

\(\Leftrightarrow\left(x^2-7x+30\right)\left(x^2-17x+30\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2-7x+30=0\\x^2-17x+30=0\end{matrix}\right.\)

Ta có: \(x^2-7x+30=\left(x-\dfrac{7}{2}\right)^2+\dfrac{71}{4}>0\)(vô nghiệm)

=> \(x^2-17x+30=0\)

\(\Leftrightarrow\) \(\left(x-15\right)\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-15=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=15\\x=2\end{matrix}\right.\)

Vậy x = 2 hoặc x = 15

\(\left(x-3\right)\left(x-5\right)\left(x-6\right)\left(x-10\right)=24x^2\) (1)

\(\Leftrightarrow\left(x^2-5x-3x+15\right)\left(x-6\right)\left(x-10\right)=24x^2\)

\(\Leftrightarrow\left(x^2-8x+15\right)\left(x-6\right)\left(x-10\right)=24x^2\)

\(\Leftrightarrow\left(x^3-6x^2-8x^2+48x+15x-90\right)\left(x-10\right)=24x^2\)

\(\Leftrightarrow\left(x^3-14x^2+63x-90\right)\left(x-10\right)=24x^2\)

\(\Leftrightarrow x^4-10x^3-14x^3+140x^2+63x^2-630x-90x+900=24x^2\)

\(\Leftrightarrow x^4-2x^3-22x^3+44x^2+135x^2-270x-450x+900=0\)

\(\Leftrightarrow x^3\left(x-2\right)-22x^2\left(x-2\right)+135x\left(x-2\right)-450\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x^3-22x^2+135x-450\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x^3-15x^2-7x^2+105x+30x-450\right)=0\)

\(\Leftrightarrow\left(x-2\right)\cdot\left[x^2\cdot\left(x-15\right)-7x\left(x-15\right)+30\left(x-15\right)\right]=0\)

\(\Leftrightarrow\left(x-2\right)\left(x-15\right)\left(x^2-7x+30\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x-15=0\\x^2-7x+30=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=15\\x\notin R\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=15\end{matrix}\right.\)

Vậy tập nghiệm phương trình (1) là \(S=\left\{2;15\right\}\)

PT\(\Leftrightarrow\)\(\left[\left(x-3\right)\left(x-10\right)\right]\left[\left(x-5\right)\left(x-6\right)\right]=24x^2\)

\(\Leftrightarrow\)\(\left(x^2-13x+30\right)\left(x^2-11x+30\right)=24x^2\)

Nhận thấy x=0 không là nghiệm của PT. Chia cả hai vế của phương trình cho \(x^2\) ta được:

PT\(\Leftrightarrow\)\(\left(x-13+\dfrac{30}{x}\right)\left(x-11+\dfrac{30}{x}\right)=24\)

Đặt \(x+\dfrac{30}{x}=t\) (1)

PT\(\Leftrightarrow\)\(\left(t-13\right)\left(t-11\right)=24\)

Tìm được \(\left[{}\begin{matrix}t=17\\t=7\end{matrix}\right.\)

Thay vào (1):\(\left[{}\begin{matrix}x^2-17x+30=0\\x^2-7x+30=0\end{matrix}\right.\)

Tìm được \(\left[{}\begin{matrix}x=15\\x=2\end{matrix}\right.\)

Bạn ơi mik ra \(\dfrac{x^3+45x-54}{12\left(x-3\right)\left(x+3\right)}\) có đúng không bạn?

Lần sau đừng tự tiện xếp vào phần bất pt bạn nhé :(

Ta có : \(4\left(x+5\right)\left(x+6\right)\left(x+10\right)\left(x+12\right)=3x^2\)

\(\Leftrightarrow4\left(x+5\right)\left(x+12\right)\left(x+6\right)\left(x+10\right)=3x^2\)

\(\Leftrightarrow4\left(x^2+17x+60\right)\left(x^2+16x+60\right)=3x^2\)(1)

Đặt \(x^2+16x+60=a\)

Pt (1) \(\Leftrightarrow4\left(a+x\right)a=3x^2\)

         \(\Leftrightarrow4\left(a^2+ax\right)=3x^2\)

          \(\Leftrightarrow4a^2+4ax=3x^2\)

          \(\Leftrightarrow4a^2+4ax+x^2=4x^2\)

         \(\Leftrightarrow\left(2a+x\right)^2=4x^2\)

          \(\Leftrightarrow\orbr{\begin{cases}2a+x=2x\\2a+x=-2x\end{cases}}\)

*Nếu \(2a+x=2x\)

\(\Leftrightarrow2a=x\)

\(\Leftrightarrow x^2+16x+60=x\)

\(\Leftrightarrow x^2+15x+60=0\)

\(\Leftrightarrow x^2+2.\frac{15}{2}.x+\frac{225}{4}+\frac{15}{4}=0\)

\(\Leftrightarrow\left(x+\frac{15}{2}\right)^2+\frac{15}{4}=0\)

Pt vô nghiệm

*Nếu \(2a+x=-2x\)

\(\Leftrightarrow2a+3x=0\)

\(\Leftrightarrow2\left(x^2-16x+60\right)+3x=0\)

\(\Leftrightarrow2x^2-32x+120+3x=0\)

\(\Leftrightarrow2x^2-29x+120=0\)

\(\Leftrightarrow x^2-\frac{29}{2}x+60=0\)

\(\Leftrightarrow x^2-2.\frac{29}{4}.x+\frac{841}{16}+\frac{119}{16}=0\)

\(\Leftrightarrow\left(x-\frac{29}{4}\right)^2+\frac{119}{16}=0\)

Pt vô nghiệm

Vậy pt vô nghiệm

a)

\((x-3)(x-5)(x-6)(x-10)=24x^2\)

\(\Leftrightarrow [(x-3)(x-10)][(x-5)(x-6)]=24x^2\)

\(\Leftrightarrow (x^2-13x+30)(x^2-11x+30)=24x^2\)

Đặt \(x^2-11x+30=a\). PT trở thành:
\((a-2x)a=24x^2\)

\(\Leftrightarrow a^2-2ax-24x^2=0\)

\(\Leftrightarrow a^2-6ax+4ax-24x^2=0\)

\(\Leftrightarrow a(a-6x)+4x(a-6x)=0\)

\(\Leftrightarrow (a+4x)(a-6x)=0\)

\(\Rightarrow \left[\begin{matrix} a+4x=0\\ a-6x=0\end{matrix}\right.\Rightarrow \left[\begin{matrix} x^2-7x+30=0\\ x^2-17x+30=0\end{matrix}\right.\)

\(\Rightarrow \left[\begin{matrix} (x-3,5)^2+17,75=0(\text{vô lý})\\ (x-15)(x-2)=0\end{matrix}\right.\)

\(\Rightarrow x=15\) hoặc $x=2$

b)

Đặt \(x-7=a\). PT trở thành:

\((a+1)^4+(a-1)^4=272\)

\(\Leftrightarrow a^4+4a^3+6a^2+4a+1+a^4-4a^3+6a^2-4a+1=272\)

\(\Leftrightarrow 2a^4+12a^2+2=272\)

\(\Leftrightarrow a^4+6a^2-135=0\)

\(\Leftrightarrow (a^2+3)^2-144=0\Leftrightarrow (a^2+3)^2-12^2=0\)

\(\Leftrightarrow (a^2+15)(a^2-9)=0\)

\(\Rightarrow a^2-9=0\Rightarrow a=\pm 3\)

\(\Rightarrow x=a+7=\left[\begin{matrix} 4\\ 10\end{matrix}\right.\)

c)

\(x^4-3x^3+2x^2-9x+9=0\)

Ta để ý tổng các hệ số bằng $0$ nên có một nghiệm bằng $1$

Vậy ta thực hiện tách hợp lý:

\(\Leftrightarrow (x^4-x^3)-(2x^3-2x^2)-(9x-9)=0\)

\(\Leftrightarrow x^3(x-1)-2x^2(x-1)-9(x-1)=0\)

\(\Leftrightarrow (x-1)(x^3-2x^2-9)=0\)

\(\Leftrightarrow (x-1)[(x^3-3x^2)+x^2-9]=0\)

\(\Leftrightarrow (x-1)[x^2(x-3)+(x-3)(x+3)]=0\)

\(\Leftrightarrow (x-1)(x-3)(x^2+x+3)=0\)

Dễ thấy \(x^2+x+3=(x+\frac{1}{2})^2+\frac{11}{4}\geq 0+\frac{11}{4}>0\) với mọi $x$

Do đó: \((x-1)(x-3)=0\Rightarrow \left[\begin{matrix} x=1\\ x=3\end{matrix}\right.\)