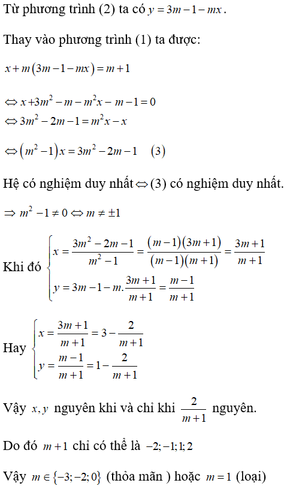x² - 25 = y(y + 6)

<=> x² - 25 = y² + 6y

<=> x² - 25 - y² - 6y = 0

<=> \(\left\{{}\begin{matrix}x=\sqrt{6y+y^2+25}\\y=\sqrt{x^2-25-6y}\end{matrix}\right.\)

\(x^2-25=y\left(y+6\right)\Leftrightarrow x^2-16=y^2+6y+9\Leftrightarrow x^2-\left(y+3\right)^2=16\)

\(\Leftrightarrow\left(x-y-3\right)\left(x+y+3\right)=16\)

Tới đây bạn tự làm nhé :)

sorry mk mới lớp 6 nên ko biết

Từ PT (1) ta có: y = (a + 1)x – (a + 1) (*) thế vào PT (2) ta được:

x + ( a – 1 ) [ ( a + 1 ) x – ( a + 1 ) ] = 2   x + ( a 2 – 1 ) x – ( a 2 – 1 ) = 2

⇔ a 2 x = a 2 + 1   ( 3 )

Với a ≠ 0, phương trình (3) có nghiệm duy nhất x = a 2 + 1 a 2 . Thay vào (*) ta có:

y = ( a + 1 ) a 2 + 1 a 2 − ( a + 1 ) = a + 1 a 2 + 1 − a 2 a 2 + 1 a 2 = a 3 + a + a 2 + 1 − a 3 − a 2 a 2 = a + 1 a 2  

Suy ra hệ phương trình đã cho có nghiệm duy nhất ( x ;   y ) = a 2 + 1 a 2 ; a + 1 a 2

Hệ phương trình có nghiệm nguyên: x ∈ ℤ y ∈ ℤ ⇔ a 2 + 1 a 2 ∈ ℤ a + 1 a 2 ∈ ℤ ( a ∈ ℤ )  

Điều kiện cần: x = a 2 + 1 a 2 = 1 + 1 a 2 ∈ ℤ ⇔ 1 a 2 ∈ ℤ mà a 2 > 0   ⇒ a 2 = 1

⇔ a = ± 1 ( T M   a ≠ 0 )

Điều kiện đủ:

a = −1 ⇒  y = 0  (nhận)

a = 1 ⇒  y = 2  (nhận) 

Vậy a = ± 1 hệ phương trình đã cho có nghiệm nguyên.

Đáp án: D

Câu trả lời hay nhất:  Giai cau a) 
x³ - y³ = xy + 8 
<=> (x - y)³ + 3xy(x - y) - xy = 8 
<=> (x - y)³ + xy(3x - 3y - 1) = 8 
<=> (3x - 3y)³ + 27xy(3x - 3y - 1) = 216 
<=> (3x - 3y)³ - 1 + 27xy(3x - 3y - 1) = 215 
<=> (3x - 3y - 1)[(3x - 3y)² + (3x - 3y) + 1] + 27xy(3x - 3y - 1) = 215 
<=> (3x - 3y - 1)[(3x - 3y)² + (3x - 3y) + 1 + 27xy] = 215 
<=> (3x - 3y - 1)(9x² + 9y² - 9xy + 3x - 3y + 1) = 215 = 5.43 = 43.5 = (- 5)(- 43) = (- 43)(- 5) 

{ 3x - 3y - 1 = 5 (1) 
{ 9x² + 9y² - 9xy + 3x - 3y + 1 = 43 (2) 
Tu (1) => y = x - 2 thay vao (2) khai trien rut gon co x(x - 2) = 0 
=> x = 0; x = 2 => y = - 2; y = 0 
Truong hop nay he co 2 nghiem nguyen (x;y) = (0; - 2) va (2; 0) 

{ 3x - 3y - 1 = 43 (3) 
{ 9x² + 9y² - 9xy + 3x - 3y + 1 = 5 (4) 

{ 3x - 3y - 1 = - 5 (5) 
{ 9x² + 9y² - 9xy + 3x - 3y + 1 = - 43 (6) 

{ 3x - 3y - 1 = - 43 (7) 
{ 9x² + 9y² - 9xy + 3x - 3y + 1 = - 5 (8) 
Ban tu giai tiep 3 he sau ( chu y chon nghiem nguyen ) roi ket luan 
-------------------------------------… 
Ban xem vi du sau: Giai pt nghiem nguyen 
2x² - 2x - 2y² = - 3 
<=> 4x² - 4x - 4y² + 1 = - 5 
<=> (2x + 2y - 1)(2x - 2y - 1) = - 5 = - 1.5 = 1.(- 5) = 5.( -1 ) = (- 5).1 

{ 2x + 2y - 1 = - 1 
{ 2x - 2y - 1 = 5 
=> x = 3/2 ; y = - 3/2 ( loai ) 

{ 2x + 2y - 1 = 1 
{ 2x - 2y - 1 = - 5 
=> x = - 1/2 ; y = 3/2 ( loai ) 

{ 2x + 2y - 1 = 5 
{ 2x - 2y - 1 = - 1 
=> x = 3/2 ; y = 3/2 ( loai ) 

{ 2x + 2y - 1 = - 5 
{ 2x - 2y - 1 = 1 
=> x = - 1/2 ; y = - 3/2 ( loai) 
KL : Pt khong co nghiem nguyen 
--------------- 
Voi dang phuong trinh nghiem nguyen bac 2 nay minh bay ban mot thu thuat phan h thanh nhan tu de lam, bat ky bai nao cung giai quyet duoc 
Vi du : Xet pt : 2x² - 2x + 3 = 2y² 
Buoc 1 : Chuyen ta ca cac hang tu co chua an sang mot ve 
2x² - 2x - 2y² = - 3 
Them vao 2 ve mot so a nao do 
2x² - 2x - 2y² + a = a - 3 
Xem ve trai la pt bac 2 an so x; tham so y can phan h thanh nhan tu. Muon vay delta phai la so chinh phuong

= 1 - 2(- 2y² + a) = 4y² + 1 - 2a 
De  la so chinhs phuong chon a = 1/2 =>  = 4y² 
Khi do tam thuc ve trai co 2 nghiem : x = (1 - 2y)/2; x = (1 + 2y)/2 
=> x + y - 1/2 = 0 va x - y - 1/2 = 0 
Vay tam thuc co the phan h thanh : (x + y - 1/2)(x - y - 1/2) = - 5/2 
hay (2x + 2y - 1)(2x - 2y - 1) = - 5

có đúng ko bn

Đáp án C