cho tam giác ABC có b2 + c2= 2a2
Chứng minh: góc BAC =< 60 độ
Cho tam giác ABC có góc A = 120 độ, BC = a, AC = b, AB = c. Chứng minh rằng a2 = b2 + c2 + bc ?
Kẻ đường cao BD ứng với AC. Do góc A tù \(\Rightarrow\) D nằm ngoài đoạn thẳng AC hay \(CD=AD+AC\) và \(\widehat{DAB}=180^0-120^0=60^0\)
Áp dụng định lý Pitago:
\(AB^2=BD^2+AD^2\) \(\Rightarrow BD^2=AB^2-AD^2\)
Trong tam giác vuông ABD:
\(cos\widehat{BAD}=\dfrac{AD}{AB}\Rightarrow\dfrac{AD}{AB}=cos60^0=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}AB\)
\(\Rightarrow BD^2=AB^2-\left(\dfrac{1}{2}AB^2\right)=\dfrac{3}{4}AB^2\)
Pitago tam giác BCD:
\(BC^2=BD^2+CD^2=\dfrac{3}{4}AB^2+\left(AD+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\left(\dfrac{1}{2}AB+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\dfrac{1}{4}AB^2+AB.AC+AC^2\)
\(=AB^2+AB.AC+AC^2\)
Hay \(a^2=b^2+c^2+bc\)
Cho tam giác ABC có AB = c; BC = a; AC = b . Nếu giữa a; b; c có liên hệ b2 + c2 = 2a2 thì độ dài đường trung tuyến xuất phát từ đỉnh A của tam giác tính theo a bằng:
A. a 3 2
B. a 3 3
C. a
D. 2a
Chọn A.
Hệ thức trung tuyến xuất phát từ đỉnh A của tam giác:
![]()
Mà b2 + c2 = 2a2 nên ![]() nên
nên ![]() .
.
Cho tam giác ABC có BAC = 60 độ , BAC < ABC . Trong góc ABC vẽ tia Bx sao cho CBx = 60 độ . Trên tia Bx lấy điểm D sao cho BD=BC . Trên cạnh AC lấy điểm E sao cho AB = AE . Chứng minh rằng tam giác BAD= tam giác BEC
Cho tam giác ABC có góc B =90 độ, vẽ trung truyến AM. Trên tia đối của MA lấy I sao cho MI=MA.
a)Chứng minh: Tam giác ABM=Tam giác ICM
b) Cho góc BAC =60 độ. Tính góc ACI =?
c) Chứng minh: 2AM<AB+AC
a) Xét ΔABM và ΔICM có
AM = MI (gt)
\(\widehat{AMB}=\widehat{CMI}\)(đối đỉnh)
BM=MC (AM là đường trung tuyến)
➩ ΔABM = ΔICM (c-g-c)
b) Xét ΔABC có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\\ 60^0+90^0+\widehat{C}=180^0\\ \widehat{C}=30^0\)
Mà \(\widehat{B}=\widehat{MCI}=90^0(ΔABM = ΔICM)\)
\(\Rightarrow\widehat{ACB}+\widehat{MCI}=\widehat{ACI}\\ 30^0+90^0=\widehat{ACI}\\ \widehat{ACI}=120^0 \)
c) Xét ΔACI có: AB + CI > AI (Bất đẳng thức trong tam giác)
hay AB + CI > AM + MI
AB + CI > 2AM
Mà AB = CI (ΔABM = ΔICM)
➩ AB + BA > 2AM (đpcm)
Cho tam giác ABC có góc BAC= 60 độ .các đường phân giác BE, CF cắt nhau tại I. Chứng minh rằng tam giác IEF cân.
c3
Cho Tam Giác ABC có Góc BAC = 60 độ và góc ABC =90 độ. tia phân giác góc BAC Cắt cạnh cắt cạnh BC tại D,từ D kẻ DE vuông góc với Ac(E Thuộc AC)
a)chứng minh Tam Giác ABD=AED
b) Chứng minh : EA=EC
c)Chứng Minh:DB<DC
d) Biết AC=2cm. tính AB;BC
a) Xét ΔABD vuông tại B và ΔAED vuông tại E có
AD chung
\(\widehat{BAD}=\widehat{EAD}\)(AD là tia phân giác của \(\widehat{BAE}\))
Do đó: ΔABD=ΔAED(cạnh huyền-góc nhọn)
b) Ta có: AD là tia phân giác của \(\widehat{BAC}\)(gt)
nên \(\widehat{DAC}=\dfrac{\widehat{BAC}}{2}=\dfrac{60^0}{2}=30^0\)(1)
Ta có: ΔABC vuông tại B(gt)
nên \(\widehat{C}+\widehat{A}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{DCA}+60^0=90^0\)
hay \(\widehat{DCA}=30^0\)(2)
Từ (1) và (2) suy ra \(\widehat{DAC}=\widehat{DCA}\)
Xét ΔDCA có \(\widehat{DAC}=\widehat{DCA}\)(cmt)
nên ΔDCA cân tại D(Định lí đảo của tam giác cân)
Suy ra: DA=DC(hai cạnh bên)
Xét ΔAED vuông tại E và ΔCED vuông tại E có
DA=DC(cmt)
DE chung
Do đó: ΔAED=ΔCED(cạnh huyền-cạnh góc vuông)
Suy ra: EA=EC(hai cạnh tương ứng)
c) Ta có: ΔABD=ΔAED(cmt)
nên BD=ED(Hai cạnh tương ứng)
mà ED<DC(ΔDEC vuông tại E có DC là cạnh huyền nên DC là cạnh lớn nhất)
nên DB<DC(Đpcm)
Cho tam giác ABC có 3 góc nhọn. Các đường cao BM, CN cắt nhau tại H
a) Chứng minh rằng: tam giác ABM đồng dạng với tam giác ACN và AN.AB=AM.AC
b) Chứng minh rằng: tam giác AMN đồng dạng với tam giác ABC
c) Giả sử góc BAC = 60 độ . Chứng minh diện tích tam giác ABC gấp 4 lần diện tích tam giác AMN
Mọi người giúp mình với nha!!!
a: Xét ΔABM vuông tại M và ΔACN vuông tại N có
góc BAM chung
=>ΔABM đồng dạng với ΔACN
=>AM/AN=AB/AC
=>AM*AC=AN*AB và AM/AB=AN/AC
b: Xét ΔAMN và ΔABC có
AM/AB=AN/AC
góc MAN chung
=>ΔAMN đòng dạng với ΔABC
c: ΔAMN đồng dạng với ΔABC
=>S AMN/S ABC=(AM/AB)^2=(cos60)^2=1/4
=>S ABC=4*S AMN
Trong tam giác ABC. Chứng minh rằng
a) Góc A nhọn khi và chỉ khi a2 < b2 + c2
b) Góc A tù khi và chỉ khi a2 > b2 + c2
c) Góc A vuông khi và chỉ khi a2 = b2 + c2
Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :
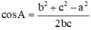
Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b2 + c2 – a2.
a) Góc A nhọn ⇔ cos A > 0 ⇔ b2 + c2 – a2 > 0 ⇔ a2 < b2 + c2.
b) Góc A tù ⇔ cos A < 0 ⇔ b2 + c2 – a2 < 0 ⇔ a2 > b2 + c2.
c) Góc A vuông ⇔ cos A = 0 ⇔ b2 + c2 – a2 = 0 ⇔ a2 = b2 + c2.
Cho tam giác ABC có góc BAC = 90 độ , AB < AC . Lấy K thuộc BC sao cho AB = BK . Gọi H là trung điểm của Ak , kéo dài BH cắt A tại J .
a, Biết góc ABC = 60 độ . Tính góc ACB
b, Chứng minh tam giác ABH = tam giác KBH , AK vuông góc BJ
c, d qua k , d // AC , d cắt AB tại D , d cắt BH tại N . Chứng minh KA là phân giác của góc JKD
Vẽ hình và giải giúp mình với ạ , mình đang cần gấp
Cho tam giác ABC có góc B bằng 60 độ ,2 tia phân giác AD và CF của các góc BAC,ADB cắt nhau tại E
.Chứng minh EF bằng ED