cho ∆ABC vuông tại a đường cao AH (H thuộc Bc) biết ACB =30° và BC=18cm tính АВ, АС, АН, ВН, HC

Những câu hỏi liên quan
Cho AABC vuông tại A, kẻ đường cao AH. Biết AC = 10cm, HC = 8cm. Tinh BC, АB, АН.
\(AH=\sqrt{AC^2-HC^2}=\sqrt{10^2-8^2}=6cm\)
\(HB=AH^2:HC=6^2:8=4,5cm\)
\(BC=HB+HC=4,5+8=12,5cm\)
\(AB=\sqrt{BC^2-AC^2}=\sqrt{12,5^2-10^2}=7,5cm\)
Đúng 1
Bình luận (0)
Cho \(\Delta\)ABC vuông tại A, đường cao AH (H thuộc BC). Biết AB:AC=5:12 và BC=26cm. Tính HC và HB.
\(\dfrac{AB}{AC}=\dfrac{5}{12}\Rightarrow AB=\dfrac{5}{12}AC\)
Áp dụng định lý Pitago:
\(AB^2+AC^2=BC^2\Leftrightarrow\left(\dfrac{5}{12}AC\right)^2+AC^2=26^2\)
\(\Rightarrow AC^2=576\Rightarrow AC=24\)
\(AB=\dfrac{5}{12}AC=10\)
Áp dụng hệ thức lượng:
\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{50}{13}\left(cm\right)\)
\(CH=BC-BH=\dfrac{288}{13}\left(cm\right)\)
Đúng 3
Bình luận (0)
Ta có: \(\left(\dfrac{AB}{AC}\right)^2=\dfrac{HB}{HC}\)
nên \(\dfrac{HB}{HC}=\dfrac{25}{144}\)
\(\Leftrightarrow HB=\dfrac{25}{144}HC\)
Ta có: HB+HC=BC(H nằm giữa B và C)
\(\Leftrightarrow HC\cdot\dfrac{169}{144}=26\)
\(\Leftrightarrow HC=\dfrac{288}{13}\left(cm\right)\)
\(\Leftrightarrow HB=\dfrac{25}{144}\cdot\dfrac{288}{13}=\dfrac{50}{13}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại a đường cao AH ( H thuộc BC) biết BH=4,3cm và HC=8,3cm tính Bc,AH,AB,AC
Cho tam giác ABC vuông tại A, AH là đường cao (H thuộc BC). Biết AB = 6cm, HC=6,4cm. Tính AH, AC,BC
Áp dụng hệ thức lượng:
\(AB^2=BH.BC=BH\left(BH+CH\right)\)
\(\Leftrightarrow36=BH\left(BH+6,4\right)\)
\(\Leftrightarrow BH^2+6,4BH-36=0\Rightarrow\left[{}\begin{matrix}BH=3,6\\BH=-10\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow BC=BH+CH=10\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
Áp dụng hệ thức lượng:
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=4,8\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho ΔABC vuông tại A, đường cao AH và đường phân giác AD (H và D thuộc BC). Biết AB = 21cm, AC = 28cm.
a) Tính diện tích tam giác ABC và chứng minh AH . BC = AB . AC
b) Tính độ dài BC, DB và DC.
c) Đường phân giác BK của ABC cắt AD tại I (K thuộc AC), tính tỉ số BI/IK . Gọi G là trọng tâm ΔABC, chứng minh IG //AC.
a: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot21\cdot28=294\left(cm^2\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\)
mà \(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\)
nên \(AH\cdot BC=AB\cdot AC\)
b: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=21^2+28^2=1225\)
=>\(BC=\sqrt{1225}=35\left(cm\right)\)
Xét ΔABC có AD là phân giác
nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)
=>\(\dfrac{DB}{15}=\dfrac{DC}{20}\)
=>\(\dfrac{DB}{3}=\dfrac{DC}{4}\)
mà DB+DC=BC=35cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{35}{7}=5\)
=>\(DB=5\cdot3=15\left(cm\right);DC=4\cdot5=20\left(cm\right)\)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A có đường cao AH ( H thuộc BC ) .Tính BH và HC ( biết AH = 4)
Cho ΔABC vuông tại A, đường cao AH và đường phân giác AD (H và D thuộc BC). Biết AB = 21cm, AC = 28cm.
a) Tính diện tích tam giác ABC và chứng minh AH . BC = AB . AC
b) Tính độ dài BC, DB và DC.
Trong ΔABC, ta có: AD là đường phân giác của (BAC)
Suy ra: 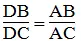 (tính chất đường phân giác)
(tính chất đường phân giác)
Mà AB = 21 (cm); AC = 28 (cm)
Nên \(\dfrac{DB}{DC}=\dfrac{AB}{AC}=\dfrac{21}{28}=\dfrac{3}{4}\)
Suy ra:
(tính chất tỉ lệ thức)Suy ra:
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho ΔABC vuông tại A, đường cao AH và đường phân giác AD (H và D thuộc BC). Biết AB = 21cm, AC = 28cm.
a) Tính diện tích tam giác ABC và chứng minh AH . BC = AB . AC
b) Tính độ dài BC, DB và DC.
c) Đường phân giác BK của góc ABC cắt AD tại I (K thuộc AC), tính tỉ số BI/IK. Gọi G là trọng tâm ΔABC, chứng minh IG //AC.
) Cho ΔABC vuông tại A, đường cao AH và đường phân giác AD (H và D thuộc BC). Biết AB = 21cm, AC = 28cm.
a) Tính diện tích tam giác ABC và chứng minh AH . BC = AB . AC
b) Tính độ dài BC, DB và DC.
c) Đường phân giác BK của ABC cắt AD tại I (K thuộc AC), tính tỉ số BI IK . Gọi G là trọng tâm ΔABC, chứng minh IG //AC.
















 hình vẽ
hình vẽ câu a)
câu a)




