Những câu hỏi liên quan
cho ba số x;y;z thỏa mãn:2x=3y;5y=7z;3x-7y+5z=-30. khi đó x+y+z=?
nhanh lên mk sắp hết thời gian rui giup vs cko han 5 like lun
+ \(2x=3y\Rightarrow x=\frac{3y}{2}\left(1\right)\)
+ \(5y=7z\Rightarrow z=\frac{5y}{7}\left(2\right)\)
Thay (1) và (2) vào 3x - 7y + 5z = - 30
Ta có \(3.\frac{3y}{2}-7y+5.\frac{5y}{7}=-30\Rightarrow y=-28\)
Thay y = - 28 vào (1) => x = - 42
Thay y = - 28 vào (2) => x = -20
Đúng 0
Bình luận (0)
\(\frac{x}{3}=\frac{y}{2};\frac{y}{7}=\frac{z}{5}\Rightarrow\frac{x}{21}=\frac{y}{14}=\frac{z}{10}=\frac{x+y+z}{21+14+10}=\frac{3x-7y+5z}{3.21-7.14+5.10}=-\frac{30}{15}=-2\)
\(\Rightarrow\frac{x+y+z}{45}=-2\Rightarrow x+y+z=-90\)
Đúng 0
Bình luận (0)
http://olm.vn/hoi-dap/question/280607.html
bạn tham khảo trang này nha
Đúng 0
Bình luận (0)
Bài 1: một canô xuôi khúc sông từ A đến B hết 2 giờ và ngược dòng khúc sông đó hết 3 giờ. Biet van toc cua dong nuoc la 3km/h.Tính quãng sông AB.
Bài 2: a) Tìm cặp số nguyên x,y thỏa mãn : 3x +4y - xy =15
b) cho các số nguyên a,b,c,d thỏa mãn: a+b=c+d và a^2 + b^2= c^2+ d^2.
Chung minh rang a^2014 +b^2014 = c^2014 +d^2014.
cho cặp số (x;y) thỏa mãn 2*(x^2+1)+x^2=2y(x+1) khi đó x+y=?
đặt x+y=a=> y=a-x
thay vào pt điều kiện
2(x^2+1)+x^2=2(a-x)(x+1)
3x^2+2 =2ax+2a-2x^2-2x
5x^2+2x-2ax+2-2a=0
5x^2+2(1-a)x+2(1-a)=0
(1-a)^2-10(1-a)>=0
(1-a)(1-a-10)>=0
(a-1)(a+9)>=0
a<=-9
hoặc
a>=1
(x+y)<-9 hoặc (x+y)>=1
Đúng 0
Bình luận (0)
Cho cặp số x,y thỏa mãn x/3=-y/7; xy=189 và x<y. Khi đó x=...........
x/3 = -y/7 ; xy = 189
- ; a/3 = -y/7 = k => x = 3k ; -y = 7k
Thay x = 3k ; -y = 7k vào xy = 189 ta có
3k.7k = 189
=> 21k2 = 189
k2 = 9 => k = -3 hoặc k = 3
k = 3 => x = 9 ; y = -21
k = -3 => x = -9 ; y = 21
Mà x < y => x = -9
Đúng 0
Bình luận (0)
Cho thỏa mãn
z
∈
C
thỏa mãn
2
+
i
z
10
z
+
1
-
2
i
. Biết tập hợp các điểm biểu diễn cho số phức
w
3
-
4
i
z
-
1
+
2...
Đọc tiếp
Cho thỏa mãn z ∈ C thỏa mãn 2 + i z = 10 z + 1 - 2 i . Biết tập hợp các điểm biểu diễn cho số phức w = 3 - 4 i z - 1 + 2 i là đường tròn I, bán kính R. Khi đó
A. I - 1 ; - 2 , R = 5
B. I 1 ; 2 , R = 5
C. I - 1 ; 2 , R = 5
D. I 1 ; - 2 , R = 5
Cho số phức z thỏa mãn
1
+
i
z
là số thực và
z
-
2
m
với m thuộc R Gọi
m
0
là một giá trị của m để có đúng một số phức thỏa mãn bài toán. Khi đó
Đọc tiếp
Cho số phức z thỏa mãn 1 + i z là số thực và z - 2 = m với m thuộc R Gọi m 0 là một giá trị của m để có đúng một số phức thỏa mãn bài toán. Khi đó
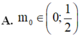
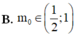
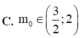
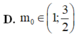
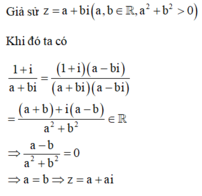
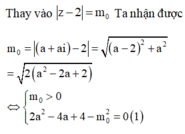
Để có đúng một nghiệm phức thỏa mãn bài toán thì phương trình (1) phải có duy nhất một nghiệm a. Khi đó phương trình (1) phải thỏa mãn

Đáp án D
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn
1
+
i
z
là số thực và |z-2|m với m
∈
R. Gọi
m
0
là một giá trị của m để có đúng một số phức thỏa mãn bài toán. Khi đó A.
m
0
∈
(
0
;
1
/
2
)
B. ...
Đọc tiếp
Cho số phức z thỏa mãn 1 + i z là số thực và |z-2|=m với m ∈ R. Gọi m 0 là một giá trị của m để có đúng một số phức thỏa mãn bài toán. Khi đó
A. m 0 ∈ ( 0 ; 1 / 2 )
B. m 0 ∈ ( 1 / 2 ; 1 )
C. m 0 ∈ ( 3 / 2 ; 2 )
D. m 0 ∈ ( 1 ; 3 / 2 )
Cho thỏa mãn
z
∈
ℂ
thỏa mãn
2
+
i
z
10
z
+
1
-
2
i
. Biết tập hợp các điểm biểu diễn cho số phức w ( 3 - 4i )z - 1 +2i là đường tròn I, bán kính R. Khi đó A. I ( -1;-2 ) R
5
B. I ( 1;2 ), R...
Đọc tiếp
Cho thỏa mãn z ∈ ℂ thỏa mãn 2 + i z = 10 z + 1 - 2 i . Biết tập hợp các điểm biểu diễn cho số phức w = ( 3 - 4i )z - 1 +2i là đường tròn I, bán kính R. Khi đó
A. I ( -1;-2 ) R = 5
B. I ( 1;2 ), R = 5
C. I ( -1;2 ), R = 5
D. I ( 1;-2 ), R= 5
2 + i z = 10 z + 1 - 2 i
⇔ 2 z - 1 + z + 2 i = 10 z 2 z
Bình phương modun của số thức bên trái và bên phải bằng nhau ta có:
⇔ 2 z - 1 + z + 2 i = 10 z 2 z
= 10 z 2 ⇔ 5 z 2 + 5 = 10 z 2 ⇒ z = 1
Đặt w = x + yi ⇒ w = (3 - 4i )z+2i
⇔ (x + 1 ) + ( y - 2 )i = ( 3 - 4i )z
⇒ x + 1 2 + y - 2 2 = 25
Vậy I ( -1;2 ), R = 5
Đáp án cần chọn là C
Đúng 0
Bình luận (0)
Cho a,b,c là các số nguyên thỏa mãn: a³+b³=2021c³. Chứng minh rằng: a+b+c chia hết cho 3
mn ơi mik cần gấp ngay bây giờ ạ!!
\(a^3+b^3=2021c^3\\ \Leftrightarrow a^3+b^3+c^3=2022c^3⋮6\left(2022⋮6\right)\left(1\right)\)
Mặt khác: \(\left(a^3+b^3+c^3\right)-\left(a+b+c\right)=\left(a-1\right)a\left(a+1\right)+\left(b-1\right)b\left(b+1\right)+\left(c-1\right)c\left(c+1\right)\)
Có \(\left(a-1\right)a\left(a+1\right);\left(b-1\right)b\left(b+1\right);\left(c-1\right)c\left(c+1\right)\) là 3 cặp số nguyên liên tiếp nên chia hết cho 6
Do đó \(\left(a^3+b^3+c^3\right)-\left(a+b+c\right)⋮6\)
Kết hợp (1) ta được đpcm
Đúng 0
Bình luận (0)