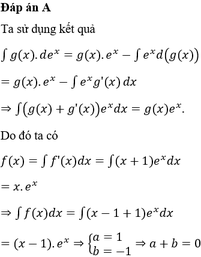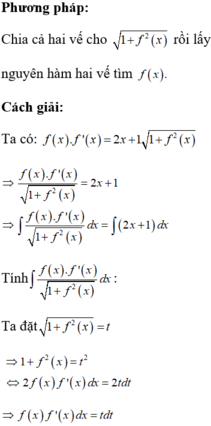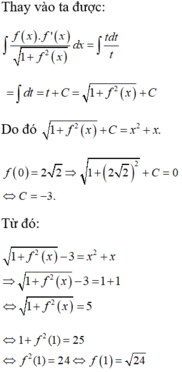cho hàm số f(x)=ax+b thỏa mãn đẳng thức f(f(f(0)))=1 và f(f(f(1))) =29 khi đó a=

Những câu hỏi liên quan
Cho hàm số f(x)=ax+b thỏa mãn đẳng thức
f(f(f(0)))=2 và f(f(f(1)))=29
Khi đó giá trị của a là bao nhiêu?
cho hàm số f(x)= ax+b thỏa mãn các đẳng thức f(f(f(0)))=2 và f(f(f(1)))=29.Khi đó giá trị của a là?
A-1
B-3
C-4
D-5
Cho hàm số f(x) có đạo hàm f(x) thỏa mãn các đẳng thức
∫
0
1
(
2
x
-
1
)
f
(
x
)
d
x
10
,
...
Đọc tiếp
Cho hàm số f(x) có đạo hàm f'(x) thỏa mãn các đẳng thức ∫ 0 1 ( 2 x - 1 ) f ' ( x ) d x = 10 , f ( 1 ) + f ( 8 ) = 0 . Tính I = ∫ 0 1 f ( x ) d x .
A. I = 2.
B. I = 1.
C. I = -1.
D. I = -2.
Cho hàm số y f(x) thỏa mãn f(x)
(
x
+
1
)
e
x
và
∫
f
(
x
)
d
x
(
a
x
+
b
)
e
x
+
c
, với a, b, c là các hằng số. Khi đó A. a + b 0 B. a + b 3 C. a + b 2 D. a + b 1
Đọc tiếp
Cho hàm số y = f(x) thỏa mãn f'(x) = ( x + 1 ) e x và ∫ f ( x ) d x = ( a x + b ) e x + c , với a, b, c là các hằng số. Khi đó
A. a + b = 0
B. a + b = 3
C. a + b = 2
D. a + b = 1
Cho hàm số yf(x) thỏa mãn
f
(
x
)
(
x
+
1
)
e
x
và
∫
f
(
x
)
d
x
(
a
x
+
b
)
e
x
+
c
với a, b, c là các hằng số. Khi đó: A. a + b 0 B. a + b 3 C. a + b 2 D. a + b 1
Đọc tiếp
Cho hàm số y=f(x) thỏa mãn f ' ( x ) = ( x + 1 ) e x và ∫ f ( x ) d x = ( a x + b ) e x + c với a, b, c là các hằng số. Khi đó:
A. a + b = 0
B. a + b = 3
C. a + b = 2
D. a + b = 1
Cho f(x)=\(\text{ax}+b\)thoả mãn f(f(f(0)))=2 và f(f(f(1)))=29. Khi đó giá trị của a là:
\(f\left(0\right)=b;f\left(b\right)=ab+b;f\left(f\left(b\right)\right)=a^2b+b=2\)
\(f\left(1\right)=a+b;f\left(f\left(1\right)\right)=a\left(a+b\right)+b;f\left(f\left(f\left(1\right)\right)\right)=a\left(a\left(a+b\right)\right)+b=29\)
\(\hept{\begin{cases}a^2b+b=2\\a^3+a^2b+b=29\end{cases}}\Rightarrow a^3=27\Rightarrow\hept{\begin{cases}a=3\\b=\frac{1}{5}\end{cases}}\Rightarrow f\left(x\right)=3x+\frac{1}{5}\)
Đúng 0
Bình luận (0)
ngonhuminh làm sai mà vẫn cho là đúng???
Cẩn thận \(f\left(f\left(f\left(1\right)\right)\right)=f\left(f\left(a+b\right)\right)=f\left(a\left(a+b\right)+b\right)=a\left[a\left(a+b\right)+b\right]+b\)
Đúng 0
Bình luận (0)
Cho hàm số f(x) thỏa mãn f'(x) + 2x.f(x) = f(x).lnx với f(x)≠ 0, ∀x và f(1) =1. Khi đó \(\left|f\left(2\right)\right|\) bằng ?
\(\Leftrightarrow\dfrac{f'\left(x\right)}{f\left(x\right)}+2x=lnx\Rightarrow\dfrac{f'\left(x\right)}{f\left(x\right)}=lnx-2x\)
Lấy nguyên hàm 2 vế:
\(\Rightarrow\int\dfrac{f'\left(x\right)}{f\left(x\right)}dx=\int\left(lnx-2x\right)dx\)
\(\Rightarrow ln\left|f\left(x\right)\right|=x\left(lnx-1\right)-x^2+C\)
Thay \(x=1\)
\(\Rightarrow ln\left|f\left(1\right)\right|=-2+C\Rightarrow C=2\)
\(\Rightarrow ln\left|f\left(x\right)\right|=x\left(lnx-1\right)-x^2+2\)
\(\Rightarrow\left|f\left(x\right)\right|=e^{x\left(lnx-1\right)-x^2+2}\)
\(\Rightarrow\left|f\left(2\right)\right|\)
Đúng 2
Bình luận (0)
T Nc cđ :
Bài 2: Cho đa thức f(x) thỏa mãn điều kiện: x.f(x + 1) = (x + 2).f(x). Chứng minh rằng đa thức f(x) có ít nhất hai nghiệm.
Bài 3: Cho hàm số f(x) = ax^2 + bx + c (a, b, c ∈ Z}). Biết f(-1) ⋮ 3; f(0) ⋮ 3; f(1) ⋮ 3. Chứng minh rằng a, b, c đều chia hết cho 3.
Bài 4: Cho đa thức f(x) = ax^3 + bx^2 + cx + d với a là số nguyên dương và f(5) - f(4) = 2019. Chứng minh f(7) - f(2) là hợp số.
Bài 4:
\(f\left(5\right)-f\left(4\right)=2019\)
=>\(125a+25b+25c+d-64a-16b-4c-d=2019\)
=>\(61a+9b+21c=2019\)
\(f\left(7\right)-f\left(2\right)\)
\(=343a+49b+7c+d-8a-4b-2c-d\)
\(=335a+45b+5c\)
\(=5\left(61a+9b+21c\right)=5\cdot2019\) là hợp số
Đúng 0
Bình luận (0)
Cho hàm số f(x) liên tục trên R thỏa mãn điều kiện:
f
(
0
)
2
3
,
f
(
x
)
0
,
∀
x
∈
ℝ
và
f
(
x
)
.
f
(
x
)
(
2
x
+
1
)
1
+
f...
Đọc tiếp
Cho hàm số f(x) liên tục trên R thỏa mãn điều kiện: f ( 0 ) = 2 3 , f ( x ) > 0 , ∀ x ∈ ℝ và f ( x ) . f ' ( x ) = ( 2 x + 1 ) 1 + f 2 ( x ) , ∀ x ∈ ℝ . Khi đó giá trị f(1) bằng:
![]()
![]()
![]()
![]()