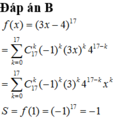tổng tất cả các hệ số trong khai triển \(\left(3x-4\right)^{17}\)là bao nhiêu

Những câu hỏi liên quan
Biết tổng các hệ số của khai triển \(\left(3-x^2\right)^n\)bằng 1024. Hệ số của số hạng chứa \(x^{12}\) trong khai triển đó bằng bao nhiêu?
\(\left(3-1\right)^n=1024\Leftrightarrow2^n=2^{10}\Rightarrow n=10\)
\(\left(3-x^2\right)^{10}\) có SHTQ: \(C_{10}^k.3^k.\left(-1\right)^{10-k}.x^{20-2k}\)
Số hạng chứa \(x^{12}\Rightarrow20-2k=12\Rightarrow k=4\)
Hệ số: \(C_{10}^4.3^4=...\)
Đúng 1
Bình luận (1)
Tính tổng S tất cả các hệ số trong khai triển 3 x - 4 17
A. S = 1
B. S = -1
C. S = 0
D. S = 8192
Tính tổng các hệ số trong khai triển => cho x = 1
Khi đó ![]() Chọn B.
Chọn B.
Đúng 0
Bình luận (0)
Tính tổng S tất cả các hệ số trong khai triển
3
x
−
4
17
.
A. S 1 B. S -1 C. S 0 D. S 8192
Đọc tiếp
Tính tổng S tất cả các hệ số trong khai triển 3 x − 4 17 .
A. S = 1
B. S = -1
C. S = 0
D. S = 8192
Đáp án B
f ( x ) = 3 x - 4 17 = ∑ k = 0 17 C 17 k - 1 k 3 x k 4 17 − k = ∑ k = 0 17 C 17 k 4 17 − k x k S = f ( 1 ) = - 1 17 = − 1
Đúng 0
Bình luận (0)
Tính tổng S tất cả các hệ số trong khai triển 3 x - 4 17
A. 1
B. -1
C. 0
D. 8192
tổng các hệ số nhị thức niuton trong khai triển \(\left(2nx+\frac{1}{2nx^2}\right)^{3n}\) bằng 64 . số hạng không chứa x trong khai triển là bao nhiêu ?
ta có : \(\left(2nx+\dfrac{1}{2nx^2}\right)^{3n}=\sum\limits^{3n}_{k=0}C^k_{3n}\left(2nx\right)^{3n-k}\left(\dfrac{1}{2nx^2}\right)^k\)
\(=\sum\limits^{3n}_{k=0}C^k_{3n}2^{3n-2k}\left(n\right)^{3n-2k}\left(x\right)^{3n-3k}\)
\(\Rightarrow\) tổng hệ số bằng : \(C^0_{3n}+C_{3n}^1+C^2_{3n}+...+C^{3n}_{3n}=64\)
\(\Leftrightarrow\left(1+1\right)^{3n}=64\Leftrightarrow2^{3n}=2^6\Rightarrow n=2\)
để có số hạng không chữa \(x\) không khai triển thì \(3n-3k=0\Leftrightarrow n=k\)
\(\Rightarrow\) hệ số của số hạng không chữa \(x\) là \(C^2_6.2^2.2^2=240\)
vậy ...........................................................................................................................
Đúng 0
Bình luận (0)
Từ khai triển biểu thức \(\left(3x-4\right)^{17}\) thành đa thức, hãy tính tổng các hệ số của đa thức nhận được ?
Tổng các hệ số của đa thức f(x) = (3x – 4)17 bằng:
f(1) = (3 – 4)17= (– 1)17 = -1
Đúng 0
Bình luận (1)
Tính tổng các hệ số của tất cả các hạng tử trong khai triển của nhị thức (3x−5y)20
tính tổng các hệ số của tất cả các hạng tử trong khai triển
a) (5x - 3)^6
b) (3x - 4y)^20
a, Thay x = 1 ta có
a, ( 5.1 - 3)^2 = 2^ 2 = 4
VẬy tổng các hệ số là 4
b thay x = 1 ; y = 1 ta có:
( 3.1 - 4.1 )^20 = (-1)^20 = 1
(*) Tổng quát muố tính tổng các hệ số sau khi khai chuyển ta chỉ việc thay 1 vào
Đúng 0
Bình luận (0)
mk ko nghĩ như vậy khi khai triển theo pascal kết quả hoàn toàn khác
Đúng 0
Bình luận (0)
\(5x^3+7x^2+6x+5=0\)
\(\Delta'=\sqrt{8}-5.\sqrt{5}=\sqrt{90}\)
\(pt\Leftrightarrow\left(4+5x\right)\left(9b+b\right)=0\)
\(\Leftrightarrow\sqrt{10}=\sqrt{6}\)
Đúng 0
Bình luận (0)
Cho khai triển
1
+
x
2
n
biết tổng của tất cả các hệ số trong khai triển đã cho bằng 1024. Tìm n. A. n 9 B. n 10 C. n 11 D. n 12
Đọc tiếp
Cho khai triển 1 + x 2 n biết tổng của tất cả các hệ số trong khai triển đã cho bằng 1024. Tìm n.
A. n = 9
B. n = 10
C. n = 11
D. n = 12