Cho y = f(x) = x2 + 2x
Tìm x biết f(x) = 0
Những câu hỏi liên quan
y=f(x)=5-2x
tìm x để :y=5,y=3,y=-1
để y=5
⇒ 5-2x=5 ⇒x=0
để y=3
⇒ 5-2x=3 ⇒ x=1
để y=-1
⇒ 5-2x=-1 ⇒x=3
Đúng 0
Bình luận (0)
Cho hàm số y=f(x) xác định với mọi x khác 0. Biết f(1)=1; f(1) : x = 1/x^2 * f(x). Biết f(x1+x2) = f(x1) + f(x2) với x(1) và x(2) khác 0. Tính f(2014/2015)
Bài 5: Cho hàm số y=f(x)≠0y=f(x)≠0 (∀x∈R;x≠0∀x∈R;x≠0) có tính chất f(x1,x2)=f(x1).f(x2)f(x1,x2)=f(x1).f(x2) . Hãy chứng minh rằng:
a) f(1)=1f(1)=1 b) f(x−1)=[f(x)]−1
giúp mình phần b với!
Cho hàm số y f (x) liên tục trên R có đồ thị như hình vẽ. Biết trên
(
-
∞
;
-
3
)
∪
(
2
;
+
∞
)
t
h
ì
f
(
x
)
0
. Số nghiệm nguyên thuộc (-10; 10) của bất phương trình
[
f
(
x
)...
Đọc tiếp
Cho hàm số y = f (x) liên tục trên R có đồ thị như hình vẽ.
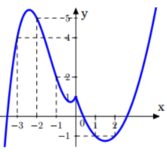
Biết trên ( - ∞ ; - 3 ) ∪ ( 2 ; + ∞ ) t h ì f ' ( x ) > 0 . Số nghiệm nguyên thuộc (-10; 10) của bất phương trình [ f ( x ) + x - 1 ] ( x 2 - x - 6 ) > 0 là
A. 9
B. 10
C. 8
D. 7
Cho hàm số yf(x) có đạo hàm
f
(
x
)
x
2
(
x
-
1
)
(
x
-
4
)
g
(
x
)
, trong đó
g
(
x
)
0
,
∀
x
. Hàm số
y
f
(
x
2...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x 2 ( x - 1 ) ( x - 4 ) g ( x ) , trong đó g ( x ) > 0 , ∀ x . Hàm số y = f ( x 2 ) đồng biến trên khoảng nào dưới đây?
A. ( - ∞ ; - 2 ) .
B. (-1;1).
C. (-2;-1).
D. (1;2).
Cho hàm số y = f(x) = x2 + 4x. Tìm số nghiệm của phương trình: f(f(x) + x2) + 3 = 0.
\(f\left(f\left(x\right)+x^2\right)+3=0\)
=>\(f\left(x^2+4x+x^2\right)+3=0\)
=>\(f\left(2x^2+4x\right)+3=0\)
=>\(\left(2x^2+4x\right)^2+4\left(2x^2+4x\right)+3=0\)
=>\(\left(2x^2+4x+1\right)\left(2x^2+4x+3\right)=0\)
=>\(\left[{}\begin{matrix}2x^2+4x+1=0\\2x^2+4x+3=0\end{matrix}\right.\Leftrightarrow x=\dfrac{-2\pm\sqrt{2}}{2}\)
Đúng 0
Bình luận (0)
Cho hàm số bậc 4 y f(x) có đồ thị như hình vẽ bên. Biết hàm số y f(x) đạt cực trị tại các điểm x1,x2,x3 thỏa mãn x3 x1+2, f(x1) + f(x3) +dfrac{2}{3}f(x2) 0 và (C) nhận đường thẳng x x2 làm trục đối xứng. Gọi S1,S2,S3,S4 là diện tích của các miền hình phẳng được đánh dấu như hình bên. Tỉ số dfrac{S_1+S_2}{S_3+S_4} gần với kết quả nào nhất :
Đọc tiếp
Cho hàm số bậc 4 y = f(x) có đồ thị như hình vẽ bên. Biết hàm số y = f(x) đạt cực trị tại các điểm x1,x2,x3 thỏa mãn x3 = x1+2, f(x1) + f(x3) +\(\dfrac{2}{3}\)f(x2) = 0 và (C) nhận đường thẳng x = x2 làm trục đối xứng. Gọi S1,S2,S3,S4 là diện tích của các miền hình phẳng được đánh dấu như hình bên. Tỉ số \(\dfrac{S_1+S_2}{S_3+S_4}\) gần với kết quả nào nhất :
Có thể nghịch suy để chọn hàm làm trắc nghiệm
Do \(x_2=\dfrac{x_3-x_1}{2}=1\) nên hàm có dạng: \(y=a\left(x-1\right)^4-b\left(x-1\right)^2+c\) với a;b;c dương
\(y'=0\Rightarrow\left[{}\begin{matrix}x-1=0\\\left(x-1\right)^2=\dfrac{b}{2a}\end{matrix}\right.\) \(\Rightarrow x_1;x_3\) thỏa mãn \(\left(x-1\right)^2=\dfrac{b}{2a}\) và \(f\left(x_2\right)=c\)
\(f\left(x_1\right)+f\left(x_3\right)+\dfrac{2}{3}f\left(x_2\right)=0\Leftrightarrow2f\left(x_1\right)+\dfrac{2}{3}f\left(x_2\right)=0\)
\(\Leftrightarrow a.\left(\dfrac{b}{2a}\right)^2-b\left(\dfrac{b}{2a}\right)+c+\dfrac{c}{3}=0\Rightarrow-\dfrac{b^2}{4a}+\dfrac{4c}{3}=0\)
Tới đây chọn \(a=3;c=1;b=4\) được hàm \(f\left(x\right)=3\left(x-1\right)^4-4\left(x-1\right)^2+1\)
Dễ dàng tính ra \(x_3=1+\sqrt{\dfrac{2}{3}}\) ; \(x_0=1+\sqrt{\dfrac{1}{3}}\) (với \(x_0\) là giao bên phải của đồ thị và trục hoành); \(f\left(x_1\right)=f\left(x_3\right)=-\dfrac{1}{3}\)
\(S_1+S_2=\int\limits^{x_0}_1f\left(x\right)dx-\int\limits^{x_3}_{x_0}f\left(x\right)dx\approx0,41\)
\(\dfrac{S_1+S_2}{S_3+S_4}=\dfrac{0,41}{\left(1+\dfrac{1}{3}\right)\left(x_3-1\right)-0,41}\approx0,6\)
Đúng 1
Bình luận (0)
Cho hàm số y f(x) có đạo hàm liên tục trên đoạn [-3;3] và đồ thị y f’(x) như hình vẽ. Đặt
g
x
2
f
x
+
x
2
+
4
. Biết f(1)-24. Hỏi g(x) 0 có bao nhiêu nghiệm thực? A. 1 B. 4 C. 2 D. 0
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm liên tục trên đoạn [-3;3] và đồ thị y = f’(x) như hình vẽ. Đặt g x = 2 f x + x 2 + 4 . Biết f(1)=-24. Hỏi g(x) = 0 có bao nhiêu nghiệm thực?
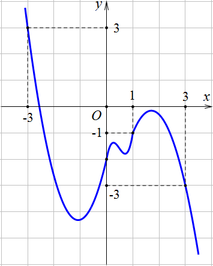
A. 1
B. 4
C. 2
D. 0
cho hàm số: y= f(x)= ax^2. biết rằng x = -2 thì y = -3/4
a) tìm hệ số a
b) tính f( -1,5); f(0,5)
c) biết rằng x1 , x2 là những số âm và x1 < x2. hãy so sánh f(x1) và f(x2)
d) biết rằng x1< 0< x2 và f(x1)> f(x2). hãy so sánh | x1|, | x2|
cho hàm số: y= f(x)= ax^2. biết rằng x = -2 thì y = -3/4
a) tìm hệ số a
b) tính f( -1,5); f(0,5)
c) biết rằng x1 , x2 là những số âm và x1 < x2. hãy so sánh f(x1) và f(x2)
d) biết rằng x1< 0< x2 và f(x1)> f(x2). hãy so sánh | x1|, | x2|