tham khảo nha bn

Ông cha ta có câu: “Một lần bất tín, vạn lần bất tin”. Một trong những điều khiến cho chúng ta đánh mất đi lòng tin của người khác chính là việc nói dối. Nói dối có tác hại to lớn trong cuộc sống của con người.

Ông cha ta đã có câu: “Một lần bất tín, vạn lần bất tin”. Một trong những điều mà khiến cho chúng ta đánh mấtlòng tin của người khác chính là việc nói dối. Nói dối nó có tác hại rất là to lớn trong cuộc sống của mỗi con người.

\(\Delta DAC\sim\Delta DBA\left(g.g\right)\Rightarrow\dfrac{AC}{BA}=\dfrac{DA}{DB}\). (1)

\(\Delta DFC\sim\Delta DBF\left(g.g\right)\Rightarrow\dfrac{FC}{BF}=\dfrac{DF}{DB}\). (2)

Lại có DA = DF (3) (tính chất hai tiếp tuyến cắt nhau)

Từ (1), (2), (3) suy ra \(\dfrac{AC}{BA}=\dfrac{FC}{BF}\Rightarrow AC.BF=FC.BA\).

Áp dụng định lý Ptoleme cho tứ giác ABFC nội tiếp ta có AC . BF + FC . BA = BC . AF

\(2.AC.BF=BC.2FH\Rightarrow AC.BF=BC.FH\Rightarrow\dfrac{AC}{BC}=\dfrac{FH}{FB}\Rightarrow\Delta BCA\sim\Delta BFH\left(c.g.c\right)\Rightarrow\dfrac{BA}{BC}=\dfrac{BH}{BF}\Rightarrow BH.BC=BA.BF=2OC.BF\).

P/s: Đây là tính chất kinh điển của tứ giác điều hòa

a: Gọi giao điểm của AG với BC là E

Xét ΔABD có

G là trọng tâm

E là giao điểm của AG với BD

Do đó: E là trung điểm của BD và AG=2/3AE

Xét ΔAHD có \(\dfrac{AG}{AE}=\dfrac{AM}{AD}=\dfrac{2}{3}\)

nên GM//ED

=>GM//BD

mà BD\(\subset\left(BCD\right)\) và GM không thuộc mp(BCD)

nên GM//(BCD)

b: Gọi giao của AH với BC là F

Xét ΔABC có

H là trọng tâm

F là giao điểm của AH với BC

Do đó: F là trung điểm của BC và AH=2/3AF

Xét ΔAGE có \(\dfrac{AH}{AF}=\dfrac{AG}{AE}=\dfrac{2}{3}\)

nên HG//FE

mà \(FE\subset\left(BCD\right)\);HG không thuộc(BCD)

nên HG//(BCD)

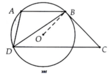
Chứng minh được: ∆DBC:∆BAD =>  D B C ^ = B A D ^

=>  s đ D B C ⏜ = 1 2 s đ B m D ⏜

=> BC là tiếp tuyến của (O)

tớ lại làm đề ăn quả nhớ kẻ trồng cây cơ

mà cậu lên google mà hỏi ý, cả đống bài

Tính chất: Trong hình thoi, đường chéo này là trung trực của hai cạnh AB và AC. Nên E là tâm đường tròn ngoại tiếp của ∆ABC. Tương tự, F là tâm đường tròn ngoại tiếp của ∆ABD

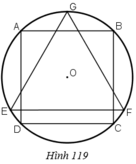
Dựng GH vuông góc EF.

Khi hình vẽ quay quanh trục GO thì:

Ta có:

AB = BC

Thể tích hình trụ sinh ra bởi hình vuông ABCD là:

Thể tích hình nón: