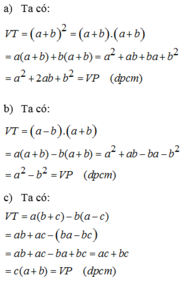CmR: nếu a2 + b2 =2ab thì a=b

Những câu hỏi liên quan
Để tính giá trị biểu thức 20212 – 212 theo phương pháp dùng hằng đẳng thức thì áp dụng hằng đẳng thức nào sau đây?A. (A – B)2 A2 – 2AB + B2 B. (A + B)2 A2 + 2AB + B2C. A2 – B2 (A + B)(A – B) D. A3 – B3 (A – B)(A2 + AB + B2)
Đọc tiếp
Để tính giá trị biểu thức 20212 – 212 theo phương pháp dùng hằng đẳng thức thì áp dụng hằng đẳng thức nào sau đây?
A. (A – B)2 = A2 – 2AB + B2
B. (A + B)2 = A2 + 2AB + B2
C. A2 – B2 = (A + B)(A – B)
D. A3 – B3 = (A – B)(A2 + AB + B2)
Câu 6: ( 0,5 điểm)
Chứng minh rằng nếu a, b, c là ba cạnh của một tam giác thì:
a2+ b2+ c2 - 2ab -2bc- 2ac < 0
Vì a,b,c là 3 cạnh tam giác nên \(a+b>c\Leftrightarrow ac+bc>c^2\)
CMTT: \(ab+bc>b^2;ab+ac>a^2\)
Cộng vế theo vế \(\Leftrightarrow a^2+b^2+c^2< ab+bc+ca+ab+bc+ca\)
\(\Leftrightarrow a^2+b^2+c^2< 2ab+2bc+2ca\\ \Leftrightarrow a^2+b^2+c^2-2ab-2bc-2ca< 0\)
Đúng 0
Bình luận (0)
Biến đổi vế trái thành vế phải:a)
a
+
b
2
a
2
+
2
a
b
+
b
2
b)
(
a
−
b
)
(
a
+
b
)
a
2
−
b
2
c...
Đọc tiếp
Biến đổi vế trái thành vế phải:
a) a + b 2 = a 2 + 2 a b + b 2
b) ( a − b ) ( a + b ) = a 2 − b 2
c) a ( b + c ) − b ( a − c ) = ( a + b ) c
a, a(b+c)−b(a−c)a(b+c)−b(a−c)
=ab+ac−(ab−bc)=ab+ac−(ab−bc)
=ab+ac−ab+bc=ab+ac−ab+bc
=ac+bc=ac+bc
=(a+b)c=(a+b)c
b,(a+b)(a−b)(a+b)(a−b)
=(aa+ab)−(ab+bb)=(aa+ab)−(ab+bb)
=aa+ab−ab−bb
Chứng tỏ rằng với a và b là các số bất kì thì: a 2 + b 2 - 2 a b ≥ 0
Ta có: a - b 2 ≥ 0 ⇒ a 2 + b 2 - 2 a b ≥ 0
Đúng 0
Bình luận (0)
CMR :1,a2+b2=<a+b>2-2ab
2,a3+b3=<a+b>3-3ab.<a+b>
3,a3-b3=<a-b>3+3ab.<a+b>
Cho :a+b=1
Tính :A=a3+b3+3ab
2
Ta có:
VP=(a+b)3−3ab(a+b)VP=(a+b)3-3ab(a+b)
=a3+b3+3ab(a+b)−3ab(a+b)=a3+b3+3ab(a+b)-3ab(a+b)
=a3+b3=VT(dpcm)
Đúng 0
Bình luận (0)
1, \(VT=a^2+b^2=a^2+b^2+2ab-2ab=\left(a+b\right)^2-2ab=VP\left(đpcm\right)\)
Đúng 0
Bình luận (0)
chứng minh các đẳng thức sau
(a-b)2=a2-2ab+b2
(a-b)(a+b)=a2-b2
(a+b)3=a3+3a2b+3ab2+b3
(a-b)^2=(a-b)(a-b)=a^2-ab-ab+b^2=a^2-2ba+b^2
(a-b)(a+b)=a^2+ab-ab-b^2=a^2-b^2
(a+3)^3=(a+b)^2*(a+b)
=(a^2+2ab+b^2)(a+b)
=a^3+a^2b+2a^2b+2ab^2+b^2a+b^3
=a^3+3a^2b+3ab^2+b^3
Đúng 1
Bình luận (0)
Chúng mình đã biết công thức (a + b)2 = a2 + 2ab + b2, còn công thức tính (a + b)3 thì sao nhỉ?
\(\left(a+b\right)^3=\left(a+b\right)^2\cdot\left(a+b\right)\)
\(=\left(a^2+2ab+b^2\right)\left(a+b\right)\)
\(=a^3+a^2b+2a^2b+2ab^2+ab^2+b^3\)
\(=a^3+3a^2b+3ab^2+b^3\)
Đúng 1
Bình luận (0)
Nếu a1b1=a2b2 thì: A. a1/a2=b1/b2 B. a1/a2=b2/b1 C. a1/b2=a2/b1 D. a1/b2=b1/a2
GYE4F4GGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGG
Đúng 0
Bình luận (0)
a/. a4 + b4 ≥ 2a2b2
b/. (a2 + b2)2 ≥ 2a3b + 2ab3
c/. a2 - b2 ≥ 2ab (a - b)
d/. (a + b)2 ≥ 4ab
Mọi người giupps em với ạ :((
a: \(a^4+b^4\ge2a^2b^2\)
\(\Leftrightarrow a^4-2a^2b^2+b^4>=0\)
hay \(\left(a^2-b^2\right)^2\ge0\)(luôn đúng)
d: \(\left(a+b\right)^2\ge4ab\)
\(\Leftrightarrow a^2+2ab+b^2-4ab\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\)(luôn đúng)
Đúng 2
Bình luận (0)
cho 2 số a,b thỏa: a2-2ab+1=2(ab-b2)
tinhsP= \(\dfrac{a^5+b^5+2ab}{4a^3-2ab}\)