giai hpt
x^2-4y=2
3x+3y=1
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
a ) 4 x − 4 y = 2 − 2 x + 2 y = − 1 b ) 1 3 x − y = 2 3 x − 3 y = 2
a)
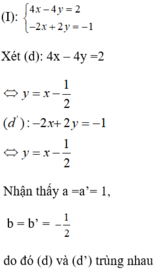
Vậy hệ phương trình có vô số nghiệm.
b)
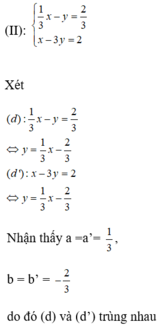
Vậy hệ phương trình có vô số nghiệm.
Kiến thức áp dụng
+ Xét hệ (I): 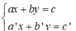
Gọi (d): ax + b = c và (d’): a’x + b’ = c’.
Số nghiệm của hệ (I) phụ thuộc vào vị trí tương đối của (d) và (d’).
(d) cắt (d’) ⇒ hệ (I) có nghiệm duy nhất.
(d) // (d’) ⇒ hệ (I) vô nghiệm
(d) ≡ (d’) ⇒ hệ (I) có vô số nghiệm.
+ Cho đường thẳng (d): y = ax + b và (d’): y = a’x + b’.
(d) cắt (d’) ⇔ a ≠ a’
(d) // (d’) ⇔ a = a’ và b ≠ b’
(d) trùng (d’) ⇔ a = a’ và b = b’
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
a ) x + y = 2 3 x + 3 y = 2 b ) 3 x − 2 y = 1 − 6 x + 4 y = 0
a) (I): 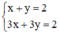
Xét (d): x + y = 2 hay (d): y = -x + 2 có a = -1; b = 2.
(d’) 3x + 3y = 2 hay (d’): y = -x + 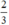 có a’ = -1 ; b’ =
có a’ = -1 ; b’ = 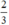
Ta có: a = a’ ; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ (I) vô nghiệm.
b) (II): 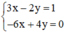
Xét: (d): 3x – 2y = 1 hay (d):
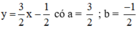
(d’): -6x + 4y = 0 hay (d’):
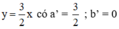
Ta có: a = a’ ; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ (II) vô nghiệm.
Kiến thức áp dụng
+ Xét hệ (I): 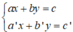
Gọi (d): ax + by = c và (d’): a’x + b’y = c’.
Số nghiệm của hệ (I) phụ thuộc vào vị trí tương đối của (d) và (d’).
(d) cắt (d’) ⇒ hệ (I) có nghiệm duy nhất.
(d) // (d’) ⇒ hệ (I) vô nghiệm
(d) ≡ (d’) ⇒ hệ (I) có vô số nghiệm.
+ Cho đường thẳng (d): y = ax + b và (d’): y = a’x + b’.
(d) cắt (d’) ⇔ a ≠ a’
(d) // (d’) ⇔ a = a’ và b ≠ b’
(d) trùng (d’) ⇔ a = a’ và b = b’.
Giai phương trình nghiệm nguyên :
\(\frac{11x}{5}-\sqrt{2x+1}=3y-\sqrt{4y}-1+2\)
\(\frac{11x}{5}-\sqrt{2x+1}=3y-\sqrt{4y-1}+2\)
\(\Leftrightarrow\sqrt{4y-1}-\sqrt{2x+1}=3y+2-\frac{11x}{5}\)
Vì 4y - 1 chia cho 4 có số dư là 2 nên \(\sqrt{4y-1}\)là số vô tỷ .
Ta có VP là số hữu tỉ. VT là số vô tỷ và \(\hept{\begin{cases}4y-1\\2x+1\end{cases}}\)là 2 số hữu tỷ nên.
\(\Rightarrow\sqrt{4y-1}-\sqrt{2x+1}=0\)
\(\Leftrightarrow x=2y-1\)
Thế lại phương trình ban đầu ta được.
\(\Rightarrow y=3\)
\(\Rightarrow x=5\)
Vậy nghiệm cần tìm là \(\hept{\begin{cases}x=5\\y=3\end{cases}}\)
11x5 −√2x+1=3y−√4y−1+2
⇔√4y−1−√2x+1=3y+2−11x5
Vì 4y - 1 chia cho 4 có số dư là 2 nên √4y−1là số vô tỷ .
Ta có VP là số hữu tỉ. VT là số vô tỷ và {
| 4y−1 |
| 2x+1 |
là 2 số hữu tỷ nên.
⇒√4y−1−√2x+1=0
⇔x=2y−1
Thế lại phương trình ban đầu ta được.
⇒y=3
⇒x=5
Vậy nghiệm cần tìm là {
| x=5 |
| y=3 |
@alibaba_nguyễn chép sai đề rồi kìa bạn
kết quả phép chia (25x^5y - 20x^3y^2 - 5x^3y) : 5x^3y là:
A.5x^2y - 4y - x B.5x^2 + 4y C. 5x^2 - 4y D.5x^2 - 4y - 1
a)-6x^3y^2:2xy^2. b)-1/4x^4y^3:1/2x^3y^2. c) 8x^4y^5:4x^3y^4
a: \(=\left(-\dfrac{6}{2}\right)\cdot\dfrac{x^3}{x}\cdot\dfrac{y^2}{y^2}=-3x^2\)
b: \(=\left(-\dfrac{1}{4}:\dfrac{1}{2}\right)\cdot\dfrac{x^4}{x^3}\cdot\dfrac{y^3}{y^2}=-\dfrac{1}{2}xy\)
c: \(=\dfrac{8}{4}\cdot\dfrac{x^4}{x^3}\cdot\dfrac{y^5}{y^4}=2xy\)
\(a,-6x^3y^2:2xy^2=-3x^2\)
\(b,-\dfrac{1}{4}x^4y^3:\dfrac{1}{2}x^3y^2=-\dfrac{1}{2}xy\)
\(c,8x^4y^5:4x^3y^4=2xy\)
#Urushi
giai he pt:
x-3y=4y/x
y-3x=4x/y
1)4x^5y^2-8x^4y^2+4x^3y^2 2)5x^4y^2-10x^3y^2+5x^2y^2 3)12x^2-12xy+3y^2 4)8x^3-8x^2y+2xy^2 5)20x^4y^2-20x^3y^3+5x^2y^4
1) \(4x^5y^2-8x^4y^2+4x^3y^2\)
\(=4x^3y^2\left(x^2-2x+1\right)\)
\(=4x^3y^2\left(x^2-2\cdot x\cdot1+1^2\right)\)
\(=4x^3y^2\left(x-1\right)^2\)
2) \(5x^4y^2-10x^3y^2+5x^2y^2\)
\(=5x^2y^2\left(x^2-2x+1\right)\)
\(=5x^2y^2\left(x^2-2\cdot x\cdot1+1^2\right)\)
\(=5x^2y^2\left(x-1\right)^2\)
3) \(12x^2-12xy+3y^2\)
\(=3\left(4x^2-4xy+y^2\right)\)
\(=3\left[\left(2x\right)^2-2\cdot2x\cdot y+y^2\right]\)
\(=3\left(2x-y\right)^2\)
4) \(8x^3-8x^2y+2xy^2\)
\(=2x\left(4x^2-4xy+y^2\right)\)
\(=2x\left[\left(2x\right)^2-2\cdot2x\cdot y+y^2\right]\)
\(=2x\left(2x-y\right)^2\)
5) \(20x^4y^2-20x^3y^3+5x^2y^4\)
\(=5x^2y^2\left(4x^2-4xy+y^2\right)\)
\(=5x^2y^2\left[\left(2x\right)^2-2\cdot2x\cdot y+y^2\right]\)
\(=5x^2y^2\left(2x-y\right)^2\)
1: 4x^5y^2-8x^4y^2+4x^3y^2
=4x^3y^2(x^2-2x+1)
=4x^3y^2(x-1)^2
2: \(=5x^2y^2\left(x^2-2x+1\right)=5x^2y^2\left(x-1\right)^2\)
3: \(=3\left(4x^2-4xy+y^2\right)=3\left(2x-y\right)^2\)
4: \(=2x\left(4x^2-4xy+y^2\right)=2x\left(2x-y\right)^2\)
5: \(=5x^2y^2\left(4x^2-4xy+y^2\right)=5x^2y^2\left(2x-y\right)^2\)
Cho đa thức:
Q=23x^3y^3+17x^3y^3-50x^3y^3+(-2xy)^3
Tính giá trị của Q tại |x-1|=1 và y=-1/2
các anh chị giúp e với
\(Q=23x^3y^3+17x^3y^3-50x^3y^3+(-2xy)^3\)
\(Q=23x^3y^3+17x^3y^3-50x^3y^3+(-8)x^3y^3\)
\(Q=(23+17-50-8)x^3y^3\)
\(Q=-18x^3y^3\)
---
\(|x-1|=1\)
\(TH1:\) \(x-1=1\)
⇒ \(x=1+1=2\)
\(TH2: x-1=-1\)
⇒ \(x=(-1)+1=0\)
---
Tính giá trị của \(Q\) tại \(|x-1|=1\) và \(y=\dfrac{-1}{2}\)
\(TH1: x=2; y=\dfrac{-1}{2}\)
\(Q=-18.2^3.(\dfrac{-1}{2})^3\)
\(Q=-18.8.(\dfrac{-1}{8})^3\)
\(Q=36\)
\(TH1: x=0; y=\dfrac{-1}{2}\)
\(Q=-18.0^3.(\dfrac{-1}{2})^3\)
\(Q=0\)
Vậy \(Q\) ∈ {\({36;0}\)}
Ta có: \(Q=23x^2y^3+17x^3y^3-50x^3y^3+\left(-2xy\right)^3\)
\(=-10x^3y^3-8x^3y^3\)
\(=-18x^3y^3\)
Ta có: |x-1|=1
\(\Leftrightarrow\left[{}\begin{matrix}x-1=1\\x-1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\)
Thay x=2 và y=-1/2 vào Q, ta được:
\(Q=-18\cdot2^3\cdot\left(-\dfrac{1}{2}\right)^3=-18\cdot8\cdot\dfrac{-1}{8}=18\)
Thay x=0 và y=-1/2 vào Q, ta được:
\(Q=-18\cdot0^3\cdot\left(-\dfrac{1}{2}\right)^3=0\)
Cho hệ phương trình 1 3 x − y = 2 3 x + 3 y = 2 . Nghiệm của hệ phương trình là?
A. (x; y) = (0; −2)
B. (x; y) = (0; 2)
C. (x; y) = (−2; 0)
D. (x; y) = (2; 0)
Ta có
1 3 x − y = 2 3 x + 3 y = 2 ⇔ y = 1 3 x − 2 3 x + 3 1 3 x − 2 3 = 2 ⇔ y = 1 3 x − 2 3 x + x − 2 = 2 ⇔ y = 1 3 x − 2 3 x = 2 ⇔ x = 2 y = 0
Vậy hệ phương trình có nghiệm duy nhất (x; y) = (2; 0)
Đáp án: D