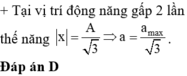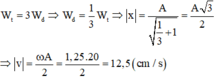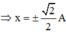Một dao động điều hòa theo pt x=2cos(10t)cm. Vận tốc tại vị trí động năng nhỏ hơn thế năng 3 lần là

Những câu hỏi liên quan
Câu 1: Một chất điểm có khối lượng 200g dao động điều hòa quanh vị trí cân bằng O, phương trình ly độ có dạng x 2cos(10t) (cm), t tính theo đơn vị giây. Lấy gốc thế năng tại O. Tìm biểu thức động năng của chất điểmCâu 2: Một chất điểm có khối lượng 100g dao động điều hòa qunah vị trí cân bằng O, phương trình ly độ có dạng x 6cos(10t) (cm), t tính theo đơn vị giây. Lấy gốc thế năng tại O. Tìm biểu thức thế năng của chất điểm
Đọc tiếp
Câu 1: Một chất điểm có khối lượng 200g dao động điều hòa quanh vị trí cân bằng O, phương trình ly độ có dạng x= 2cos(10t) (cm), t tính theo đơn vị giây. Lấy gốc thế năng tại O. Tìm biểu thức động năng của chất điểm
Câu 2: Một chất điểm có khối lượng 100g dao động điều hòa qunah vị trí cân bằng O, phương trình ly độ có dạng x= 6cos(10t) (cm), t tính theo đơn vị giây. Lấy gốc thế năng tại O. Tìm biểu thức thế năng của chất điểm
Bai 1:
\(\omega=\sqrt{\dfrac{k}{m}}\Rightarrow m=\dfrac{k}{\omega^2};v=x'=-\omega A\sin\left(\omega t+\varphi\right)\)
\(W_d=\dfrac{1}{2}mv^2=\dfrac{1}{2}\dfrac{k}{\omega^2}.\omega^2A^2.\sin^2\left(\omega t+\varphi\right)=\dfrac{1}{4}kA^2\left[1-\cos\left(2\omega t+2\varphi\right)\right]\)
\(\Rightarrow W_d=\dfrac{1}{4}.\omega^2.m.A^2\left[1-\cos\left(2\omega t+2\varphi\right)\right]=\dfrac{1}{4}.100.0,2.4\left[1-\cos\left(20t\right)\right]=20\left[1-\cos\left(20t\right)\right]\)
Bai 2:
\(W_t=\dfrac{1}{2}kx^2=m\omega^2A^2.\dfrac{\cos\left(2\omega t+\varphi\right)+1}{4}=\dfrac{1}{4}m\omega^2.A^2\left[1+\cos\left(2\omega t+2\varphi\right)\right]\)
\(\Rightarrow W_t=\dfrac{1}{4}.0,1.100.36.\left[1+\cos\left(2.10t\right)\right]=90.\left[1+\cos20t\right]\)
Đúng 1
Bình luận (0)
Một vật dao động điều hòa, tại vị trí động năng gấp 2 lần thế năng, gia tốc của vật nhỏ hơn gia tốc cực đại
A. 2 lần.
B. 2 lần.
C. 3 lần.
D. 3 lần.
Một vật dao động điều hòa, tại vị trí động năng gấp 2 lần thế năng, gia tốc của vật nhỏ hơn gia tốc cực đại A. 2 lần B.
2
lần C. 3 lần D.
3
lần
Đọc tiếp
Một vật dao động điều hòa, tại vị trí động năng gấp 2 lần thế năng, gia tốc của vật nhỏ hơn gia tốc cực đại
A. 2 lần
B. 2 lần
C. 3 lần
D. 3 lần
Đáp án D
Tại vị trí động năng gấp 2 lần thế năng
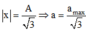
Đúng 0
Bình luận (0)
Một con lắc lò xo dao động điều hòa với vận tốc có độ lớn cực đại bằng 0,4 m/s. Chọn gốc tọa độ tại vị trí cân bằng, gốc thời gian là lúc vật đi qua vị trí x2 cm theo chiều dương và tại đó động năng bằng ba lần thế năng. Phương tình dao động của vật là: A.
x
4
2
cos
10
t...
Đọc tiếp
Một con lắc lò xo dao động điều hòa với vận tốc có độ lớn cực đại bằng 0,4 m/s. Chọn gốc tọa độ tại vị trí cân bằng, gốc thời gian là lúc vật đi qua vị trí x=2 cm theo chiều dương và tại đó động năng bằng ba lần thế năng. Phương tình dao động của vật là:
A. x = 4 2 cos 10 t + π 3 cm
B. x = 4 cos 10 t - π 3 cm
C. x = 4 cos 10 t + π 6 cm
D. x = 4 2 cos 10 t + π 6 cm
Đáp án B
Vận tốc có độ lớn cực đại là 0,4m/s nên ![]()
Lúc vật đang ở vị trí x=2(cm) theo chiều dương thì tại đó động năng bằng ba lần thế năng nên:
W đ = 3 W t ⇒ 4 W t = W ⇒ 4 kx 2 2 = kA 2 2 ⇒ A = 2 x = 4 cm .
Gốc thời gian tại lúc này nên
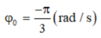
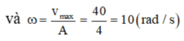
Vậy phương trình dao động của vật là:
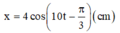
Đúng 0
Bình luận (0)
Một vật dao động điều hoà với phương trình: x1,25cos(20t+
π
2
)cm. Vận tốc tại vị trí mà thế năng gấp 3 lần động năng là A. 12,5 cm/s. B. 10 m/s. C. 7,5 m/s. D. 25 cm/s.
Đọc tiếp
Một vật dao động điều hoà với phương trình: x=1,25cos(20t+ π 2 )cm. Vận tốc tại vị trí mà thế năng gấp 3 lần động năng là
A. 12,5 cm/s.
B. 10 m/s.
C. 7,5 m/s.
D. 25 cm/s.
Một vật nhỏ dao động điều hòa dọc theo trục Ox quanh vị trí cân bằng O. Mốc thế năng tại vị trí cân bằng. Khi vật ở vị trí có li độ x 2 cm, vật có động năng bằng thế năng. Biên độ dao động của vật là A.
2
2
cm B. 4 cm C. 2 cm D.
3
3
cm
Đọc tiếp
Một vật nhỏ dao động điều hòa dọc theo trục Ox quanh vị trí cân bằng O. Mốc thế năng tại vị trí cân bằng. Khi vật ở vị trí có li độ x = 2 cm, vật có động năng bằng thế năng. Biên độ dao động của vật là
A. 2 2 cm
B. 4 cm
C. 2 cm
D. 3 3 cm
một vật dao động điều hòa. tại vị trí động năng băng hai lần thế năng, gia tốc của vật có độ lớn nhỏ hơn gia tốc cực đại mấy lần ?
Một vật dao động điều hòa dọc theo trục Ox, gọi Δt là khoảng thời gian giữa hai lần liên tiếp vật có động năng bằng thế năng. Tại thời điểm t vật qua vị trí có tốc độ 15π
3
cm/s với độ lớn gia tốc 22,5 m/
s
2
, sau đó một khoảng gian đúng bằng t vật qua vị trí có độ lớn vận tốc 45π cm/s. Biên độ dao động của vật là: A. 6
3
cm B. 8cm C. 4
2
cm D. 5...
Đọc tiếp
Một vật dao động điều hòa dọc theo trục Ox, gọi Δt là khoảng thời gian giữa hai lần liên tiếp vật có động năng bằng thế năng. Tại thời điểm t vật qua vị trí có tốc độ 15π 3 cm/s với độ lớn gia tốc 22,5 m/ s 2 , sau đó một khoảng gian đúng bằng t vật qua vị trí có độ lớn vận tốc 45π cm/s. Biên độ dao động của vật là:
A. 6 3 cm
B. 8cm
C. 4 2 cm
D. 5 2 cm
Đáp án A
Δt là khoảng thời gian giữa hai lần liên tiếp vật có động năng bằng thế năng => ∆ t = T 4
Theo đề bài ta có: ![]()
Công thức độc lập với thời gian giữa gia tốc và vận tốc:
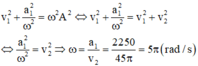
Thay vào công thức tính được biên độ dao động A = 6 3 cm
Đúng 0
Bình luận (0)
Vật nhỏ dao động điều hòa theo phương ngang, mốc thế năng tại vị trí cân bằng. Thế năng bằng 9 lần động năng tại vị trí có li độ x bằng
\(W_t=9\cdot W_đ\Rightarrow W_đ=\dfrac{1}{9}\cdot W_t\)
Để \(W_đ=\dfrac{1}{9}W_t\Rightarrow x=\pm\dfrac{A}{\sqrt{\dfrac{1}{9}+1}}=\pm\dfrac{3\sqrt{10}}{10}A\)
Đúng 0
Bình luận (0)