Cho hình bình hành ABCD ncos phương trình đường chéo AC: x-y+1=0 điểm G(1;4) là trọng tâm tam giác ABC điểm E(0;-3) thuộc đường cao kẻ từ D của tam giác ACD. Tìm toạ độ các đỉnh của hình bình hành cho S tứ giác AGCD=32 và tung độ yA>0

Những câu hỏi liên quan
trong mặt phẳng tọa độ oxy cho hình bình hành ABCD, biết đường chéo AC và BD lần lượt nằm trên 2 đường thẳng d1: x - 5y + 4 = 0, d2: x + 3y -3=0. Phương trình đường thẳng AB: x-y+9=0. tìm tọa độ điểm C.
Cho hình bình hành ABCD. G là điểm trên đường chéo AC, sao cho AG=1/3 AC.Chứng minh BG đi qua trung điểm AD
Cho hình bình hành ABCD có A(-3;-1) B(2;2) giao điểm 2 đường chéo thuộc đường
thẳng x-6y-3=0 diện tích hình bình hành bằng 26. Tìm tọa độ các đỉnh.
Cho hình bình hành ABCD có diện tích bằng 4. Biết tọa độ A(1;0), B(2;0) và giao điểm I của hai đường chéo AC, BD nằm trên đường thẳng y=x. Hãy tìm tọa độ các đỉnh còn lại của hình bình hành ABCD
Từ giả thiết suy ra khoảng cách giữa 2 đường thẳng song song AB, CD bằng 4.
Từ đó, do A, B thuộc Ox nên C(c;4), D(d;4)
Vì 2 đường chéo AC, BD cắt nhau tại I nằm trên đường thẳng y=x nên ta có hệ :
\(\begin{cases}2x=c+1=d+2\\2x=0+4\end{cases}\)
Từ đó tìm được x=2, c=3, d=2.
Vậy C(3;4), D(2;4)
Đúng 0
Bình luận (2)
trong mặt phẳng oxy cho hình bình hành ABCD biết I(7/2;5/2)là trung điểm của CD ,D(3;3/2) và đường phân giác góc BAC có phương trình là denta: x-y+1=0,Xác định tọa độ điểm B
Áp dụng công thức trung điểm: \(\left\{{}\begin{matrix}x_C=2x_I-x_D=4\\y_C=2y_I-y_D=\dfrac{7}{2}\end{matrix}\right.\) \(\Rightarrow C\left(4;\dfrac{7}{2}\right)\)
Gọi d là đường thẳng qua C và vuông góc \(\Delta\Rightarrow d\) nhận (1;1) là 1 vtpt
Phương trình d:
\(1\left(x-4\right)+1\left(y-\dfrac{7}{2}\right)=0\Leftrightarrow x+y-\dfrac{15}{2}=0\)
Gọi E là giao điểm d và \(\Delta\Rightarrow\) tọa độ E là nghiệm:
\(\left\{{}\begin{matrix}x-y+1=0\\x+y-\dfrac{15}{2}=0\end{matrix}\right.\) \(\Rightarrow E\left(\dfrac{13}{4};\dfrac{17}{4}\right)\)
Gọi F là điểm đối xứng C qua \(\Delta\Rightarrow E\) là trung điểm CF
\(\Rightarrow\left\{{}\begin{matrix}x_F=2x_E-x_C=\dfrac{5}{2}\\y_F=2y_E-y_C=5\end{matrix}\right.\) \(\Rightarrow F\left(\dfrac{5}{2};5\right)\)
Do \(\Delta\) là phân giác BAC \(\Rightarrow F\in\) đường thẳng AB
\(\overrightarrow{CD}=\left(-1;-2\right)\), do AB song song DC nên đường thẳng AB nhận (2;-1) là 1 vtpt
Phương trình AB:
\(2\left(x-\dfrac{5}{2}\right)-1\left(y-5\right)=0\Leftrightarrow2x-y=0\)
Tọa độ A là nghiệm: \(\left\{{}\begin{matrix}x-y+1=0\\2x-y=0\end{matrix}\right.\) \(\Rightarrow A\left(1;2\right)\)
\(\overrightarrow{AB}=\overrightarrow{DC}=-\overrightarrow{CD}=\left(1;2\right)\Rightarrow\left\{{}\begin{matrix}x_B=x_A+1=2\\y_B=y_A+2=4\end{matrix}\right.\)
\(\Rightarrow B\left(2;4\right)\)
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD. Biết I (7/2;5/2) là trung điểm của cạnh CD, D (3;3/2) và đường phân giác góc BAC có phương trình là d: x-y+1=0. Xác định tọa độ đỉnh B.
Bài 4.Cho hình bình hành ABCD , O là giao điểm hai đường chéo. Lấy E thuộc AB, F là giao điểm của EO và CD.
1)Chứng minh tứgiác AECF là hình bình hành
2) Kẻ FH//AC ( H thuộc AD), FG//BD ( G thuộc BC).Chứng minh H đối xứng với G qua Ovà tứgiác EHFG là hình bình hành
Trong (Oxy), cho hình bình hành ABCD có tâm I(1;2) và hai đường thẳng AB, AD lần lượt có phương trình là x + 3y - 6 = 0 và 2x - 5y - 1 = 0. Viết phương trình đường thẳng BC và CD.
Ta có: A là giao điểm của AB và AD. Do đó, tọa độ A là nghiệm của hệ phương trình:
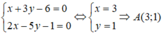
Hình bình hành ABCD có tâm I nên I là trung điểm của AC và BD ⇒ C(-1;3)
Đường thẳng BC đi qua C và song song với AD
Vì BC song song với AD nên BC có dạng: 2x - 5y + c = 0, (c ≠ -1)
Vì C thuộc BC nên: 2.(-1) - 5.3 + c = 0 ⇒ c = 17(tm)
Vậy phương trình đường thẳng BC là: 2x - 5y + 17 = 0
Đường thẳng DC đi qua C và song song với AB
Vì DC song song với AB nên DC có dạng: x + 3y + c = 0, (c ≠ -6)
Vì C thuộc DC nên: -1 + 3.3 + c = 0 ⇒ c = -8(tm)
Vậy phương trình đường thẳng DC là: x + 3y - 8 = 0
Đúng 0
Bình luận (1)
Bài 4.Cho hình bình hành ABCD , O là giao điểm hai đường chéo. Lấy E thuộc AB, F là giao điểm của EO và CD.
1)Chứng minh tứ giác AECF là hình bình hành
2)KẻFH//AC ( H thuộc AD), FG//BD ( G thuộc BC).Chứng minh H đối xứng với G qua Ovà tứgiác EHFG là hình bình hành
Mn giúp mình với mình đang cần gấp ạ















 đđây nhá !
đđây nhá !