1. Không dịch được đề

2.

\(-1\le cos2x\le1\Rightarrow1\le y\le3\)

3.

a. \(-2\le2sinx\le2\Rightarrow-1\le y\le3\)

\(y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)

\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)

b.

\(0\le cos^2x\le1\Rightarrow-1\le y\le2\)

\(y_{min}=-1\) khi \(cos^2x=1\Rightarrow x=k\pi\)

\(y_{max}=2\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)

4.

\(y=\left(tanx-1\right)^2+2\ge2\)

\(y_{min}=2\) khi \(tanx=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)

Đáp án B

Ta có bảng biến thiên

Chọn A

↔ (2-y)sinx + (1+2y)cosx= 3y-1(*)

Sử dụng điều kiện để phương trình (*) có nghiệm suy ra -1/2 ≤ y ≤ 2

Đáp án B

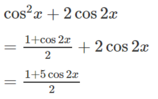
Vì -1 ≤ cos2x ≤ 1 nên giá trị lớn nhất của y là 3, đạt được khi x = 0, giá trị nhỏ nhất của y là -2, đạt được khi x = π/2

Đáp án A.

Điều kiện  x ∈ ℝ

  y = cos x + cos x − π 3 = cos x + cos x . cos π 3 + sin x . sin π 3 = cos x + 1 2 cos x + 3 2 sin x

= 3 2 cos x + 3 2 sin x

Cách 1: y = 3 3 2 cos x + 1 2 sin x = 3 sin x + π 3 Suy ra  − 3 ≤ y ≤ 3

Vậy   m = − 3 ; M = 3 và do đó  M 2 + m 2 = 6

Cách 2:

Áp dụng bất đẳng thức Bunyakovsky ta có:

  3 2 cos x + 3 2 sin x 2 ≤ 3 2 2 + 3 2 2 cos x 2 + sin x 2

  ⇔ 3 2 cos x + 3 2 sin x 2 ≤ 3 ⇔ − 3 ≤ y ≤ 3

  ⇒ M = 3 khi   2 3 cos x = 2 3 sin x 3 2 cos x + 3 2 sin x = 3

Tương tự ta có  m = − 3    khi   2 3 cos x = 2 3 sin x 3 2 cos x + 3 2 sin x = − 3

⇒ M 2 + m 2 = 3 2 + − 3 2 = 6

Vậy ta chọn A.

Đáp án D