Cho hình vuông ABCD,gọi E,F lần lượt là trung điểm của BC,CD ; H là giao của AE,BF. . TínhAH/AE , BH/BF

Những câu hỏi liên quan
a, cho hình thanh ABCD(AB//CD). Gọi E,F lần lượt là trung điểm AD Và BC.
Biết AB=8cm: CD=12cm. Tính độ dài EF.
b, Cho hình thang ABCD(AB//CD). Gọi E,F lần lượt là trung điểm AD và BC.
Biết AB=10cm: EF=16cm. Tính độ dài CD.
Cho hình vuông ABCD tâm I. gọi E, F, G, H lần lượt là trung điểm của các cạnh DA, AB, BC, CD. Phép đối xứng trục AC biến:
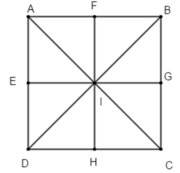
A. ∆IED thành ∆IGC
B. ∆IFB thành ∆IGB
C. ∆IBG thành ∆IDH
D. ∆IGC thành ∆IFA
Tìm ảnh của từng điểm qua phép đối xứng trục AC: điểm I biến thành I; B thành D; G thành H.
Chọn đáp án C
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có AC=BD và AC vuông góc BD. Gọi E, F, G, H lần lượt là trung điểm AB, BC, CD, DA. CMR EFGH là hình vuông
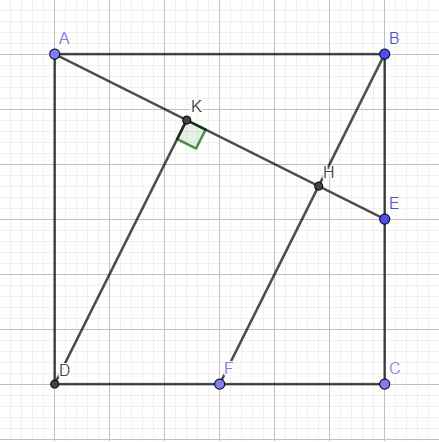
Cho hình vuông ABCD,gọi E,F lần lượt là trung điểm của BC,CD ; H là giao của AE,BF. K là hình chiếu của D lên AH. CMR
a) AE vuông góc BF
b) Tính \(\dfrac{AH}{AE},\dfrac{BH}{BF}\)
c) K là trung điểm AH
a. Dễ dàng chứng minh hai tam giác vuông ABE và BCF bằng nhau (c.g.c)
\(\Rightarrow\widehat{AEB}=\widehat{BFC}\)
Mà \(\widehat{AEB}+\widehat{AEC}=180^0\Rightarrow\widehat{BFC}+\widehat{AEC}=180^0\)
\(\Rightarrow\widehat{EHF}=360^0-\left(\widehat{C}+\widehat{BFC}+\widehat{AED}\right)=90^0\)
Hay \(AE\perp BF\)
b.
Áp dụng hệ thức lượng cho tam giác vuông ABE:
\(AB^2=AH.AE\Rightarrow AH=\dfrac{AB^2}{AE}\Rightarrow\dfrac{AH}{AE}=\dfrac{AB^2}{AE^2}=\dfrac{AB^2}{AB^2+BE^2}=\dfrac{AB^2}{AB^2+\left(\dfrac{AB}{2}\right)^2}=\dfrac{4}{5}\)
\(\dfrac{BH}{BF}=\dfrac{BH}{AE}=\dfrac{\dfrac{AB.BE}{AE}}{AE}=\dfrac{AB.BE}{AE^2}=\dfrac{AB.\dfrac{1}{2}AB}{AB^2+\left(\dfrac{1}{2}AB\right)^2}=\dfrac{2}{5}\)
c. Hai tam giác vuông ABH và DAK đồng dạng (\(\widehat{ADK}\) và \(\widehat{BAH}\) cùng phụ \(\widehat{DAK}\))
\(\Rightarrow\dfrac{AK}{AD}=\dfrac{BH}{AB}\Rightarrow AK=\dfrac{AD.BH}{AB}=BH\)
Mà \(tan\widehat{BAH}=\dfrac{BH}{AH}=\dfrac{BE}{AB}=\dfrac{1}{2}\Rightarrow BH=\dfrac{1}{2}AH\)
\(\Rightarrow AK=\dfrac{1}{2}AH\) hay K là trung điểm AH
Đúng 1
Bình luận (0)
vẽ hình thang ABCD (AB<CD, AD vuông góc BC. Gọi F,E lần lượt là trung điểm của AB và CD chứng minh rằng = 1/2(CD-AB)
Xem thêm câu trả lời
cho hình thang ABCD vuông tại A và D có CD = 2AD = 2AB. gọi E và F lần lượt là trung điểm của AB và BC . CM tam giác DÈ là tam giác vuông cân
Cho hình thang ABCD (AB//CD). Gọi E, F, K lần lượt là trung điểm của BD, AC, DC. Gọi H là giao điểm của đường thẳng E đi qua E vuông góc với AD và đường thẳng F vuông góc với BC. Chứng minh a)H là trực tâm tam giác EFK b) Tam giác HCD cân
cho hcn ABCD. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA
a,CMR EFGH là hình thoi
b,Gọi M, N, P, Q lần lượt là trung điểm EF, FG, GH, HE. CMR MNPQ là hình chữ nhật
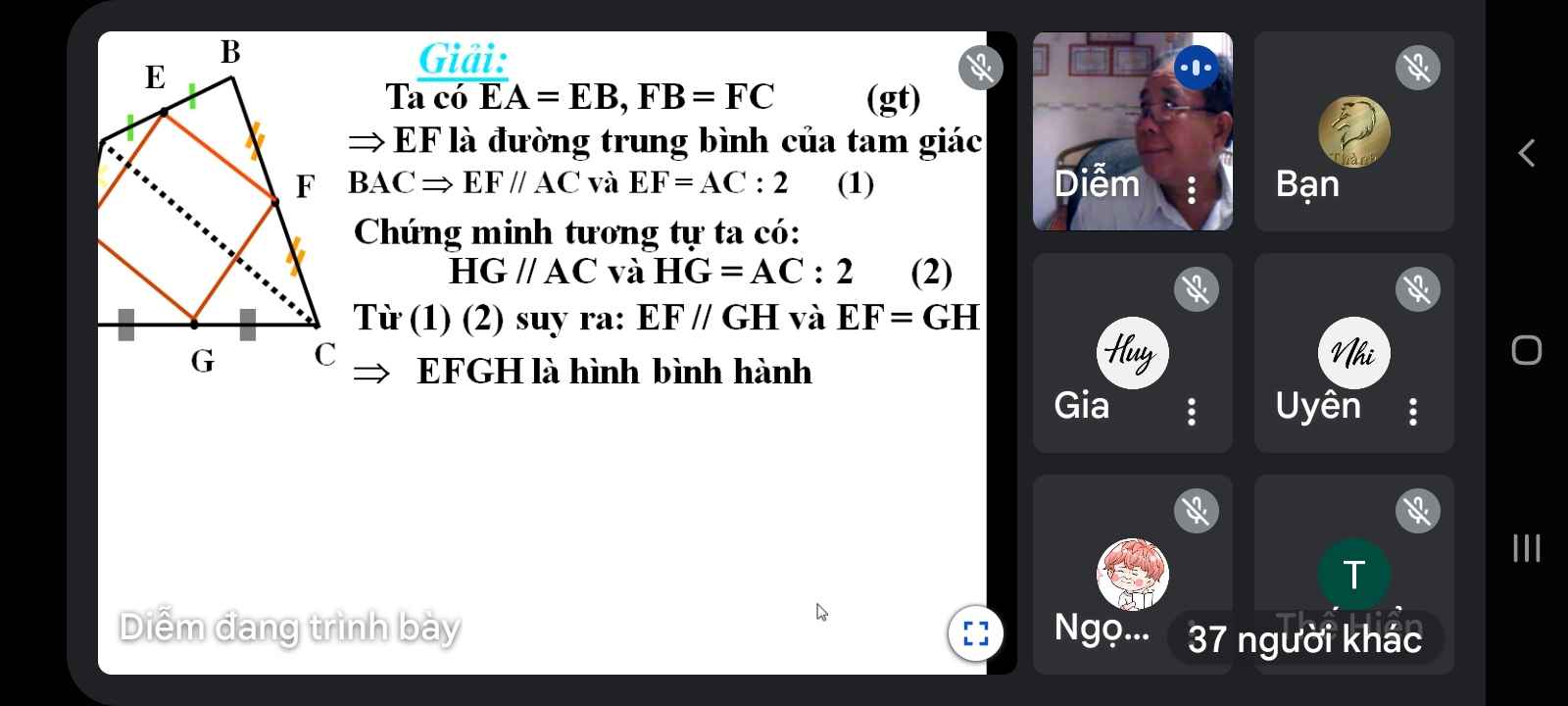
a: Xét ΔBAC có E,F lần lượt là trung điểm của BA,BC
=>EF là đường trung bình
=>EF//AC và EF=AC/2
Xét ΔDAC có
H,G lần lượt là trung điểm của DA,DC
=>HG là đường trung bình
=>HG//AC và HG=AC/2
=>EF//HG và EF=HG
Xét ΔABD có
E,H lần lượt là trung điểm của AB,AD
=>EH là đường trung bình
=>EH=BD/2
=>EH=AC/2=EF
Xét tứ giác EHGF có
EF//GH
EF=GH
EH=EF
Do đó: EHGF là hình thoi
b: Xét ΔEHF có Q,M lần lượt là trung điểm của EH,EF
=>QM là đường trung bình
=>QM//HF và QM=HF/2
Xét ΔGHF có
P,N lần lượt là trung điểm của GH,GF
=>PN là đường trung bình
=>PN//HF và PN=HF/2
=>QM//PN và QM=PN
Xét ΔHEG có HQ/HE=HP/HQ=1/2
nên PQ//EG
=>PQ vuông góc HF
=>PQ vuông góc QM
Xét tứ giác MNPQ có
MQ//NP
MQ=NP
góc PQM=90 độ
Do đó: MNPQ là hình chữ nhật
Đúng 0
Bình luận (0)
cho tứ giác ABCD có AC vuông góc BD . gọi E , F , G , H lần lượt là trung điểm của các cacnhj AB, BC, CD, DA. hỏi tứ giác EFGH là hình gì?Chứng minh