Cho tam giác ABC vuông tại A biết AB=6cm,BC=10cm. Tính SinB+CosB/TanC+CotC

Những câu hỏi liên quan
Cho \(\Delta ABC\) vuông tại A, AB= 6, BC = 10 . Tính \(A=\dfrac{SinB+CosB}{TanC+CotC}\)
\(AC=\sqrt{BC^2-AB^2}=8\\ \Rightarrow A=\dfrac{\dfrac{AC}{BC}+\dfrac{AB}{BC}}{\dfrac{AB}{AC}+\dfrac{AC}{AB}}=\dfrac{\dfrac{AB+AC}{BC}}{\dfrac{6}{8}+\dfrac{8}{6}}=\dfrac{\dfrac{14}{10}}{\dfrac{25}{12}}=\dfrac{7}{5}\cdot\dfrac{12}{25}=\dfrac{84}{125}\)
Đúng 1
Bình luận (0)
: Tam giác ABC vuông tại A. Khẳng định nào sau đây đúng?
A. sinB = sinC B. cosB = cosC C. tanB = cotC D. cotB = cotC
Cho tam giác ABC vuông tại A, đường cao AH ( H thuộc BC ), AB = 6cm, BC = 10cm. a) Tính AC, cosB b) Tính số đo góc BÂH.
a) Áp dụng định lý Pytago:
\(BC^2=AB^2+AC^2\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{10^2-6^2}=8\left(cm\right)\)
Áp dụng tslg:
\(cosB=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
b) Áp dụng HTL :
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow AH=\sqrt{\dfrac{1}{\dfrac{1}{AB^2}}+\dfrac{1}{\dfrac{1}{AC^2}}}=\sqrt{\dfrac{1}{\dfrac{1}{6^2}+\dfrac{1}{8^2}}}=4,8\left(cm\right)\)
Áp dụng tslg:
\(cosBAH=\dfrac{AH}{AB}=\dfrac{4,8}{6}\Rightarrow\widehat{BAH}\approx37^0\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. BIết BH=4cm, CH=9cm:
a/ Tính AB,AC,AH
b/ Cmr: 9.sinB+6.cosB-3.tanC=3√13 -2
c/ Gọi M,N lần lượt là hình chiếu của H trên AB,AC.
Cmr: AM.AN.BC=AH3
Cảm ơn nhiều nếu mn có câu trả lời!
a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=HB\cdot HC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\sqrt{13}\left(cm\right)\\AC=3\sqrt{13}\left(cm\right)\\AH=6\left(cm\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
a)Cho tam giác ABC vuông tại A, biết AB=4cm; BC=5cm, Tonhs cosC+TanB
b) Cho tam giác ABC vuông tại A, có AB=5cm,BC=10cm. Tính sinC và số đo góc B
c) Cho tam giác ABC vuông tại A, biết cosB=8cm. hãy tính các tỉ số lượng giác của góc C. E c.ơn ạ!
Câu a) với b) tính cos, tan, sin là tính góc hay cạnh vậy cậu?
Đúng 0
Bình luận (9)
a) Xét \(\Delta ABC\) vuông tại `A`
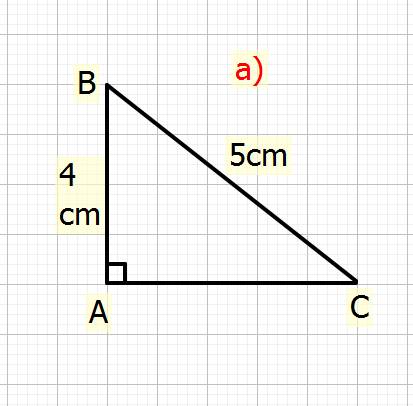
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow5^2=4^2+AC^2\\ \Rightarrow AC^2=5^2-4^2\\ \Rightarrow AC^2=25-16=9\\ \Rightarrow AC=\sqrt{9}=3cm\)
Vậy: \(AC=3cm\)
Ta có: \(CosC=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow CosC=\dfrac{3}{5}\\ \Rightarrow CosC\approx53^o\)
Vậy: Góc C khoảng \(53^o\)
Ta có: \(TanB=\dfrac{AC}{AB}\left(tslg\right)\)
\(\Rightarrow TanB=\dfrac{3}{4}\\ \Rightarrow TanB\approx37^o\)
Vậy: Góc B khoảng \(37^o\)
_
b) Xét \(\Delta ABC\) vuông tại `A`
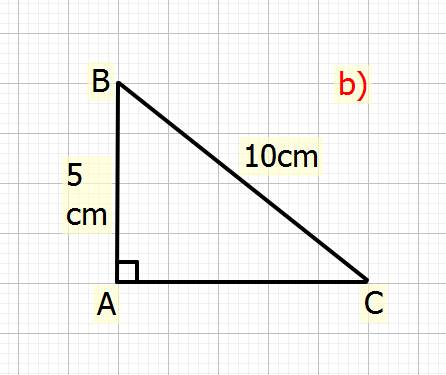
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow10^2=5^2+AC^2\\ \Rightarrow AC^2=10^2-5^2\\\Rightarrow AC^2=100-25=75\\ \Rightarrow AC=\sqrt{75}=5\sqrt{3}cm\)
Vậy: \(AC=5\sqrt{3}cm\)
Ta có: \(SinC=\dfrac{AB}{BC}\left(tslg\right)\)
\(\Rightarrow SinC=\dfrac{5}{10}\\ \Rightarrow30^o\)
Vậy: Góc C là \(30^o\)
Ta có: \(SinB=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow SinB=\dfrac{5\sqrt{3}}{10}\\ \Rightarrow SinB=60^o\)
Vậy: Góc B là \(60^o\).
Đúng 1
Bình luận (2)
Cho ∆ABC vuông tại A, biết AB=6cm,AC=8cm.tính sinB+tanC
Theo định lý Pytago ta tính được BC = 10cm
Vì tam giác ABC vuông tại A nên ta có:
+) sinB = \(\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\)
+) tanC = \(\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\)
=> sinB + tanC= \(\dfrac{4}{5}+\dfrac{3}{4}=\dfrac{31}{20}\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A , AH là đường cao . Biết BH = 2cm ,HC=6cm
a) tính độ dài AH, AB
b) tính sinB,tanC
c) gọi M là điểm bất kỳ trên cạnh AC ( M ≠ A , M ≠ C ) Hạ AI vuôg góc BM ( I ∈ BM ). Chưng minh tam giác BIC ~ tam giác
a/
Xét tg vuông ABC
\(AH^2=BH.HC\) (Trong tg vuông bình phương đường đường cao hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích giữa 2 hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow AH=\sqrt{2.6}=2\sqrt{3}\)
\(BC=BH+HC=2+6=8\)
\(AB^2=BH.BC\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow AB=\sqrt{2.8}=4\)
b/
Xét tg vuông ABH
\(\sin B=\dfrac{AH}{AB}=\dfrac{2\sqrt{3}}{4}=\dfrac{\sqrt{3}}{2}\)
Xét tg vuông ACH
\(\tan C=\dfrac{AH}{HC}=\dfrac{2\sqrt{3}}{6}=\dfrac{\sqrt{3}}{3}\)
c/
Đúng 0
Bình luận (0)
a) \(AH^2=HB.HC=2.6=12\Rightarrow AH=2\sqrt[]{3}\left(cm\right)\)
\(AB^2=AH^2+BH^2=12+4=16\Rightarrow AB=4\left(cm\right)\left(Pitago\right)\)
b) \(SinB=\dfrac{AH}{AB}=\dfrac{2\sqrt[]{3}}{4}=\dfrac{\sqrt[]{3}}{2}\)
\(tanC=\dfrac{AH}{HC}=\dfrac{2\sqrt[]{3}}{6}=\dfrac{\sqrt[]{3}}{3}\)
Câu C bạn xem lại đề
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A,AB=20cm,BC=25cm.Tính
a) Tỉ số lượng giác của góc B
b)P=2 cosB- 3 tanC
Xét tam giác ABC vuông tại A có:
\(BC^2=AB^2+AC^2\left(Pytago\right)\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{25^2-20^2}=15\left(cm\right)\)
a) Áp dụng tslg trong tam giác ABC vuông tại A:
\(\left\{{}\begin{matrix}sinB=\dfrac{AC}{BC}=\dfrac{15}{25}=\dfrac{3}{5}\\cosB=\dfrac{AB}{BC}=\dfrac{20}{25}=\dfrac{4}{5}\\tanB=\dfrac{AC}{AB}=\dfrac{15}{20}=\dfrac{3}{4}\\cotB=\dfrac{AB}{AC}=\dfrac{20}{15}=\dfrac{4}{3}\end{matrix}\right.\)
b) Ta có: \(tanC=\dfrac{AB}{AC}=\dfrac{20}{15}=\dfrac{4}{3}\)
\(P=2cosB-3tanC=2.\dfrac{4}{5}-3.\dfrac{4}{3}=-\dfrac{12}{5}\)
Đúng 4
Bình luận (2)
cho tam giác ABC vuông tại A,AB=20cm,BC=25cm.Tính
a) Tỉ số lượng giác của góc B
b)P=2 cosB- 3 tanC























