Cho tứ giác ABCD. Chứng minh rằng: AC + BD > (Chu vi ABCD/2)

Những câu hỏi liên quan
cho tứ giác ABCD . gọi O là giao điểm của hai đường chéo AC và BD . gọi chu vi của tứ giác ABCD là PABCD . chứng minh
a) AC+BD>\(\dfrac{P_{ABCD}}{2}\)
b) Nếu AC<\(\dfrac{P_{ABCD}}{2}\) thì AC+BD<PABCD
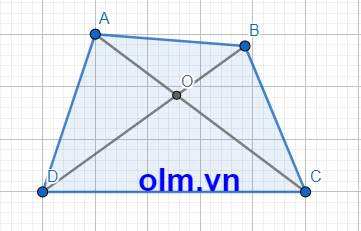
a, Xét \(\Delta\) AOB có: AO+OB > AB (trong tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Tương tự ta có: OC + OD > DC
OA + OD > AD
OB + OC > BC
Cộng vế với vế ta có:
OA+OB+OC+OD+OA+OD+OB+OC > AB +DC+AD+BC
(OA+OC)\(\times\)2 + (OB + OD)\(\times\)2 > PABCD
AC \(\times\) 2 + BD \(\times\) 2 > PABCD
AC + BD > \(\dfrac{P_{ABCD}}{2}\) (đpcm)
b, Xét \(\Delta\) ABD có: AB + AD > BD (trong tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại)
Tương tự ta có: AD + DC > AC
DC + CB > DB
CB + AB > AC
Cộng vế với vế ta có:
AB+AD+AD+DC+DC+CB+CB+AB >BD+ AC+DB+AC
2AB+2BC+2CD+2AD> 2AC + 2BD
2(AB + BC + CD + AD) > 2(AC + BD)
AB + BC + CD + AD > AC + BD
PABCD > AC + BD (đpcm)
Đúng 0
Bình luận (0)
1.Cho tứ giác ABCD. Chứng minh rằng \(\frac{1}{2}\)p< AC + BD< p ( với p là chu vi cùa tứ giác ABCD)
2.Cho tứ giác ABCD, M là một điểm nằm trong tứ giác đó. Xác định vị trí của M để MA+MB+MC+MD nhỏ nhất.
cho tứ giác ABCD . gọi O là giao điểm của hai đường chéo AC và BD . Gọi chu vi tứ giác ABCD là PABCD Chứng minh
a)AC+BD>\(\dfrac{P_{ABCD}}{2}\)
b)Nếu AC<\(\dfrac{P_{ABCD}}{2}\) thì AC+BD<PABCD
cho tứ giác ABCD. Chứng minh rằng:
a) Nếu AC=AD thì BC<BD
b)Nếu chu vi tam giác ADB không lớn hơn chu vi tam giác ACD thì AB<AC
cho tứ giác ABCD Chứng minh rằng :
a) Nếu AC=AD thì BC<BD
b) Nếu chu vi tam giác ABD không lớn hơn chu vi tam giác ACD thì AB<AC
Cho tứ giác ABCD có 2 đuowngf chéo AC,BD cắt nhau tại O tạo thành 4 tam giác OAB,OBC,OCD,ODA có chu vi băfng nhau. Chứng minh tứ giác ABCD là hình thoi
CHO TỨ GIÁC ABCD. CHỨNG MINH RẰNG \(\frac{1}{2}\)p < AC+BD < p (p là chu vi tứ giác)
CÁC BẠN GIẢI GIÙM MÌNH
XIN CẢM ƠN !!!!!
AC BD của tứ giác ABCD cắt tại O.Cho chu vi các tam giác AOB BOC COD DOA có chu vi bằng nhau chứng minh ABCD là hình thoi
1/ cho tứ giác lồi ABCD có B+D180 độ, CBCD. CMR AC là tia p/giác của góc BAD2/ cho tứ giác lồi ABCD, hai cạnh AD và BC cắt nhau tại E, hai cạnh DC và AB cắt nhau tại F. Kẻ 2 p/giác của 2 góc CED và BFC cắt nhau tại I. Tính góc EIF theo các góc trong của tứ giác ABCD3/ Cho tứ giác ABCD.a) CMR 1/2 p AC+BD p (p là chu vi tứ giác)b) C/M AB+CD AC+BDc) Biết chu vi tam giác ABD nhỏ hơn chu vi tam giác ACD, chứng minh ABAC.
Đọc tiếp
1/ cho tứ giác lồi ABCD có B+D=180 độ, CB=CD. CMR AC là tia p/giác của góc BAD
2/ cho tứ giác lồi ABCD, hai cạnh AD và BC cắt nhau tại E, hai cạnh DC và AB cắt nhau tại F. Kẻ 2 p/giác của 2 góc CED và BFC cắt nhau tại I. Tính góc EIF theo các góc trong của tứ giác ABCD
3/ Cho tứ giác ABCD.
a) CMR 1/2 p < AC+BD < p (p là chu vi tứ giác)
b) C/M AB+CD < AC+BD
c) Biết chu vi tam giác ABD nhỏ hơn chu vi tam giác ACD, chứng minh AB<AC.













