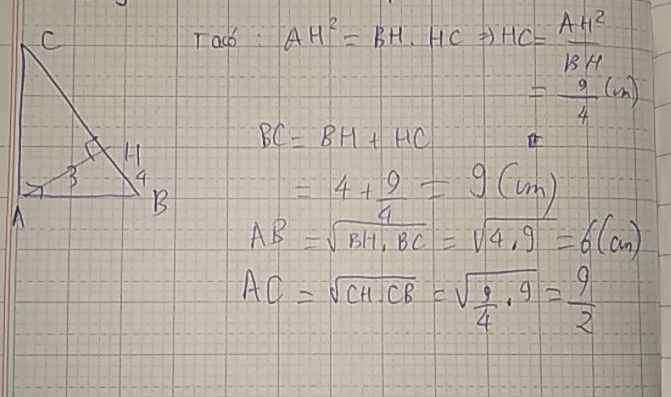Ta có:

\(AH^2=BH.HC\Rightarrow HC=\dfrac{AH^2}{BH}=\dfrac{3^2}{4}=\dfrac{9}{4}\left(cm\right)\)

\(BC=BH+HC=4+\dfrac{9}{4}=9\left(cm\right)\)

\(AB=\sqrt{BH.BC}=\sqrt{4.9}=6\left(cm\right)\)

\(AC=\sqrt{CH.BC}=\sqrt{\dfrac{9}{4}.9}=\dfrac{9}{2}\left(cm\right)\)

\(AH^2=BH.HC\) (trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích hai hình chiếu của 2 cạnh góc vuông trên cạnh huyền)

\(\Rightarrow HC=\dfrac{AH^2}{BH}=\dfrac{3^2}{4}=2,25cm\)

\(BC=BH+HC=4+2,25=6,25cm\)

\(AB^2=BH.BC\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giwac hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)

\(\Rightarrow AB=\sqrt{BH.BC}=\sqrt{4.6,25}=5cm\)

\(AC=\sqrt{BC^2-AB^2}\) (Pitago)

\(\Rightarrow AC=\sqrt{6,25^2-5^2}=3,75cm\)

a: Xet ΔAHB vuông tại H và ΔCHA vuông tại H có

góc HAB=góc HCA

=>ΔAHB đồng dạng với ΔCHA

b: \(BH=\sqrt{15^2-12^2}=9\left(cm\right)\)

HC=12^2/9=16cm

CA=căn 16*25=20cm

c: CF/CA=4/20=1/5

CE/CB=5/25=1/5

=>CF/CA=CE/CB

=>ΔCFE đồng dạng với ΔCAB

=>góc CFE=90 độ

=>ΔCFE vuông tại F

a: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có

góc HAB=góc HCA
=>ΔHAB đồng dạngvới ΔHCA
b: \(BH=\sqrt{15^2-12^2}=9\left(cm\right)\)

BC=15^2/9=25(cm)

\(AC=\sqrt{25^2-15^2}=20\left(cm\right)\)

c: CE/CB=CF/CA

góc C chung

=>ΔCEF đồng dạng với ΔCBA

=>góc CFE=góc CAB=90 độ

=>ΔCEF vuông tại F

d: CE/CB=CF/CA

=>CE*CA=CF*CB

a, Xét tam giác ABH và tam giác CAH ta có : 

^AHB = ^CHA = 90⁰

^BAH = ^HCA ( cùng phụ ^HAC )

Vậy tam giác ABH ~ tam giác CAH ( g.g )

b, Xét tam giác ABC vuông tại A, đường cao AH

Áp dụng định lí Pytago cho tam giác AHB vuông tại H 

\(AB^2=BH^2+AH^2\Rightarrow BH^2=AB^2-AH^2=225-144=81\Rightarrow BH=9\)cm 

* Áp dụng hệ thức : 

\(AH^2=BH.HC\Rightarrow HC=\dfrac{AH^2}{BH}=\dfrac{144}{9}=16\)cm 

=> BC = HC + HB = 16 + 9 = 25 cm 

* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AC=\dfrac{AH.BC}{AB}=\dfrac{12.25}{15}=20\)cm

a) Xét ΔBHA vuông tại H và ΔAHC vuông tại H có 

\(\widehat{BAH}=\widehat{ACH}\left(=90^0-\widehat{B}\right)\)

Do đó: ΔBHA\(\sim\)ΔAHC(g-g)

Xét ΔABC vuông tại A có AH là đường cao

nên \(AB^2=BH\cdot BC\)

=>\(BC\cdot2,5=6,5^2\)

=>\(BC=\dfrac{6.5^2}{2.5}=16,9\left(cm\right)\)

ΔAHB vuông tại H

=>\(HA^2+HB^2=AB^2\)

=>\(HA=\sqrt{6.5^2-2.5^2}=6\left(cm\right)\)

HC+HB=BC

=>HC+2,5=16,9

=>HC=14,4(cm)

ΔAHC vuông tại H

=>\(HA^2+HC^2=AC^2\)

=>\(AC^2=14,4^2+6^2=243,86\)

=>AC=15,6(cm)

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC^2=6^2+8^2=100\)

=>BC=10(cm)

Xét ΔABC vuông tại A có AH là đường cao

nên AH*BC=AB*AC

=>AH*10=6*8=48

=>AH=4,8(cm)

ΔABC vuông tại A có AH là đường cao

nên \(\left\{{}\begin{matrix}BH\cdot BC=BA^2\\CH\cdot CB=CA^2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}BH=\dfrac{6^2}{10}=3,6\left(cm\right)\\CH=\dfrac{8^2}{10}=6,4\left(cm\right)\end{matrix}\right.\)

a) Sửa đề: C/m tam giác AHB đồng dạng với tam giác CHA

Xét ΔAHB vuông tại H và ΔCHA vuông tại H có 

\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)

Do đó: ΔAHB∼ΔCHA(g-g)