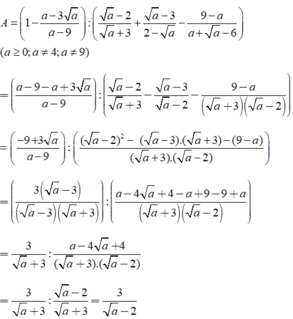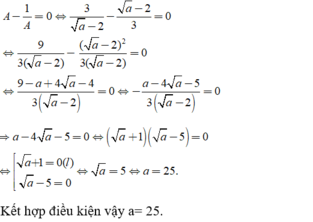chứng minh a=-3,5 giá trị biểu thức A=(a+3) (9a-8)-(2a+a) (9a-1) bằng -29

Những câu hỏi liên quan
chung minh rằng với a=-3,5 giá trị của biểu thức
A =(a+3)9a-8) - (2+a)(9a-1) bằng -29
chắc đề thế này @@ (a+3)(9a-8) - (2+a)(9a-1)
=9a2-8a+27a-24-9a2-17a+2
=(9a2-9a2)+(-8a+27a-17a)-24+2
=2a-22.Thay a=-3,5 vào được:2*(-3,5)-22
=-7-22=-29.Đpcm
Đúng 0
Bình luận (0)
Câu 1: CMR: với a=3,5 gt đa thức:
A= (a+3)(9a-8) . (2+a)(9a-1)=-29
Cho biểu thức
A
1
-
a
-
3
a
a
-
9
a
-
2
a
+
3...
Đọc tiếp
Cho biểu thức
A = 1 - a - 3 a a - 9 a - 2 a + 3 + a - 3 2 - a - 9 - a a + a - 6
Tìm giá trị của a để A - 1/A = 0?
A. a = 5
B. a = 3
C. a = 36
D. a = 25
giúp mình với ạ:
Bài 1:
a) CM: với a = -3 giá trị biểu thức A = (a+3)(9a-8) - (2+a)(9a-1) bằng -28
b) CM rằng biểu thức sau không phụ thuộc vào x: Q = (3x-5)(2x+11) - (2x+3)(3x+7)
a: \(A=\left(a+3\right)\left(9a-8\right)-\left(a+2\right)\left(9a-1\right)\)
\(=9a^2-8a+27a-24-\left(9a^2-a+18a-2\right)\)
\(=9a^2+19a-24-9a^2-17a+2=2a-22\)
Thay a=-3 vào A, ta được:
\(A=2\cdot\left(-3\right)-22=-6-22=-28\)
b: \(Q=\left(3x-5\right)\left(2x+11\right)-\left(2x+3\right)\left(3x+7\right)\)
\(=6x^2+33x-10x-55-\left(6x^2+14x+9x+21\right)\)
\(=6x^2+23x-55-6x^2-23x-21\)
=-55-21
=-76
=>Q không phụ thuộc vào biến x
Đúng 0
Bình luận (0)
Chắc chắn rồi! Mình sẽ giúp bạn giải từng phần của bài toán này.
Bài 1:a) Chứng minh rằng với \(a = - 3\), giá trị của biểu thức \(A = \left(\right. a + 3 \left.\right) \left(\right. 9 a - 8 \left.\right) - \left(\right. 2 + a \left.\right) \left(\right. 9 a - 1 \left.\right)\) bằng -28.Biểu thức cần chứng minh:\(A = \left(\right. a + 3 \left.\right) \left(\right. 9 a - 8 \left.\right) - \left(\right. 2 + a \left.\right) \left(\right. 9 a - 1 \left.\right)\)
Thay giá trị \(a = - 3\) vào biểu thức:
\(A = \left(\right. - 3 + 3 \left.\right) \left(\right. 9 \left(\right. - 3 \left.\right) - 8 \left.\right) - \left(\right. 2 + \left(\right. - 3 \left.\right) \left.\right) \left(\right. 9 \left(\right. - 3 \left.\right) - 1 \left.\right)\)Tính các phần trong biểu thức:
\(A = 0 \times \left(\right. 9 \left(\right. - 3 \left.\right) - 8 \left.\right) - \left(\right. 2 - 3 \left.\right) \left(\right. 9 \left(\right. - 3 \left.\right) - 1 \left.\right)\)
Cập nhật lại biểu thức:
\(A = 0 \times \left(\right. - 35 \left.\right) - \left(\right. - 1 \left.\right) \left(\right. - 28 \left.\right)\)Phần 1: \(\left(\right. - 3 + 3 \left.\right) = 0\)Phần 2: \(9 \left(\right. - 3 \left.\right) - 8 = - 27 - 8 = - 35\)Phần 3: \(\left(\right. 2 - 3 \left.\right) = - 1\)Phần 4: \(9 \left(\right. - 3 \left.\right) - 1 = - 27 - 1 = - 28\)Tiếp tục tính toán:
\(A = 0 - \left(\right. - 1 \left.\right) \left(\right. - 28 \left.\right) = 0 - 28 = - 28\)
Vậy, \(A = - 28\), chứng minh được yêu cầu.
b) Chứng minh rằng biểu thức \(Q = \left(\right. 3 x - 5 \left.\right) \left(\right. 2 x + 11 \left.\right) - \left(\right. 2 x + 3 \left.\right) \left(\right. 3 x + 7 \left.\right)\) không phụ thuộc vào \(x\).Để chứng minh biểu thức không phụ thuộc vào \(x\), chúng ta cần rút gọn biểu thức và kiểm tra xem có phần nào chứa \(x\)hay không.
Mở rộng các phần trong biểu thức:\(\left(\right. 3 x - 5 \left.\right) \left(\right. 2 x + 11 \left.\right) = 3 x \left(\right. 2 x + 11 \left.\right) - 5 \left(\right. 2 x + 11 \left.\right)\)\(= 6 x^{2} + 33 x - 10 x - 55\)\(= 6 x^{2} + 23 x - 55\)
Tiếp theo, mở rộng phần thứ hai:
\(\left(\right. 2 x + 3 \left.\right) \left(\right. 3 x + 7 \left.\right) = 2 x \left(\right. 3 x + 7 \left.\right) + 3 \left(\right. 3 x + 7 \left.\right)\)\(= 6 x^{2} + 14 x + 9 x + 21\)\(= 6 x^{2} + 23 x + 21\)Lấy hiệu của hai biểu thức vừa rút gọn:
\(Q = \left(\right. 6 x^{2} + 23 x - 55 \left.\right) - \left(\right. 6 x^{2} + 23 x + 21 \left.\right)\)\(Q = 6 x^{2} + 23 x - 55 - 6 x^{2} - 23 x - 21\)Rút gọn các hạng tử:
\(Q = \left(\right. 6 x^{2} - 6 x^{2} \left.\right) + \left(\right. 23 x - 23 x \left.\right) - 55 - 21\)\(Q = 0 x^{2} + 0 x - 76\)\(Q = - 76\)
Vậy, biểu thức \(Q\) không có phần nào chứa \(x\) và bằng -76, do đó không phụ thuộc vào \(x\).
Kết luận:Phần (a): Đã chứng minh được \(A = - 28\) khi \(a = - 3\).Phần (b): Đã chứng minh được \(Q = - 76\), biểu thức không phụ thuộc vào \(x\).
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Tính giá trị biểu thức: C=2a^2+5a+2/2a^3+9a^2+12a+4 với a=201220122012
Nhanh lên nha, mình cần gấp
Chứng minh:
(a-1)(a-2)(1+a+a^2)(4+2a+a^2)=a^6-9a^3+8
\(VT=\left(a-1\right)\left(a-2\right)\left(1+a+a^2\right)\left(4+2a+a^2\right)\)
\(=\left(a^3-1\right)\left(a^3-8\right)\)
\(=a^6-8a^3-a^3+8\)
\(=a^6-9a^3+8=VP\)
\(\Rightarrowđpcm\)
Đúng 0
Bình luận (0)
Cho biểu thức A = \(\dfrac{\sqrt{x}+2}{\sqrt{x}-3};B=\dfrac{\sqrt{x}+5}{\sqrt{x}+1}+\dfrac{\sqrt{x}-7}{1-x}\) với x ≥ 0;x ≠ 1;x ≠ 9
a, Tính giá trị biểu thức A khi x = 16
b,Chứng minh rằng: B = \(\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\)
c, Tìm các giá trị x để \(\dfrac{4A}{A}\le\dfrac{x}{\sqrt{x}-3}\)
\(a,x=16\Rightarrow A=\dfrac{\sqrt{16}+2}{\sqrt{16}-3}=\dfrac{4+2}{4-3}=6\)
\(b,B=\dfrac{\sqrt{x}+5}{\sqrt{x}+1}+\dfrac{\sqrt{x}-7}{1-x}\left(dk:x\ge0,x\ne1,x\ne9\right)\\ =\dfrac{\sqrt{x}+5}{\sqrt{x}+1}-\dfrac{\sqrt{x}-7}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\left(\sqrt{x}+5\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}-7\right)}{x-1}\\ =\dfrac{x+4\sqrt{x}-5-\sqrt{x}+7}{x-1}\\ =\dfrac{x+3\sqrt{x}+2}{x-1}\\ =\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\left(dpcm\right)\)
\(c,\dfrac{4A}{A}\le\dfrac{x}{\sqrt{x}-3}\Leftrightarrow\dfrac{4\left(\sqrt{x}+2\right)}{\sqrt{x}-3}:\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\le\dfrac{x}{\sqrt{x}-3}\)
\(\Leftrightarrow\dfrac{4\left(\sqrt{x}+2\right)}{\sqrt{x}-3}.\dfrac{\sqrt{x}-3}{\sqrt{x}+2}\le\dfrac{x}{\sqrt{x}-3}\)
\(\Leftrightarrow4-\dfrac{x}{\sqrt{x}-3}\le0\)
\(\Leftrightarrow\dfrac{4\sqrt{x}-12-x}{\sqrt{x}-3}\le0\)
\(\Leftrightarrow\) Pt vô nghiệm
Vậy không có giá trị x thỏa yêu cầu đề bài.
Đúng 2
Bình luận (0)
Chứng minh rằng với a=-3.5 thì giá trị của biểu thức A=(a+3)(9a-8)-(2+a)(9a-1)=-29
pạn chỉ cần thế a=-3.5 vào biểu thức A là ra kết quả ngay
Đúng 0
Bình luận (0)
A=(a+3)(9a-8)-(2+a)(9a-1)=-29
Thay a=3,5 vào biểu thức trên
Ta có = (-3,5+3)(9X-3,5-8)-(2+-3,5)(9X-3,5-1)
= -1/2 X(-79/2) - 3/2 (-65/2)
= 79/4 - 195/4
=-29
Đúng 0
Bình luận (0)
tính giá trị biểu thức (2a-b)/(3a-b)+(5b-a)/(3a+b)-3 biết 10a^2-3b^2-5ab=0 và 9a^2-b^2 khác 0