Cho tam giác ABC, M nằm trên cạnh BC sao cho BM = MC = MA. Chứng minh: Tam giác ABC vuông tại A

Những câu hỏi liên quan
cho tam giác ABC vuông cân tại A. M nằm trong tam giác ABC sao cho : BM=BA và góc ABM=36 độ. chứng minh rằng: MA=MC. ( chứng minh bằng 2 cách)
Cho tam giác ABC vuông tại A, tia phân giác góc B cắt AC tại M. Trên cạnh BC lấy điểm D sao cho AD=AB.
a) Chứng minh tam giác ADM = tam giác DBM
b) Chứng minh MD vuông góc với BC
c) So sánh MC và MA
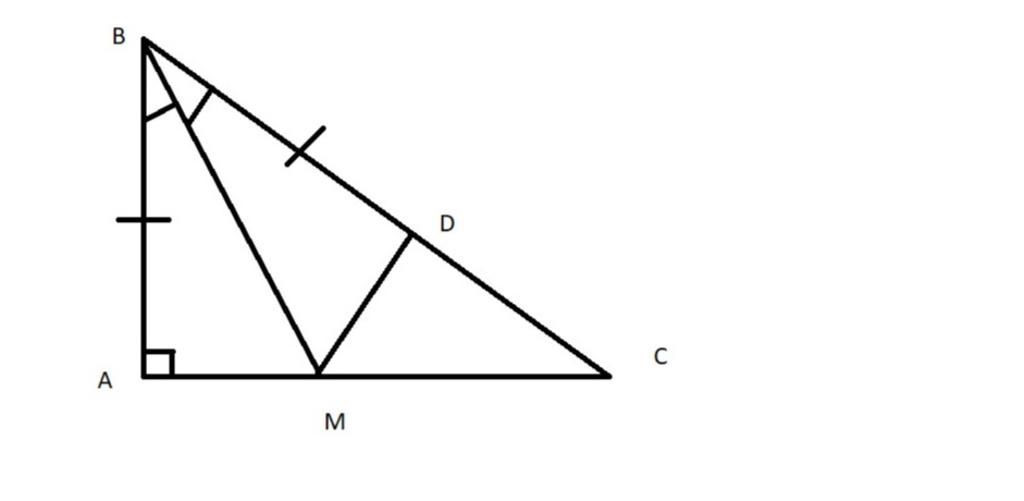

a)Xét △ABM và △△ DBM , ta có :
AB=BD(gt)
ˆABM^ == ˆDBM^ ( vì BM là tia phân giác của ˆABC^ )
BM là chung
⇒ △△ ABM= △△ DBM(c−g−c)
b)Ta có : ˆBAM^ == ˆBDM (( vì △ ABM= △ DBM)
Mà ˆBAM^ =90o(=90) ( vì △ ABC vuông tại A)
⇒⇒ ˆBDM=90o
⇒MD⇒ ⊥⊥ BC
c) Vì MD⊥⊥ BC(cmt)
⇒ ˆMDC^ =90o=90
⇒ △ MDC vuông tại D
⇒MC>MD(ch>cgv)
Mà MD=MA( vì △ABM=△ DBM)
⇒MC>MA
Đúng 0
Bình luận (0)
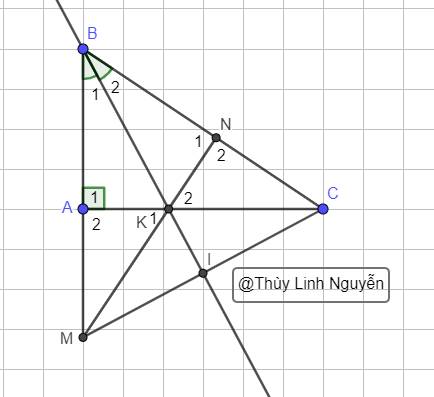
Cho tam giác ABC vuông tại A . Lấy điểm M trên tia BA sao cho BM = BC . Phân giác tam giác ABC cắt AC ở K , cắt MC ở I . Trên cạnh BC lấy điểm N sao cho CN = MA .
C/m: K , M , N thẳng hàngTrước tiên, ta có BM = BC theo đề bài. Vì tam giác ABC vuông tại A, nên ta có góc BAC = 90 độ.
Tiếp theo, ta biết rằng phân giác tam giác ABC cắt AC tại K. Vì vậy, ta có góc BAK = góc CAK.
Tương tự, phân giác tam giác ABC cắt MC tại I, nên ta có góc BAM = góc CAM.
Vì CN = MA, nên ta có góc CAN = góc CMA.
Từ các quan sát trên, ta có thể thấy rằng góc BAK = góc BAM = góc CAN = góc CMA.
Vì vậy, ta có thể kết luận rằng K, M, N thẳng hàng.
Đúng 0
Bình luận (0)
BN+NC=BC
BA+AM=BM
mà BC=BM và NC=AM
nên BN=BA
Xét ΔBAK và ΔBNK có
BA=BN
góc ABK=góc NBK
BK chung
Do đó: ΔBAK=ΔBNK
=>góc BNK=90 độ và KA=KN
Xét ΔKAM vuông tại A và ΔKNC vuông tại N có
KA=KN
AM=NC
Do đó; ΔKAM=ΔKNC
=>góc AKM=góc NKC
=>góc AKM+góc AKN=180 độ
=>K,M,N thẳng hàng
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a tia phân giác của góc b cắt ac tại m trên cạnh bc lấy điểm d sao cho ab=bd a) chứng minh tam giác ABM=DBM b) chứng minh md vuông góc với bc c) so sánh mc và ma
a: Xét ΔABM và ΔDBM có
BA=BD
\(\widehat{ABM}=\widehat{DBM}\)
BM chung
Do đó: ΔABM=ΔDBM
b: Ta có: ΔBAM=ΔBDM
nên \(\widehat{BAM}=\widehat{BDM}=90^0\)
hay MD\(\perp\)BC
c: Ta có: MA=MD
mà MD<MC
nên MA<MC
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A, cạnh đáy < cạnh bên. Trên tia đối của tia BC lấy điểm M sao cho MA = MC. Trên tia đối của AM lấy điểm N sao cho AN = BM. a) Chứng minh góc AMC = BAC; b) Chứng minh CM = CN; c) Tìm điều kiện của TG ABC để CM vuông góc với CN.
Cho tam giác ABC vuông tại A. Lấy điểm M trên tia BA sao cho BM = BC. Phân giác của tam giác ABC cắt AC ở K, cắt MC ở I. Trên cạnh BC lấy điểm N sao cho CN = MA.
Chứng minh K, M, N thẳng hàng.
*lâu r ms lm hình:DD*
+,Có `BK` là p/g `=>hat(B_1)=hat(B_2)`
Có `BM=BC` và `AM=NC` (\(gt\))
`=>BM-AM=BC-NC`
hay `BA=BN`
Xét `Delta ABK` và `Delta NBK` có :
`{:(BK-chung),(hat(B_1)=hat(B_2)(cmt)),(BA=BN(cmt)):}}`
`=>Delta ABK = Delta NBK(c.g.c)`
`=>{(hat(A_1)=hat(N_1)(tương.ứng)(1)),(AK=NK(tương.ứng)):}`
+, Từ `(1)` ; `hat(A_1)+hat(A_2)=180^0` (kề bù) ; `hat(N_1)+hat(N_2)=180^0` (kề bù)
`=>hat(A_2)=hat(N_2)`
Xét `Delta AKM` và `Delta NKC` có :
`{:(AK=NK(cmt)),(hat(A_2)=hat(N_2)(cmt)),(AM=NC(Gt)):}}`
`=>Delta AKM=Delta NKC (c.g.c)`
`=>hat(K_1)=hat(K_2)` ( 2 góc tương ứng )
`=>hat(K_1)+hat(AKN)=hat(K_2)+hat(AKN)`
hay `hat(MKN)=hat(CKA)`
mà `hat(CKA)=180^0` (`K in AC` )
Nên `hat(MKN)=180^0`
`=>M ; K ; N` thẳng hàng
Hình :
Đúng 3
Bình luận (0)
tam giác abc vuông tại a tia phân giác của b cắt ac tại m trên cạnh lấy điểm h sao cho bh bằng ba chứng minh gh vuông góc với bc chứng minh mc chừ ma bé hơn hc
a: Xét ΔBAM và ΔBHM có
BA=BH
góc ABM=góc HBM
BM chung
=>ΔBAM=ΔBHM
=>góc BAM=góc BHM=90 độ
MC-MA=MC-MH<HC
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A (AB<BC) Vẽ AH vuông góc với BC tại H
A) chứng minh tam giác abh bằng tam giác ach và HB = HC
B) Gọi K là trung điểm của AC đường thẳng vuông góc với AC tại K cắt BC tại M chứng minh MA = MC
C) chứng minh góc ABC = góc MAK
D) Trên tia đối của tia ma lấy điểm N sao cho BM = a chứng minh tam giác cmn cân
Ai nhanh mình tick
a) xét tam giác ABH và tam giác ACH có
Góc AHB =Góc AHC =90 độ
AB =AC ( do tam giác abc cân)
Góc B = góc C (do tam giác abc cân)
=> tam giác ABH = tam giác ACH ( cạnh huyền, góc nhọn)
=>HB= HC (hai cạnh tương ứng bằng nhau)
b) Xét tam giác MAK và tam giác MCK có
AK=KH( gì)
Góc AKB = GÓC CKB=90 độ
MK chung
=>tam giác MAK = tam giác MCK( c. g. c)
=> MA=CM( hai cạnh tương ứng)
c) từ tam giác mak = tam giác MCK ( câu b)
=>góc MAK = góc C (..)
TA CÓ tam giác abc cân ở A =>góc B = góc C
=>góc Abc = góc Mak
d) cậu xem lại đề phần này đi nha mik thấy nó sai cái j đó
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, góc ABC = 30độ
a) Tính góc ACB
b) Cho M là trung điểm của cạnh BC. Trên tia đối của MA sao cho MN=MA chứng minh tam giác BMN= tam giác CMN
c) Chứng minh NC=AC
d)Chứng minh AN=BC
a: \(\widehat{ACB}=90^0-30^0=60^0\)
d: Xét tứ giác ABNC có
M là trung điểm của BC
M là trung điểm của AN
Do đó: ABNC là hình bình hành
mà \(\widehat{CAB}=90^0\)
nên ABNC là hình chữ nhật
Suy ra: AN=BC
Đúng 0
Bình luận (0)

















