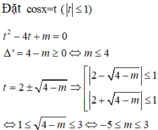điều kiện của tham số m để x^2 -2x+m+3 = 0 có nghiệm

Những câu hỏi liên quan
Tìm điều kiện của tham số m để phương trình
m
x
2
–
2
(
m
–
1
)
x
+
m
−
3
0
có nghiệm A. m
≥
1 B. m 1 C. m
≥
−1 D. m
≤
−1
Đọc tiếp
Tìm điều kiện của tham số m để phương trình m x 2 – 2 ( m – 1 ) x + m − 3 = 0 có nghiệm
A. m ≥ 1
B. m > 1
C. m ≥ −1
D. m ≤ −1
Phương trình mx2 – 2(m – 1)x + m − 3 = 0
(a = m; b = −2(m – 1); c = m – 3)
TH1: m = 0 ta có phương trình
2x – 3 = 0 ⇔ 2x = 3 ⇔ x = 3 2
TH2: m ≠ 0, ta có ∆ = b2 – 4ac = 4 (m – 1)2 – 4m. (m – 3)
= 4m2 – 8m + 4 – 4m2 + 12 = 4m + 4
Để phương trình đã cho có nghiệm thì ∆ ≥ 0
⇔ 4m + 4 ≥ 0 ⇔ 4m ≥ −4 ⇔ m ≥ −1
Vậy để phương trình đã cho có nghiệm thì m ≥ −1
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
Tìm điều kiện của tham số m để phương trình
(
m
+
2
)
x
2
+
2
x
+
m
0
vô nghiệm A.
m
≥
1
+
2
m
≤
1...
Đọc tiếp
Tìm điều kiện của tham số m để phương trình ( m + 2 ) x 2 + 2 x + m = 0 vô nghiệm
A. m ≥ 1 + 2 m ≤ 1 − 2
B. m > − 1 + 2 m < − 1 − 2
C. 1 − 2 ≤ m ≤ 1 + 2
D. 1 − 2 < m < 1 + 2
Phương trình (m + 2)x2 + 2x + m = 0 (a = m + 2; b = 2; c = m)
TH1: m + 2 = 0 ⇔ m = −2 ta có phương trình 2x – 2 = 0 ⇔ x = 1
TH2: m + 2 ≠ 0 ⇔ m ≠ −2
Ta có ∆ = 22 – 4(m + 2). m = −4m2 – 8m + 4
Để phương trình đã cho vô nghiệm thì:
m ≠ 2 − 4 m 2 − 8 m + 4 < 0 ⇔ m ≠ 2 2 − m + 1 2 < 0
⇔ m ≠ 2 m + 1 2 > 2 ⇔ m ≠ 2 m + 1 > 2 m + 1 < − 2
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Cho phương trình x²-2x+m-3=0 a) tìm điều kiện của m để phương trình có nghiệm số b)tìm m để phương trình trên có 2 nghiệm x1;x2 thỏa điều kiện x1-x2=4
a: Để phương trình có nghiệm thì (-2)^2-4(m-3)>=0
=>4-4m+12>=0
=>-4m+16>=0
=>-4m>=-16
=>m<=4
b: x1-x2=4
x1+x2=2
=>x1=3; x2=-1
x1*x2=m-3
=>m-3=-3
=>m=0(nhận)
Đúng 0
Bình luận (0)
Tìm điều kiện của tham số m để phương trình m x 2 + 2 ( m + 1 ) x + 1 = 0 có nghiệm
A. m ≠ 0
B. m < 0
C. m > 0
D. m ∈ ℝ
Phương trình mx2 + 2(m + 1)x + 1 = 0 (a = m; b = 2 (m + 1); c = 1)
TH1: m = 0 ta có phương trình 2x + 1 = 0
⇔ x = − 1 2 nên nhận m = 0 (1)
TH2: m ≠ 0, ta có = 4(m + 1)2 – 4m.1 = 4m2 + 4m + 4
= 4m2 + 4m + 1 + 3= (2m + 1)2 + 3
Để phương trình đã cho có nghiệm thì
∆ ≥ 0 ⇔ (2m + 1)2 + 3 ≥ 0
⇔ (2m + 1)2 ≥ −3 (luôn đúng với mọi m) (2)
Từ (1) và (92) ta thấy phương trình đã cho có nghiệm với mọi m ∈ ℝ
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Tìm các giá trị của tham số m để phương trình x2-(2m-3)x+m(m-3)=0 có 2 nghiệm phân biệt x1, x2 thỏa mãn điều kiện 2x1-x2=4
Tìm điều kiện của tham số m để bất phương trình (m2-4)x2+2(m-2)x-10≥0 có nghiệm
Tìm điều kiện của tham số m để phương trình
cos
2
x
-
4
cos
x
+
m
0
có nghiệm.
Đọc tiếp
Tìm điều kiện của tham số m để phương trình
cos 2 x - 4 cos x + m = 0 có nghiệm.
![]()
![]()
![]()
![]()
Tìm tất các giá trị của tham số m để phương trình x ^ 2 - 2x - m ^ 2 - 2m - 1 = 0 có hai nghiệm phân biệt x_{1} x_{2} thỏa mãn điều kiện 2x_{1} ^ 2 - x_{2} ^ 2 - x_{1}*x_{2} - 8 = 0
Tìm điều kiện của tham số m để phương trình mx2 + (m - 1)x + 3 - 4m = 0 có hai nghiệm phân biệt x1, x2 thoả mãn x1 < 2 < x2
\(mx^2+\left(m-1\right)x+3-4m=0\left(1\right)\)
\(m=0\Rightarrow\)\(\left(1\right)\Leftrightarrow-x+3=0\Leftrightarrow x=3\left(ktm\right)\)
\(m\ne0\Rightarrow x1< 2< x2\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\\left(x1-2\right)\left(x2-2\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)^2-4m\left(3-4m\right)>0\\x1x2-2\left(x1+x2\right)+4< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>\dfrac{7+4\sqrt{2}}{17}\\m< \dfrac{7-4\sqrt{2}}{17}\end{matrix}\right.\\\dfrac{3-4m}{m}-2.\left(\dfrac{1-m}{m}\right)+4< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>\dfrac{7+4\sqrt{2}}{17}\\m< \dfrac{7-4\sqrt{2}}{17}\end{matrix}\right.\\-\dfrac{1}{2}< m< 0\\\end{matrix}\right.\)\(\Rightarrow m\in\phi\)
Đúng 0
Bình luận (0)