\( x^4-2x^2-400x-9999=0 \)

\(\Leftrightarrow\)\( x^4+11x^3+ 119x^2+909x-11.(x^3+11x^2 +119x+909)=0 \)

\(\Leftrightarrow\) \((x-11).(x^3+11x^3 +119x+909)=0 \)

\(\Leftrightarrow\)\((x-11).(x^3+2x^2+ 101x+9x^2+ 18x+909)=0 \)

\(\Leftrightarrow\) \((x-11).(x+9).(x^2+ 2x+101)=0 \)

Vậy nghiệm của pt là \(11\) và \(-9\)

\(\frac{x+4}{\left(x-2\right)\left(2x-1\right)}+\frac{x+1}{\left(x-3\right)\left(2x-1\right)}=\frac{2x+5}{\left(x-3\right)\left(2x-1\right)}\)

\(\frac{\left(x-3\right)\left(x+4\right)}{\left(x-2\right)\left(2x-1\right)\left(x-3\right)}+\frac{\left(x+1\right)\left(x-2\right)}{\left(x-3\right)\left(2x-1\right)\left(x-2\right)}=\frac{\left(2x+5\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)\left(2x-1\right)}\)

\(\Rightarrow x^2+x-12+x^2-x-2=2x^2+x-10\Leftrightarrow x=-4\)

\(\frac{x+4}{2x^2-5x+2}+\frac{x+1}{2x^2-7x+3}=\frac{2x+5}{2x^2-7x+3}\)

\(\Rightarrow\frac{x+4}{2x^2-5x+2}=\frac{2x-5}{2x^2-7x+3}-\frac{x+1}{2x^2-7x+3}\)

\(\Rightarrow\frac{x+4}{2x^2-5x+2}=\frac{x+4}{2x^2-7x+3}\)

TH1:\(x+4\ne0\)

\(\Rightarrow2x^2-5x+2=2x^2-7x+3\)

\(\Rightarrow-5x+2=-7x+3\)

\(\Rightarrow2x=1\)

\(\Rightarrow x=\frac{1}{2}\)

TH2:\(x+4=0\)

\(\Rightarrow x=-4\)

\(x^4-2x^2-400x-9999=0\Leftrightarrow x^4-11x^3+11x^3-121x^2+119x^2-1309x+909x-9999=0\)

\(\left(x-11\right)\left(x^3+11x^2+119x+909\right)=0\\ \Leftrightarrow\left(x-11\right)\left(x^3+9x^2+2x^2+18x+101x+909\right)=0\)

\(\left(x-11\right)\left(x+9\right)\left(x^2+2x+101\right)=0\)

 nên x=11

       x=-9

X^4-2x^2-400x-9999 <=>x^4+11x^3-11x^3+119x^2-121x^2+909x-1309x-9999=0 <=>x^4+11x^3+119x^2+909x-11(x^3+11x^2+119x+9999)<=>(x-11)(x^3+11x^2+119x+909)   . Phân tích tiếp ta được (x-11)(x+9)(x^2+2x+101)

(x + 2)( x 2  – 3x + 5) = (x + 2) x 2

⇔ (x + 2)( x 2  – 3x + 5) – (x + 2) x 2 = 0

⇔ (x + 2)[( x 2  – 3x + 5) –  x 2 ] = 0

⇔ (x + 2)( x 2  – 3x + 5 –  x 2 ) = 0

⇔ (x + 2)(5 – 3x) = 0

⇔ x + 2 = 0 hoặc 5 – 3x = 0

x + 2 = 0 ⇔ x = -2

5 – 3x = 0 ⇔ x = 5/3

Vậy phương trình có nghiệm x = -2 hoặc x = 5/3

Đáp án đúng : C

Bài 2:

a: =>2x^2-4x+1=x^2+x+5

=>x^2-5x-4=0

=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)

b: =>11x^2-14x-12=3x^2+4x-7

=>8x^2-18x-5=0

=>x=5/2 hoặc x=-1/4

Điều kiện xác định: x ≠ ±2.

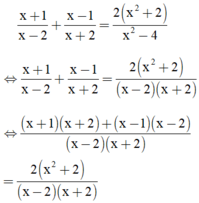
⇒ (x + 1)(x + 2) + (x – 1)(x – 2) = 2(x2 + 2)

⇔ x2 + x + 2x + 2 + x2 – x – 2x + 2 = 2x2 + 4

⇔ 2x2 + 4 = 2x2 + 4

⇔ 0x = 0.

Vậy phương trình nghiệm đúng với mọi x ≠ ±2.