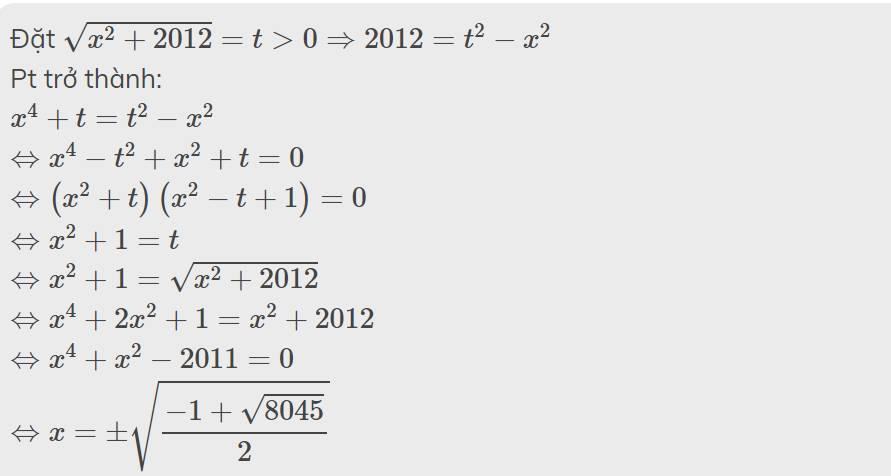Đặt \(\sqrt{x^2+2012}=t>0\Rightarrow2012=t^2-x^2\)

Pt trở thành:

\(x^4+t=t^2-x^2\)

\(\Leftrightarrow x^4-t^2+x^2+t=0\)

\(\Leftrightarrow\left(x^2+t\right)\left(x^2-t+1\right)=0\)

\(\Leftrightarrow x^2+1=t\)

\(\Leftrightarrow x^2+1=\sqrt{x^2+2012}\)

\(\Leftrightarrow x^4+2x^2+1=x^2+2012\)

\(\Leftrightarrow x^4+x^2-2011=0\)

\(\Leftrightarrow x=\pm\sqrt{\dfrac{-1+\sqrt{8045}}{2}}\)

\(x^4+\sqrt{x^2+2012}=2012.\)

\(\Leftrightarrow x^4=-\sqrt{x^2+2012}+2012.\)

\(\Leftrightarrow x^4+x^2+\frac{1}{4}=x^2+2012-\sqrt{x^2+2012}+\frac{1}{4}.\)

\(\Leftrightarrow\left(x^2+\frac{1}{2}\right)^2=\left(\sqrt{x^2+2012}-\frac{1}{2}\right)^2.\)

Đến đây chia 2 TH ra là ok

thank nhé

\(\Leftrightarrow\left(x^2+\frac{1}{2}\right)^2-\left(\sqrt{x^2+2012}-\frac{1}{2}\right)^2=0..\)

HĐT nha hoặc khai phương cx đc

1

Tham khảo:

\(\hept{\begin{cases}\left(x+\sqrt{x^2+2012}\right)\left(y+\sqrt{y^2+2012}\right)=2012\left(1\right)\\x^2+z^2-4\left(y+z\right)+8=0\left(2\right)\end{cases}}\)

Ta có:(1) \(\Leftrightarrow\left(x+\sqrt{x^2+2012}\right)\left(y+\sqrt{y^2+2012}\right)\left(\sqrt{y^2+2012}-y\right)\)\(=2012\left(\sqrt{y^2+2012}-y\right)\)(Do \(\sqrt{y^2+2012}-y\ne0\forall y\))

\(\Leftrightarrow2012\left(x+\sqrt{x^2+2012}\right)=2012\left(\sqrt{y^2+2012}-y\right)\)

\(\Leftrightarrow x+\sqrt{x^2+2012}=\sqrt{y^2+2012}-y\)\(\Leftrightarrow x+y=\sqrt{y^2+2012}-\sqrt{x^2+2012}\)

\(\Leftrightarrow x+y=\)\(\frac{\left(\sqrt{y^2+2012}+\sqrt{x^2+2012}\right)\left(\sqrt{y^2+2012}-\sqrt{x^2+2012}\right)}{\sqrt{y^2+2012}+\sqrt{x^2+2012}}\)

\(\Leftrightarrow x+y=\frac{y^2-x^2}{\sqrt{y^2+2012}+\sqrt{x^2+2012}}\)\(\Leftrightarrow\left(x+y\right)\frac{\sqrt{y^2+2012}-y+\sqrt{x^2+2012}+x}{\sqrt{y^2+2012}+\sqrt{x^2+2012}}=0\)

Do \(\hept{\begin{cases}\sqrt{y^2+2012}>\sqrt{y^2}=\left|y\right|\ge y\forall y\\\sqrt{x^2+2012}>\sqrt{x^2}=\left|x\right|\ge-x\forall x\end{cases}}\)\(\Rightarrow\sqrt{y^2+2012}-y+\sqrt{x^2+2012}+x>0\forall x,y\Rightarrow x+y=0\)

\(\Rightarrow y=-x\)

Thay y = -x vào (2), ta được: \(x^2+z^2+4x-4z+8=0\)

\(\Leftrightarrow\left(x+2\right)^2+\left(z-2\right)^2=0\Leftrightarrow\hept{\begin{cases}x=-2\\z=2\end{cases}}\Rightarrow y=-x=2\)

Vậy hệ có nghiệm \(\left(x;y;z\right)=\left(-2;2;2\right)\)

a) \(P=\dfrac{x^2-\sqrt[]{x}}{x+\sqrt[]{x}+1}-\dfrac{2x+\sqrt[]{x}}{\sqrt[]{x}}+\dfrac{2\left(x+\sqrt[]{x}-2\right)}{\sqrt[]{x}-1}\)

Điều kiện xác định \(\Leftrightarrow\left\{{}\begin{matrix}x>0\\\sqrt[]{x}-1\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x>0\\x\ne1\end{matrix}\right.\)

\(\Rightarrow P=\dfrac{\sqrt[]{x}\left[\left(\sqrt[]{x}\right)^3-1\right]}{x+\sqrt[]{x}+1}-\dfrac{\sqrt[]{x}\left(2\sqrt[]{x}+1\right)}{\sqrt[]{x}}+\dfrac{2\left(\sqrt[]{x}-1\right)\left(\sqrt[]{x}+2\right)}{\sqrt[]{x}-1}\)

\(\Rightarrow P=\dfrac{\sqrt[]{x}\left(\sqrt[]{x}-1\right)\left(x+\sqrt[]{x}+1\right)}{x+\sqrt[]{x}+1}-\left(2\sqrt[]{x}+1\right)+2\left(\sqrt[]{x}+2\right)\)

\(\Rightarrow P=\sqrt[]{x}\left(\sqrt[]{x}-1\right)-\left(2\sqrt[]{x}+1\right)+2\left(\sqrt[]{x}+2\right)\)

\(\Rightarrow P=x-\sqrt[]{x}-2\sqrt[]{x}-1+2\sqrt[]{x}+4\)

\(\Rightarrow P=x-\sqrt[]{x}+3\)

b) \(A=\dfrac{P}{2012\sqrt[]{x}}=\dfrac{x-\sqrt[]{x}+3}{2012\sqrt[]{x}}\)\(\)

\(=\dfrac{x-\sqrt[]{x}+\dfrac{1}{4}-\dfrac{1}{4}+3}{2012\sqrt[]{x}}\)

\(=\dfrac{\left(\sqrt[]{x}-\dfrac{1}{2}\right)^2+\dfrac{11}{4}}{2012\sqrt[]{x}}\)

\(\Rightarrow A=\dfrac{\left(\sqrt[]{x}-\dfrac{1}{2}\right)^2}{2012\sqrt[]{x}}+\dfrac{\dfrac{11}{4}}{2012\sqrt[]{x}}=\dfrac{\left(\sqrt[]{x}-\dfrac{1}{2}\right)^2}{2012\sqrt[]{x}}+\dfrac{11}{4.2012\sqrt[]{x}}\)

Ta lại có  \(\dfrac{\left(\sqrt[]{x}-\dfrac{1}{2}\right)^2}{2012\sqrt[]{x}}\ge0,\forall x\ne0\)

\(\dfrac{1}{\sqrt[]{x}}>0\Rightarrow\dfrac{11}{4.2012\sqrt[]{x}}\ge\dfrac{11}{4.2012}=\dfrac{11}{8048}\)

\(\Rightarrow A=\dfrac{\left(\sqrt[]{x}-\dfrac{1}{2}\right)^2}{2012\sqrt[]{x}}+\dfrac{11}{4.2012\sqrt[]{x}}\ge\dfrac{11}{8048}\)

Dấu "=" xảy ra \(\Leftrightarrow\sqrt[]{x}=1\Leftrightarrow x=1\)

Vậy \(GTNN\left(A\right)=\dfrac{11}{8048}\left(tạix=1\right)\)

\(P=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+\dfrac{2\left(x+\sqrt{x}-2\right)}{\sqrt{x}-1}\)

\(=\dfrac{\sqrt{x}\left(x\sqrt{x}-1\right)}{x+\sqrt{x}+1}-\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}+\dfrac{2\left(\sqrt{x}-1\right).\left(\sqrt{x}+2\right)}{\sqrt{x}-1}\)

\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{x+\sqrt{x}+1}-\left(2\sqrt{x}+1\right)+2.\left(\sqrt{x}+2\right)\)

\(=x-\sqrt{x}+3\)

b) \(\dfrac{P}{2012\sqrt{x}}=\dfrac{x-\sqrt{x}+3}{2012\sqrt{x}}=\dfrac{\sqrt{x}}{2012}-\dfrac{1}{2012}+\dfrac{3}{2012\sqrt{x}}\)

\(=\left(\dfrac{\sqrt{x}}{2012}+\dfrac{3}{2012\sqrt{x}}\right)-\dfrac{1}{2012}\)

\(\ge2\sqrt{\dfrac{\sqrt{x}.3}{2012^2\sqrt{x}}}-\dfrac{1}{2012}\) (BĐT Cauchy)

\(=\dfrac{2\sqrt{3}}{2012}-\dfrac{1}{2012}=\dfrac{2\sqrt{3}-1}{2012}\)

Dấu "=" xảy ra khi \(\dfrac{\sqrt{x}}{2012}=\dfrac{3}{2012\sqrt{x}}\Leftrightarrow x=3\)(tm)