Tam giác ABC cân có AB=AC= 8cm. Đường trung tuyến BD=6cm. Nếu BC^2 = x cm. Tìm x

Những câu hỏi liên quan
Tam giác ABC cân có AB=AC= 8cm. Đường trung tuyến BD=6cm. Nếu BC^2 = x cm. Tìm x
Cho tam giác ABC có AB=6cm ; AC=8cm :=;BC=10cm
a)CM: tam giác ABC vuông tại A
b)vẽ tia BD là PG của góc ABC ( D thuộc AC) , qua điểm D kẻ đường thẳng DE vuông góc BC (E thuộc BC) và cắt đường thẳng AB tại F . CM: tam giác FDC cân
a) Ta có: \(BC^2=10^2=100\)
\(AB^2+AC^2=6^2+8^2=100\)
Do đó: \(BC^2=AB^2+AC^2\)(=100)
Xét ΔABC có \(BC^2=AB^2+AC^2\)(cmt)
nên ΔABC vuông tại A(Định lí Pytago đảo)
b) Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔBAD=ΔBED(cạnh huyền-góc nhọn)
Suy ra: DA=DE(Hai cạnh tương ứng)
Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE(Cmt)
\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔADF=ΔEDC(Cạnh góc vuông-góc nhọn kề)
Suy ra: DF=DC(Hai cạnh tương ứng)
Xét ΔDFC có DF=DC(cmt)
nên ΔDFC cân tại D(Định nghĩa tam giác cân)
Đúng 2
Bình luận (0)
Cho tam giác ABC có AB=AC=5cm, BC=6cm. Đường trung tuyến AM.
a, Cm: tam giác AMB= tam giác AMC
b, Tính độ dài trung tuyến AM.
c, Gọi H là trung điểm của AM. Cm: tam giác BHC là tam giác cân
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: BM=CM=3cm
=>AM=4cm
c: Xét ΔHBC có
HM vừa là đường cao, vừa là trung tuyến
=>ΔHBC cân tại H
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=6cm,AC=8cm và các đường trung tuyến BD,CE vuông góc với nhau .độ dài đoạn BC bằng bao nhiêu
Gọi G là trong tâm
GE = x => CG =2x ; GD =y =>BG =2y
=> pi ta go
\(\int^{x^2+4y^2=16}_{y^2+4x^2=9}\Leftrightarrow5\left(x^2+y^2\right)=25\Leftrightarrow4x^2+4y^2=\frac{5}{4}=BC^2\Leftrightarrow BC=\frac{\sqrt{5}}{2}\)
Đúng 0
Bình luận (0)
cho tam giác ABC có AB=6cm, BC=10cm, AC=8cm
a, CM tam giác ABC vuông
b, Vẽ đường cao AH của tam giác ABC và phân giác AD của tam giác AHC. CM tam giác ABD là tam giác cân tại B
c, Vẽ phân giác AE của tam giác ABH. CM BD^2+CH^2=CE^2+BH^2
d, CM giao điểm của các đường trung trực của tam giác ADE cách đều 3 cạnh của tam giác ABC
Cho tam giác ABC co AB = 6cm, AC = 8cm, các đường trung tuyến BD và CE vuông góc với nhau. Tính độ dài BC
bạn Dinh dang nam nói láo ,bạn ko trả lời giúp thì
đừng chửi Dang huynh
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1. Cho tam giác ABC có AB=6cm, AC=8cm .Các đường trung tuyến BD và CE vuông góc với nhau. Tính BC.
2. Cho tam giác ABC vuông cân tại A, đường trung tuyến BM. Gọi D là hình chiếu của C trên BM. Gọi D là hình chiếu của C trên BM, H là hình chiếu của D trên AC. Chứng minh : AH=3HD
cảm ơn các bạn trước nhaaa
Cho tam giác ABC có đường trung tuyến AM và đường phân giác AD của góc BAˆ. Biết AB 12 cm; AC 8cm và BC 15cm. Tính tỉ số BM/BD A.
5
6
B.
7
6
C.
1
6
D.
3
4
Đọc tiếp
Cho tam giác ABC có đường trung tuyến AM và đường phân giác AD của góc BAˆ. Biết AB = 12 cm; AC = 8cm và BC = 15cm. Tính tỉ số BM/BD
A. 5 6
B. 7 6
C. 1 6
D. 3 4
Do M là trung điểm của BC nên:
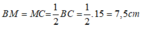
Theo tính chất tia phân giác của góc ta có:
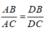
Suy ra:
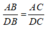
Theo tính chất của dãy tỉ số bằng nhau ta có:
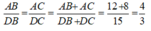
Suy ra:
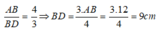
Do đó:
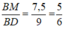
Chọn đáp án A
Đúng 0
Bình luận (0)
Cho tam giác ABC có đường trung tuyến AM và đường phân giác AD của góc BAˆ. Biết AB = 12 cm; AC = 8cm và BC = 15cm. Tính tỉ số BM/BD.
A. 5 6
B. 7 6
C. 1 6
D. 3 4
Do M là trung điểm của BC nên:
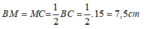
Theo tính chất tia phân giác của góc ta có:
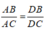
Suy ra:
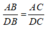
Theo tính chất của dãy tỉ số bằng nhau ta có:
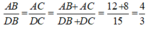
Suy ra:
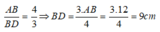
Do đó:
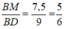
Chọn đáp án A
Đúng 0
Bình luận (0)
















