Cho tam giác ABC vuông tại C trong đó ac =15cm ;góc b =30° a, vẽ hình
B, hãy giải tam giác vuông ABC
cho tam giác ABC vuông tại A có AB/AC=0,75 và BC=15cm .khi đó chu vi của tam giác ABC là...
Cho tam giác ABC vuông tại A có BC = 15cm,AC=12cm.Khi đó AB bằng
A .81cm B.27cm C.9cm D.3cm
Cho tam giác ABC vuông tại A,Giải tam giác ABC biết
a,AC=15cm góc C=35 độ
b,AB=8cm,góc C=50 độ
a: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}=55^0\)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}\)
=>\(BC=15:sin55\simeq18.31\left(cm\right)\)
\(AB=\sqrt{BC^2-AC^2}\simeq10,5\left(cm\right)\)
b: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}=90^0-50^0=40^0\)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}\)
=>\(BC=8:sin50\simeq10,44\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq6,71\left(cm\right)\)
Cho tam giác ABC vuông tại A có AC= 12cm, BC=15cm. Giải tam giác ABC?
ΔABC vuông tại A
=>AB^2+AC^2=BC^2
=>AB^2=15^2-12^2=81
=>AB=9cm
Xét ΔABC vuông tại A có sin C=AB/BC=9/15=3/5
nên góc C=37 độ
=>góc B=53 độ
Xét tam giác ABC vuông tại A áp dụng Py-ta-go ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AB=\sqrt{BC^2-AC^2}\)
\(\Leftrightarrow AB=\sqrt{15^2-12^2}=9\left(cm\right)\)
Xét tam giác ABC vuông tại A ta có:
\(sinC=\dfrac{AB}{BC}=\dfrac{9}{15}=\dfrac{3}{5}\)
\(\Rightarrow\widehat{C}\approx37^o\)
Mà: \(\widehat{C}+\widehat{B}=90^o\)
\(\Leftrightarrow\widehat{B}=90^o-37^o=53^o\)
Cho tam giác ABC vuông tại A, có AB = 10cm và AC = 15cm
a, Tính góc B
b, Phân giác trong góc B cắt AC tại I . Tính AI
c, Vẽ AH vuông góc BI tại H . Tính AH
a) Ta có : \(BC=\sqrt{AB^2+AC^2}=\sqrt{10^2+15^2}=5\sqrt{13}\) (cm)
\(sinB=\frac{AC}{BC}=\frac{15}{5\sqrt{13}}=\frac{3}{\sqrt{13}}\Rightarrow\widehat{B}\approx56^o18'35,76''\)
b) Đặt AI = x (0<x<15)
Theo t/c đường phân giác ,ta có \(\frac{AI}{AB}=\frac{IC}{BC}\) hay \(\frac{x}{10}=\frac{15-x}{5\sqrt{13}}\Leftrightarrow x=\frac{10\sqrt{13}-20}{3}\) (cm)
c) Tính được : \(BI=\sqrt{AB^2+AI^2}=\sqrt{10^2+\left(\frac{10\sqrt{13}-20}{3}\right)^2}\) (cm)
Lại có : AB . AI = BI . AH => \(AH=\frac{AB.AI}{BI}=............\)
Câu 3: (3,0 điểm) Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC tại D. Kẻ DE vuông góc với BC tại E.
a) Chứng minh: tam giác ABD= tam giác EBD từ đó suy ra AB = EB.
b) Cho AB = 12cm, AC = 15cm. Tính độ dài cạnh BC.
c) Cho góc B = 600. Tính góc ADE .
d) Chứng minh: DA < DC.
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó:ΔABD=ΔEBD
Suy ra: BA=BE
b: \(BC=\sqrt{12^2+15^2}=3\sqrt{41}\left(cm\right)\)
c: \(\widehat{ADE}=180^0-60^0=120^0\)
d: Ta có: DA=DE
mà DE<DC
nên DA<DC
Cho tam giác ABC vuông tại A và BD là phân giác trong của góc B (D thuoc AC). Biết DB= 7cm, DC= 15cm, khi đó AD=... cm. ?
Cho tam giác ABC vuông tại A có AB : AC = 4 : 5 và đường cao AH bằng 12cm. Khi đó độ dài đoạn thẳng HB bằng
A. 6cm; B. 9,6cm; C. 12cm; D. 15cm.
Hãy chọn phương án đúng.
*Trong các bài (1.3, 1.4, 1.5) ta sẽ sử dụng các kí hiệu sau đây đối với tam giác ABC vuông tại A có đường cao AH:
AB = c, AC = b, BC = a, AH = h, BH = c’, CH = b’.
Hướng dẫn:
∆
ABC ∼
∆
HBA nên 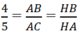
Suy ra HB = 4/5HA = 48/5 = 9,6. Chọn B.
Cho tam giác ABC vuông tại A, AB = 15cm; AC = 20cm. Phân giác của góc A cắt BC tại E.
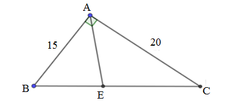
Giải tam giác ABC:
A. BC = 25; B ^ = 36 0 52 ' ; C ^ = 53 0 8 '
B. BC = 25; B ^ = 53 0 8 ' ; C ^ = 53 0 8 '
C. BC = 25; B ^ = 36 0 52 ' ; C ^ = 53 0 8 '
D. BC = 25; B ^ = 36 0 52 ' ; C ^ = 53 0 8 '
Áp dụng định lý Pytago cho vuông tại A có:
![]()
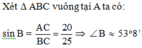

Đáp án cần chọn là: B
Cho tam giác ABC vuông ở C có AC=9cm, AB=15cm. Từ trung điểm M của AB kẻ đường thẳng vuông góc với AB, cắt BC và AC lần lượt ở P và Q.
a) CM : tam giác ABC đồng dạng với tam giác AQM; từ đó suy ra AB mũ 2 =2.AC.AQ
b) Tính PQ.
c) tia AP cắt BQ tại N. CM : CN song song với AB.
d) tính diện tích ABNC.