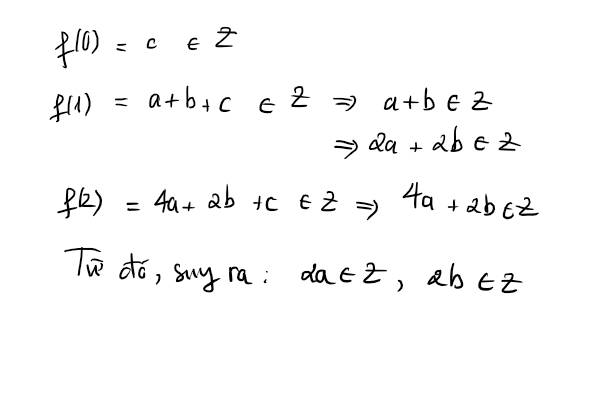Cho đa thức:f(x)=a\(\times x^2\)+b\(\times x\)+c với a,b,c\(\in Q\).Chứng minh rằng f(-2);f(3) \(\le0\) biết 13a+b+2c=0

Những câu hỏi liên quan
a)Cho B=x^2 - 3xy + 2y^2 +x và x-y=1. Tính giá trị của đa thức B
b) Cho đa thức f(x) = ax^2 +bx+ c với a,b,c là các hệ số thoả mãn 13a +b +2c. Chứng tỏ rằng: f(-2) × f(-3) bé hơn hoặc bằng 0
P(x) = 2×2 + 2x – 6×2 + 4×3 + 2 – x3
Q(x) = 3 – 2×4 + 3x + 2×4 + 3×3 – x
a) Thu gọn và sắp xếp đa thức P(x) và Q(x) theo lũy thừa giảm dần của biến
b) Tìm đa thức C(x) biết C(x) = P(x) + Q(x)
c) Chứng minh đa thức D(x) = Q(x) – P(x) vô nghiệm
a)\(P\left(x\right)=2.2+2x-6.2+4.3+2-3x\)
\(=4+2x-12+12+2-3x\)
\(=\left(2x-3x\right)+\left(4+12+2\right)\)
\(=\left(-x\right)+18\)
\(Q\left(x\right)=3-2.4+3x+2.4+3.3-x\)
\(=3-8+3x+8+9-x\)
\(=\left(3x-x\right)+\left(3-8+8+9\right)\)
\(=2x+12\)
b)\(C\left(x\right)=P\left(x\right)+Q\left(x\right)\)
\(\Rightarrow C\left(x\right)=\left(-x+18\right)+\left(2x+12\right)\)
\(C\left(x\right)=-x+18+2x+12\)
\(C\left(x\right)=\left(-x+2x\right)+\left(18+12\right)\)
\(C\left(x\right)=x+26\)
c)\(D\left(x\right)=Q\left(x\right)-P\left(x\right)\)
\(\Rightarrow D\left(x\right)=\left(2x+12\right)-\left(-x+18\right)=\)
\(D\left(x\right)=2x+12+x+18\)
\(D\left(x\right)=\left(2x+x\right)+\left(12+18\right)\)
\(D\left(x\right)=3x+26\)
Có \(3x\) luôn \(\ge0\) và \(\le0\) với mọi x.
Lại có 26>0; \(26⋮̸3\)
\(\Rightarrow\)D(x) vô nghiệm
Đúng 0
Bình luận (0)
Cho đa thức:f(x)=\(ax^2\)+bx+c với a,b,c là các số thực.Biết f(0),f(1),f(2) có giá trị nguyên.Chứng minh 2a,2b có giá trị nguyên
cho đa thức f(x) xác định với mọi x thoả mãn:
\(x\times f\left(x+2\right)=\left(x^2-9\right)\times f\left(x\right)\)
1) tính f(5)
2) chứng minh rằng f(x) có ít nhất 3 nghiệm
1) Thay x=3 vào đẳng thức, thu được:
\(3\times f\left(3+2\right)=\left(3^2-9\right)\times f\left(3\right)\)
\(\Leftrightarrow\) \(3\times f\left(5\right)=0\times f\left(3\right)=0\)
\(\Leftrightarrow\) \(f\left(5\right)=0\)
2) Ta đã chứng minh x=5 là nhiệm của f(x)\(\Rightarrow\)Cần chứng minh f(x) có 2 nghiệm nữa
Thay x=0 Vào đẳng thức, thu được\(0\times f\left(0+2\right)=\left(0^2-9\right)\times f\left(0\right)\)
\(\Leftrightarrow\) \(f\left(0\right)=0\)
\(\Rightarrow\)x=0 là ngiệm của f(x)
Thay x=-3 và đẳng thức, thu được\(-3\times f\left(-3+2\right)=\left(\left(-3\right)^2-9\right)\times f\left(-3\right)\)
\(\Leftrightarrow\)\(-3\times f\left(-1\right)=0\times f\left(-3\right)=0\)
\(\Leftrightarrow\)\(f\left(-1\right)=0\)
\(\Rightarrow\)x=-1 là nghiệm của f(x)
Vậy f(x) có ít nhất 3 nghiệm là x=5; x=0; x=-1
Cho đa thức f(x) = ax2 + bx + c. Trong đó a,b,c là các hệ số nguyên. Biết rằng f(x) chia hết cho 3 với mọi \(x\in Z\). Chứng minh rằng a, b, c chia hết cho 3.
Lời giải:
Vì $f(x)$ chia hết cho $3$ với mọi \(x\in\mathbb{Z}\) nên ta có:
\(\left\{\begin{matrix} f(0)=c\vdots 3\\ f(1)=a+b+c\vdots 3 3\\ f(-1)=a-b+c\vdots 3\end{matrix}\right.\Rightarrow \left\{\begin{matrix} c\vdots 3\\ a+b\vdots 3(1)\\ a-b\vdots 3 (2) \end{matrix}\right.\)
Từ \((1),(2)\Rightarrow 2a\vdots 3\). Mà $2$ không chia hết cho $3$ nên $a$ chia hết cho $3$
Có $a+b$ chia hết cho $3$ và $a$ chia hết cho $3$ nên $b$ cũng chia hết cho $3$
Do đó ta có đpcm
Đúng 0
Bình luận (0)
Đề cương cuối hk2 trường gia Lạc của tui mà ko bt lam Câu1:
Tìm đa thứcM biết
a,M(x2y-1)-2X3 +X2Y+1
b,3X2+3xy-x3-M 3X2+3XY-4y2
C3:cHO ĐA THƯC Sau P(x)X3+3x2+3xz
Q(x)x3-x2-5x+2
a,TINH P(x) +Q(×),,,,,,,,b TINH P(X)-Q(×)
C.TIM NGHIEM CUa ĐA thức H (×)P(×) +Q(×)
C5:
Cho 2 đa ThứC F(×)2x2+ax+4 và g(×)x-5x-b
CO b,c làhằng số tìm Các Hệ Số a,b SAo Cho f(×} g(×) và f-1và g(5)
Đọc tiếp
Đề cương cuối hk2 trường gia Lạc của tui mà ko bt lam Câu1:
Tìm đa thứcM biết
a,M=(x2y-1)=-2X3 +X2Y+1
b,3X2+3xy-x3-M= 3X2+3XY-4y2
C3:cHO ĐA THƯC Sau P(x)=X3+3x2+3xz
Q(x)=x3-x2-5x+2
a,TINH P(x) +Q(×),,,,,,,,b TINH P(X)-Q(×)
C.TIM NGHIEM CUa ĐA thức H (×)=P(×) +Q(×)
C5:
Cho 2 đa ThứC F(×)=2x2+ax+4 và g(×)=x-5x-b
CO b,c làhằng số tìm Các Hệ Số a,b SAo Cho f(×}= g(×) và f=-1và g(5)
Cho đa thức f(x) = ax2 +bx + c. Trong đó a, b, c là các hệ số nguyên. Biết rằng f(x) chia hết cho 3 với mọi \(x\in Z\). Chứng minh a,b,c chia hết cho 3
Ta có : \(f\left(x\right)⋮3\) với \(\forall x\in Z\)
\(\Rightarrow f\left(0\right)=a.0^2+b.0+c=0+0+c=c⋮3\)
\(Do\) \(f\left(x\right)⋮3\) với \(\forall x\in Z\)
\(\Rightarrow f\left(1\right)=a.1^2+b.1+c=a+b+c⋮3\left(1\right)\)
\(f\left(-1\right)=a.\left(-1\right)^2+b.\left(-1\right)+c=a-b+c⋮3\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left(a+b+c\right)-\left(a-b+c\right)=a+b+c-a+b-c=2b⋮3\)
Do 2 ko chia hết cho 3 \(\Rightarrow\) Để \(2b⋮3\) thì \(b⋮3\)
Ta lại có : \(a+b+c⋮3\)
mà \(b⋮3\) ; \(c⋮3\)
\(\Rightarrow\) Để tổng trên chia hết cho 3 thì a \(⋮3\)
Vậy a,b,c \(⋮3\)
Đúng 1
Bình luận (2)
1.Cho đa thức f(x)ax2 + bx + c với a, b, c là các hệ số nguyên. Chứng minh: f(x) + f(-x) ⋮ 2 với mọi số nguyên x .
2.Cho đa thức P(x)ax+b (a, b ∈ Z;a ≠0). Chứng minh rằng:/P(2018) - P(1)/ ≥ 2017
3.Cho đa thức f(x) 2x2 + 3x +1.Chứng tỏ f(2n) - f(n) ⋮ 3.
4.Cho đa thức f(x) 5x+1. Với 2 số a và b (ab).
5.Cho đa thức f(x) ax + b với a≠0, a ϵ Z. Chứng tỏ rằng /f (2017) - f(1)/ ≥ 2016.
giúp mình với!!!
Đọc tiếp
1.Cho đa thức f(x)=ax2 + bx + c với a, b, c là các hệ số nguyên. Chứng minh: f(x) + f(-x) ⋮ 2 với mọi số nguyên x .
2.Cho đa thức P(x)=ax+b (a, b ∈ Z;a ≠0). Chứng minh rằng:/P(2018) - P(1)/ ≥ 2017
3.Cho đa thức f(x) =2x2 + 3x +1.Chứng tỏ f(2n) - f(n) ⋮ 3.
4.Cho đa thức f(x) = 5x+1. Với 2 số a và b (a<b).
5.Cho đa thức f(x) = ax + b với a≠0, a ϵ Z. Chứng tỏ rằng /f (2017) - f(1)/ ≥ 2016.
giúp mình với!!!
a,Cho đa thức f(x)=ax+b (a khác 0). Biết f(0)=0, chứng minh rằng F(x)=-f(-x)với mọi x
b,Đa thức f(x)=ax^2=bx+c (a khác 0).Biết F(1)=F(-1), chứng minh rằng f(x) với mọi x