cho hình tam giác abc có ae=ec;bd=1/3bc;diện tích hình tam giác dec là 6cm2 . tính diện tích hình tam giác abc
Những câu hỏi liên quan
Tam giác ABC có chiều cao là 20 cm, cạnh đáy gấp rưỡi chiều cao. D là điểm chính giữa AB. Trên AC lấy điểm E sao cho AE gấp đôi EC. Tính diện tích hình tam giác ABC và diện tích hình tam giác AED?
Cho hình tam giác ABC có diện tích là 90 cm2, D là điểm chính giữa AB. Trên AC lấy điểm E sao cho AE gấp đôi EC. Tính diện tích hình tam giác AED.
Nối C với D.Ta thấy CBD hay CDA =1/2 ABC=ABC:2=90:2=45(cm vuông)
Ta thấy AKD,KED,ECD có chung đường cao và đều có đáy =1/3 đáy AC. Vậy suy ra các hình AKD,KED,ECD=1/3CDA=45:3=15(cm vuông)
AED=2/3 CDA=45x2/3=30 (cm vuông) hoặc AED=ADK+EKD=15+15=30(cm vuông)
Đ/S:30 cm vuông
Đúng 0
Bình luận (0)
Cho tam giác ABC . E là một điểm nằm trên cạnh BC sao cho BE = 1/2 EC . Nối AE . I là một điểm nằm trên cạnh AE sao cho AI = 2/3 AE . Nối và kéo dài BI , cắt cạnh AC tại D . Biết DT hình tam giác AID là 16 cm vuông . Tính DT hình tam giác ABC .
Kết quả bài này là 90 cm2
Giải bài này dài lắm nên mk ko giải ra đc đâu
Đúng 0
Bình luận (0)
cho tam giác ABC . e là một điểm nằm trên cạnh BC sao cho BE = 1/2 EC . nối AE . I là một điểm nằm trên cạnh AE sao cho AI =2/3 AE . Nối và kéo dài BI cắt cạnh AC tại D . Biết diện tích hình tam giác AID là 16 cm2 . Tính diện tích hình tam giác ABC ?
mik đã đc cô giáo dạy bài này rùi nhưng mik ko nhớ cách giải mà nhớ đáp án là 90 cm vuông
Đúng 1
Bình luận (0)
Theo bài ra ta có: BE = 1/2 EC. Suy ra: BE = 1/3 BC
Suy ra:
SABE = 1/3 SABC
SAEC = 2/3 SABC
Theo bài ra ta cũng có: EC = 2/3 BC
Suy ra: SABI = 2/3 SABE
Suy ra:
SABI = (2/3 x 1/3) SABC = 2/9 SABC
SBIE = 1/2 SABI = 1/9 SABC
Ta lại có: SCIE = 2 SBIE
Suy ra: SCIE = 2/9 SABC
Ta có: SBIC = SBIE + SCIE = 1/9 SABC + 2/9 SABC = 3/9 SABC
Hai tam giác ABI và BIC có BI chung nên 2 đường cao tỉ lệ với 2 diện tích và bằng: (2/9) : (3/9) = 2/3. Do 2 đường cao này cũng là 2 đường cao của 2 tam giác AID và CID có chung ID nên ta có: SAID : SCID = 2/3
Suy ra: SCID = 16 : 2/3 = 24 (cm2)
Suy ra: SAIC = SAID + SCID = 16 + 24 = 40 (cm2)
Vì: SAIC = 2/3 SAEC, suy ra: SAEC = 3/2 SAIC = 3/2 x 40 = 60 (cm2)
Vì: SAEC = 2/3 SABC, suy ra: SABC = 3/2 SAIC = 3/2 x 60 = 90 (cm2)
Đúng 0
Bình luận (0)
cho tam giác ABC có diện tích = 90 cm2 . gọi D là điểm giữa cạnh AB. trên cạnh AC lấy E. sao cho AE=2 lần EC. tính diện tích hình tam giác AED
Cho hình tam giác ABC có diện tích 90 m2 .D là điểm chính giữa của AB . Trên AC lấy điểm E sao cho AE gấp đôi EC . Tính diện tích hình tam giác AED
Nối C với D. Ta thấy CBD hay CDA = 1/2 ABC = ABC : 2 = 90 : 2 = 45 ( cm2 )
Ta thấy AKD, KED, ECD có chung đường cao và đều có đáy = 1/3 đáy AC. Vậy suy ra các hình AKD, KED, ECD = 1/3 CDA = 45 : 3
= 15 ( cm2 )
AED = 2/3 CDA = 45 x 2/3 = 30 ( cm2 ) hoặc AED = ADK + EKD = 15 + 15 = 30 ( cm2 )
Đáp số : 30 cm2
Đúng 0
Bình luận (0)
Hình tam giác ABC có diện tích là 90 cm*. Trên cạnh AB lấy điểm D sao cho AD và DB bằng nhau. Trên cạnh AC lấy điểm E sao cho AE gấp đôi EC. Tính diện tích hình tam giác ADE.
Cho tam giác ABC có diện tích bằng 80cm vuông. Gọi D là điểm chính giữa của BC, E là điểm nằm cạnh AC sao cho AE gấp 3 lần EC. Tính diện tích hình tam giác DEC.
cho tam giác ABC có AB<AC.kẻ tia phân giác AD của BAC(D thuộc BC).trên cạnh AC lấy điểm E sao cho AE=AB.trên tia AB lấy điểm F sao cho À=AC.chứng minh:a, tam giác BDF- tam giác EDC b, BF=EC c, AD vuông góc FC . CÓ VẼ HÌNH.
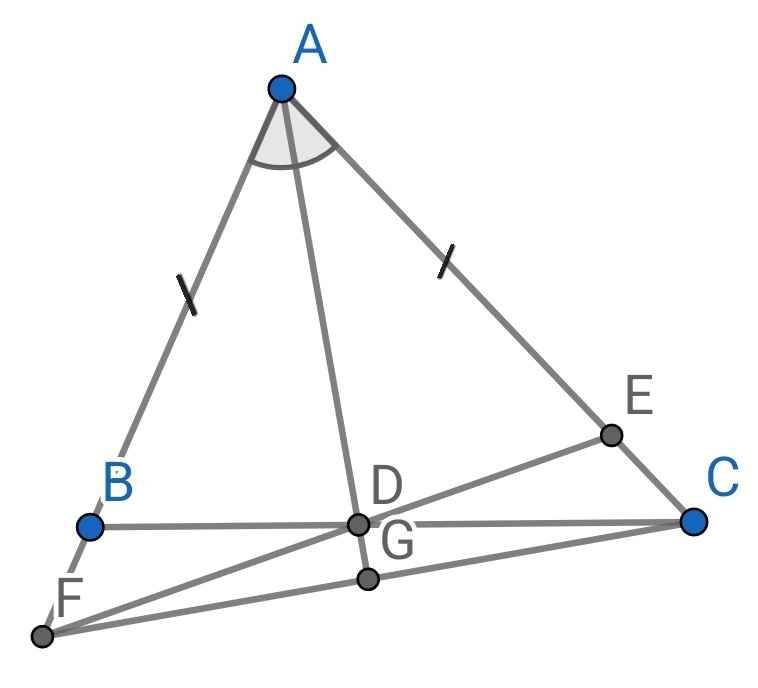a) Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠CAD
⇒ ∠BAD = ∠EAD
Xét ∆ABD và ∆AED có:
AD là cạnh chung
∠BAD = ∠EAD (cmt)
AB = AE (gt)
⇒ ∆ABD = ∆AED (c-g-c)
⇒ BD = ED (hai cạnh tương ứng)
Do ∆ABD = ∆AED (cmt)
⇒ ∠ABD = ∠AED (hai góc tương ứng)
Ta có:
∠ABD + ∠FBD = 180⁰ (kề bù)
∠AED + ∠CED = 180⁰ (kề bù)
Mà ∠ABD = ∠AED (cmt)
⇒ ∠FBD = ∠CED
Xét ∆BDF và ∆EDC có:
BD = ED (cmt)
∠FBD = ∠CED (cmt)
∠BDF = ∠EDC (đối đỉnh)
⇒ ∆BDF = ∆EDC (g-c-g)
b) Do ∆BDF = ∆EDC (cmt)
⇒ BF = EC (hai cạnh tương ứng)
c) Gọi G là giao điểm của AD và CF
AG là tia phân giác của ∠FAC
⇒ ∠FAG = ∠CAG
Xét ∆AFG và ∆ACG có:
AF = AC (gt)
∠FAG = ∠CAG (cmt)
AG là cạnh chung
⇒ ∆AFG = ∆ACG (c-c-c)
⇒ ∠AGF = ∠AGC (hai góc tương ứng)
Mà ∠AGF + ∠AGC = 180⁰ (kề bù)
⇒ ∠AGF = ∠AGC = 180⁰ : 2 = 90⁰
⇒ AG FC
Hay AD ⊥ FC
Đúng 2
Bình luận (0)