S là tập các giá trị m để x2+2mx+5m-8 < 0 có nghiệm là [a;b] sao cho b-a = 4, tổng tất cả các phần tử S là
Những câu hỏi liên quan
a)Có bao nhiêu giá trị nguyên m để hàm số \(y=\sqrt{x^2-2mx-2m+3}\) có tập xác định là R
b) Gọi S là tập hợp các giá trị m để bất pt \(x^2-2mx+5m-8\le0\) có tập nghiệm là [a;b] sao cho b-a=4. Tổng tất cả phần tử S là
Gọi S là tập hợp các giá trị của tham số m để giá trị lớn nhất của hàm số y
x
2
-
m
x
+
2
m
x
-
2
trên đoạn [-1;1] bằng 3. Tính tổng tất cả các phần tử của S. A.
-
8...
Đọc tiếp
Gọi S là tập hợp các giá trị của tham số m để giá trị lớn nhất của hàm số y = x 2 - m x + 2 m x - 2 trên đoạn [-1;1] bằng 3. Tính tổng tất cả các phần tử của S.
A. - 8 3
B. 5
C. 5 3
D. -1
Chọn D
Xét hàm số y =
x
2
-
m
x
+
2
m
x
-
2
trên [-1;1] có: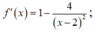 
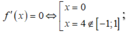
Bảng biến thiên
Trường hợp 1. 
Khi đó
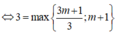
Trường hợp 2. 
Khả năng 1.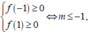 
Khi đó 
Khả năng 2 
Khi đó 
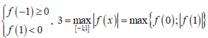
Trường hợp này vô nghiệm.
Khả năng 3. 
Khi đó 
Vô nghiệm.
Vậy có hai giá trị thỏa mãn là 
Do đó tổng tất cả các phần tử của S là -1.
Đúng 0
Bình luận (0)
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc [−20; 20] để phương trình x 2 - 2 m x + 144 = 0 có nghiệm. Tổng của các phần tử trong SS bằng:
A. 21
B. 18
C. 1
D. 0
Phương trình có nghiệm khi ∆ = m 2 - 144 ≥ 0 ⇔ m 2 ≥ 12 2 ⇔ m ≥ 12 m ≤ − 12
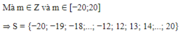
Do đó tổng các phần tử trong tập S bằng 0
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Giup mình câu này với
Gọi S là tập hợp các giá trị m để bpt x2-2mx+5m-8<=0 có tập nghiệm [a;b] sao cho b=a=4. Tổng tất cả các phần tử của S là?
Đề đúng là \(b=a=4\) chứ bạn?
Đúng 0
Bình luận (0)
Tập tất cả các giá trị thức của tham số m để
x
2
+
2
m
x
+
3
m
-
2
≤
0
vô nghiệm là
Đọc tiếp
Tập tất cả các giá trị thức của tham số m để x 2 + 2 m x + 3 m - 2 ≤ 0 vô nghiệm là
Cho hai phương trình:
x
2
-
2
m
x
+
1
0
và
x
2
-
2
x
+
m
0
. Gọi S là tập hợp các giá trị của mm để mỗi nghiệm của phương trình này là nghịch đảo của một nghiệm của phương trình kia. Tổng các phần tử của S gần nhất với số nào dưới đây? A. -1 B. 0 C. 1 D. Một đáp số khác
Đọc tiếp
Cho hai phương trình: x 2 - 2 m x + 1 = 0 và x 2 - 2 x + m = 0 . Gọi S là tập hợp các giá trị của mm để mỗi nghiệm của phương trình này là nghịch đảo của một nghiệm của phương trình kia. Tổng các phần tử của S gần nhất với số nào dưới đây?
A. -1
B. 0
C. 1
D. Một đáp số khác
Gọi x 1 , x 2 là nghiệm của phương trình x 2 - 2 m x + 1 = 0 . Khi đó x 1 + x 2 = 2 m x 1 . x 2 = 1
Gọi
x
3
,
x
4
là nghiệm của phương trình
x
2
-
2
m
x
+
1
=
0
. Khi đó
x
3
+
x
4
=
2
x
3
.
x
4
=
m
Ta có: x 1 = 1 x 3 x 2 = 1 x 4 ⇒ x 1 + x 2 = 1 x 3 + 1 x 4 x 1 . x 2 = 1 x 3 . x 4
⇒ x 1 + x 2 = x 3 + x 4 x 3 . x 4 x 1 . x 2 = 1 x 3 . x 4 ⇔ 2 m = 2 m 1 = 1 m ⇔ m = 1
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
Tập tất cả các giá trị của tham số m để phương trình
x
2
-
2
m
x
+
m
+
2
0
có hai nghiệm dương phân biệt là: A.
2
;
+
∞
B.
-
∞
;
-
2
C. ...
Đọc tiếp
Tập tất cả các giá trị của tham số m để phương trình x 2 - 2 m x + m + 2 = 0 có hai nghiệm dương phân biệt là:
A. 2 ; + ∞
B. - ∞ ; - 2
C. - ∞ ; - 1 ∪ 2 ; + ∞
D. - 1 ; 2
Để phương trình x 2 - 2 m x + m + 2 = 0 có hai nghiệm dương phân biệt
⇔ Δ ' > 0 S > 0 P > 0 ⇔ − m 2 − 1. m + 2 > 0 2 m > 0 m + 2 > 0 ⇔ m 2 − m − 2 > 0 m > 0 m > − 2 ⇔ m < − 1 , m > 2 m > 0 m > − 2
Vậy: m > 2
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Tập tất cả các giá trị của tham số m để phương trình (m-1)x2 -2mx + m + 2 =0 có hai nghiệm trái dấu là
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=4m^2-4\left(m+2\right)\left(m-1\right)\ge0\\x_1x_2=\dfrac{m+2}{m-1}< 0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}-4m+8\ge0\\-2< m< 1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ge2\\-2< m< 1\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
Đúng 1
Bình luận (1)
Gọi S là tập các giá trị thực của m để hàm số y = 2 m x − 8 x − m đồng biến trên khoảng (-1;3). Khi đó tập S là
A. S = (-2;2)
B. S = [-2;2]
C. S = (-2;-1)
D. S = [-2;-1]
