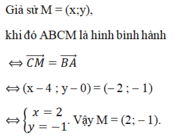Trên mặt phẳng tọa tộ Oxy. Lấy các điểm A (-2;1); B (-6;1); C (-6;6); D (-2;b).Tứ giác ABCD là hình chữ nhật khi đó b =

Những câu hỏi liên quan
Trên mặt phẳng tọa tộ Oxy. Lấy các điểm A (-2;1); B (-6;1); C (-6;6); D (-2;b).Tứ giác ABCD là hình chữ nhật khi đó b = ?
Trên mặt phẳng tọa tộ Oxy. Lấy các điểm A (-2;1); B (-6;1); C (-6;6); D (-2;b).Tứ giác ABCD là hình chữ nhật khi đó b =
Trên mặt phẳng tọa tộ Oxy. Lấy các điểm A (-2;1); B (-6;1); C (-6;6); D (-2;b).Tứ giác ABCD là hình chữ nhật khi đó b =
Trên mặt phẳng tọa tộ Oxy. Lấy các điểm A (-2;1); B (-6;1); C (-6;6); D (-2;b).Tứ giác ABCD là hình chữ nhật khi đó b =
trong mặt phẳng tọa dộ OXY lấy A(2;-1) và B(4;3). Tìm tọa dộ điểm M trên trục hoành sao cho /MA - MB/ đạt giá trị lớn nhất
Trên mặt phẳng tọa độ Oxy, cho điểm A(2; 4). Hãy xác định vị trí tương đối của đường tròn (A; 2) và các trục tọa độ.
Do A(2; 4) nên A cách trục Ox 2 đơn vị, cách trục Oy 4 đơn vị
Khi đó đường tròn (A; 2) tiếp xúc với trục Ox và không giao nhau với trục Oy
Đúng 1
Bình luận (0)
Trên mặt phẳng tọa độ Oxy cho các điểm A(–1; 1); B(1; 2); C(4; 0). Tìm tọa độ điểm M sao cho ABCM là hình bình hành là:
A. M(2; 1)
B. M(2; –1)
C. M(–1; 2)
D. M(1; 2)
Trong mặt phẳng tọa độ
O
x
y
ở góc phần tư thứ nhất ta lấy 2 điểm phân biệt; cứ thế ở các góc phần tư thứ hai, thứ ba, thứ tư ta lần lượt lấy 3, 4, 5 điểm phân biệt (các điểm không nằm trên các trục tọa độ). Trong 14 điểm đó ta lấy 2 điểm bất kỳ. Tính xác suất để đoạn thẳng nối hai điểm đó cắt hai trục tọa độ A.
8
91
B. ...
Đọc tiếp
Trong mặt phẳng tọa độ O x y ở góc phần tư thứ nhất ta lấy 2 điểm phân biệt; cứ thế ở các góc phần tư thứ hai, thứ ba, thứ tư ta lần lượt lấy 3, 4, 5 điểm phân biệt (các điểm không nằm trên các trục tọa độ). Trong 14 điểm đó ta lấy 2 điểm bất kỳ. Tính xác suất để đoạn thẳng nối hai điểm đó cắt hai trục tọa độ
A. 8 91
B. 23 91
C. 68 91
D. 83 91
Chọn B
Lời giải. Không gian mẫu là số cách chọn 2 điểm bất kỳ trong 14 điểm đã cho.
Suy ra số phần tử của không gian mẫu là Ω = C 14 2 = 91 .
Gọi A là biến cố :
Đoạn thẳng nối 2 điểm được chọn cắt hai trục tọa độ.
Để xảy ra biến cố A thì hai đầu đoạn thẳng đó phải ở góc phần tư thứ nhất và thứ ba hoặc phần tư thứ hai và thứ tư.
● Hai đầu đoạn thẳng ở góc phần tư thứ nhất và thứ ba, có C 2 1 . C 4 1 cách.
● Hai đầu đoạn thẳng ở góc phần tư thứ hai và thứ tư, có C 3 1 . C 5 1 cách.
Suy ra số phần tử của biến cố A là
Ω A = C 2 1 . C 4 1 + C 3 1 . C 5 1 =23
Vậy xác suất cần tính
P ( A ) = Ω A Ω = 23 91
Đúng 0
Bình luận (0)
trong mặt phẳng tọa độ Oxy cho 2 điểm B(2;2), C(0;1). Tọa độ các điểm M nằm trên trục hoành thỏa MB = 2MC
\(\text{Đặt }M\left(x;y\right)\\ \overrightarrow{MB}\left(-2-x,2-y\right);\overrightarrow{MC}\left(-x,1-y\right)\\ \left|\overrightarrow{MB}\right|=\left|2\overrightarrow{MC}\right|\Leftrightarrow\sqrt{\left(-2-x\right)^2+\left(2-y\right)^2}=2\sqrt{\left(-x\right)^2+\left(1-y\right)^2}\\ \Leftrightarrow x^2+4x+4+y^2-4y+4=2x^2+2y^2-4y+2\\ \Leftrightarrow x^2+y^2-4y-6=0\\ \text{Mà }M\in Ox\Leftrightarrow y=0\Leftrightarrow x^2-6=0\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{6}\\x=-\sqrt{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}M\left(\sqrt{6};0\right)\\M\left(-\sqrt{6};0\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)