Tìm giá trị nhỏ nhất của các hàm số sau:
a) y = x3 – 3x – 4 trên nửa khoảng [−3; 2);
b) \(y=\dfrac{3x^2-4x}{x^2-1}\) trên khoảng (1; +∞).
Những câu hỏi liên quan
Tìm giá trị nhỏ nhất m của hàm số
y
x
3
+
3
x
trên khoảng
0
;
+
∞
A.
m
4
3
4
B.
m
2
3
C.
m
4
D. m...
Đọc tiếp
Tìm giá trị nhỏ nhất m của hàm số y = x 3 + 3 x trên khoảng 0 ; + ∞
A. m = 4 3 4
B. m = 2 3
C. m = 4
D. m = 2
Tìm m để giá trị lớn nhất của hàm số
y
x
3
-
3
x
+
2
m
-
1
trên đoạn
0
;
2
là nhỏ nhất. Giá trị của m thuộc khoảng? A.
0
;...
Đọc tiếp
Tìm m để giá trị lớn nhất của hàm số y = x 3 - 3 x + 2 m - 1 trên đoạn 0 ; 2 là nhỏ nhất. Giá trị của m thuộc khoảng?
A. 0 ; 1
B. - 1 ; 0
C. 2 3 ; 2
D. - 3 2 ; - 1
Tích giá trị nhỏ nhất và giá trị lớn nhất của hàm số
y
x
3
-
3
x
+
3
trên đoạn bằng A. 5. B. -75. C. -1. D. -15.
Đọc tiếp
Tích giá trị nhỏ nhất và giá trị lớn nhất của hàm số
y
=
x
3
-
3
x
+
3
trên đoạn 
bằng
A. 5.
B. -75.
C. -1.
D. -15.
Cho hàm số y x3- 3x+ 1 . Tìm tìm tập hợp tất cả giá trị m 0 , để giá trị nhỏ nhất của hàm số trên D [m+ 1; m+ 2] luôn bé hơn 3 là: A. (0; 1) B. (
1
2
; 1) C. (2; 3) D. (0; 2)
Đọc tiếp
Cho hàm số y= x3- 3x+ 1 . Tìm tìm tập hợp tất cả giá trị m> 0 , để giá trị nhỏ nhất của hàm số trên D= [m+ 1; m+ 2] luôn bé hơn 3 là:
A. (0; 1)
B. ( 1 2 ; 1)
C. (2; 3)
D. (0; 2)
+ Ta có đạo hàm : y= 3x2- 3 và y’ =0 khi và chỉ khi x= 1 hoặc x= -1 .
+ Hàm số đồng biến trên khoảng ( 1; + ∞) .
+ Trên D= [m+1; m+ 2], với m> 0 ,
ta có : M i n [ m + 1 ; m + 2 ] y = ( m + 1 ) 3 - 3 ( m + 1 ) + 1
Ycbt min y< 3 hay m3+ 3m2-4< 0
Suy ra ( m-1) (m+ 2) 2) < 0
Khi đó; m< 1 và m≠- 2
+ Kết hợp điều kiện . Suy ra: 0< m< 1.
Chọn A.
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau trên các khoảng, đoạn tương ứng: g(x) = | x 3 + 3 x 2 – 72x + 90| trên đoạn [-5; 5]
Xét hàm số f(x) = x 3 + 3 x 2 − 72x + 90 trên đoạn [-5;5]
f′(x) =3 x 2 + 6x − 72;
f′(x) = 0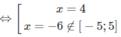 
f(−5) = 400; f(5) = −70; f(4) = −86
Ngoài ra, f(x) liên tục trên đoạn [-5;5] và f(−5).f(5) < 0 nên tồn tại x 0 ∈ (−5;5) sao cho f( x 0 ) = 0
Ta có g(x) = |f(x)| ≤ 0 và g( x 0 ) = |f( x 0 )| = 0;
g(−5) = |400| = 400
g(5) = |−70| = 70; g(4) = |f(4)| = |−86| = 86
Vậy min g(x) = g( x 0 ) = 0; max g(x) = g(−5) = 400
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
-
3
x
+
m
2
. Tổng tất cả các giá trị của tham số m sao cho giá trị nhỏ nhất của hàm số trên đoạn
-...
Đọc tiếp
Cho hàm số y = x 3 - 3 x + m 2 . Tổng tất cả các giá trị của tham số m sao cho giá trị nhỏ nhất của hàm số trên đoạn - 1 ; 1 bằng 1 là
A. 0
B. -4
C. 0
D. 4
Cho hàm số y
x
3
-
3
x
+
m
2
. Tổng tất cả các giá trị của tham số m sao cho giá trị nhỏ nhất của hàm số trên đoạn [-1;1] bằng 1 là A. 1 B. -4 C. 0 D. 4
Đọc tiếp
Cho hàm số y = x 3 - 3 x + m 2 . Tổng tất cả các giá trị của tham số m sao cho giá trị nhỏ nhất của hàm số trên đoạn [-1;1] bằng 1 là
A. 1
B. -4
C. 0
D. 4
Chọn C
Xét hàm số f(x) = x 3 - 3 x + m .
Để GTNN của hàm số y =
x
3
-
3
x
+
m
2
trên đoạn [-1;1] bằng 1 thì 
hoặc 
Ta có 
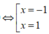
=> f(x) nghịch biến trên [-1;1]
Suy ra 
và 
Trường hợp 1: 
Trường hợp 2: 
Vậy tổng các giá trị của tham số m là 0.
Đúng 0
Bình luận (0)
Hàm số
y
(
x
+
m
)
3
+
(
x
+
n
)
3
-
x
3
đồng biến trên khoảng
(...
Đọc tiếp
Hàm số y = ( x + m ) 3 + ( x + n ) 3 - x 3 đồng biến trên khoảng ( - ∞ ; + ∞ ) . Giá trị nhỏ nhất của biểu thức P = 4 ( m 2 + n 2 ) - m - n bằng
A. - 16
B. 4
C. - 1 16
D. 1 4
Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x 3 - 2 x 2 + 3 x - 4 trên đoạn [1;3] Khi đó, giá trị M-m bằng:
A. 12
B. 14
C. 2
D. 16
Giá trị nhỏ nhất của hàm số
y
x
2
+
2
x
+
5
trên nửa khoảng [-4;
+
∞
) là A.
m
i
n
[
-
4
;
+
∞
)
y
5
B.
m...
Đọc tiếp
Giá trị nhỏ nhất của hàm số y = x 2 + 2 x + 5 trên nửa khoảng [-4; + ∞ ) là
A. m i n [ - 4 ; + ∞ ) y = 5
B. m i n [ - 4 ; + ∞ ) y = - 17
C. m i n [ - 4 ; + ∞ ) y = 4
D. m i n [ - 4 ; + ∞ ) y = - 9
