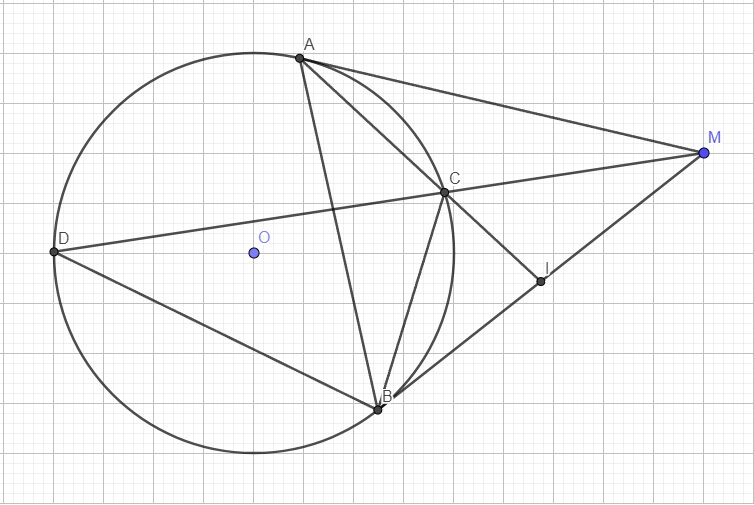
Từ một điểm M nằm ngoài (O;R) với OM > 2R. Vẽ hai tiếp tuyến MA, MB với (O). Gọi I là trung điểm của AM, BI cắt (O) tại C, tia MC cắt (O) tại D.a) Chứng minh OM vuông góc AB tại H và IA^2 = IB.IC.b) Chứng minh BD // AMc) Chứng minh tứ giác AHCI nội tiếp và CA là tia phân giác của góc ICD.d) AO cắt BD tại K. Chứng minh ba đường thẳng MD, AB và IK đồng quy tại một điểm.

Những câu hỏi liên quan
Trên một đường thẳng lấy ba điểm M, N, O trong đó O nằm giữa M và N. Từ điểm A nằm ngoài đường thẳng này vẽ các tia AM, AN, AO. Lấy điểm B nằm giữa O và A. Tia MB cắt tia AN tại C. Giải thích vì sao điểm C nằm giữa A và N.
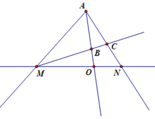
Tia MB cắt đoạn thẳng AO tại điểm B nằm giữa A và O nên tia MB nằm giữa hai tia MA, MO (hay tia MB nằm giữa hai tia MA, MN).
Vì tia MB nằm giữa hai tia MA, MN nên tia MB cắt đoạn thẳng AN tại điểm C nằm giữa hai điểm A, N.
Vậy tia MB cắt tia AN tại điểm C nằm giữa A, N.
Đúng 0
Bình luận (0)
Cho đường tròn (O; R) và một điểm M nằm ngoài đường tròn. Từ M kẻ các tiếp tuyến MB,MC tới (O) (B, C là các tiếp điểm). Gọi H là giao điểm của MO với BC. Vẽ đường kính BA.a) Chứng minh: Các điểm M, B, C, O cùng nằm trên một đường tròn.b) Chứng minh: CH* OH.HM.
Đọc tiếp
Cho đường tròn (O; R) và một điểm M nằm ngoài đường tròn. Từ M kẻ các tiếp tuyến MB,
MC tới (O) (B, C là các tiếp điểm). Gọi H là giao điểm của MO với BC. Vẽ đường kính BA.
a) Chứng minh: Các điểm M, B, C, O cùng nằm trên một đường tròn.
b) Chứng minh: CH* = OH.HM.
a: Xét tứ giác MBOC có \(\widehat{MBO}+\widehat{MCO}=90^0+90^0=180^0\)
=>MBOC là tứ giác nội tiếp
=>M,B,O,C cùng thuộc một đường tròn
b: Sửa đề: \(CH\cdot HB=OH\cdot HM\)
Xét (O) có
MB,MC là các tiếp tuyến
Do đó: MB=MC
=>M nằm trên đường trung trực của BC(1)
ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra MO là đường trung trực của BC
=>MO\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOBM vuông tại B có BH là đường cao
nên \(OH\cdot HM=HB^2\)
=>\(OH\cdot HM=HB\cdot HC\)
Đúng 1
Bình luận (0)
Cho đường tròn (O; R) và một điểm M cố định nằm ngoài đường tròn (O). Từ M kẻ các tiếp tuyến MA, MB tới (O) (A, B là các tiếp điểm). MO cắt AB tại H. Một đường thẳng d thay đổi đi qua M nhưng không đi qua O cắt đường tròn (O) tại hai điểm N, P (N nằm giữa M và P). Gọi I là trung điểm của NP.a) Chứng minh bốn điểm M, A, I, O cùng thuộc một đường tròn.b) Qua B kẻ đường thẳng song song với MO và cắt đường tròn (O) tại D. Chứng minh và AD là đường kính của (O).c) Tiếp tuyến của (O) tại N và P cắt...
Đọc tiếp
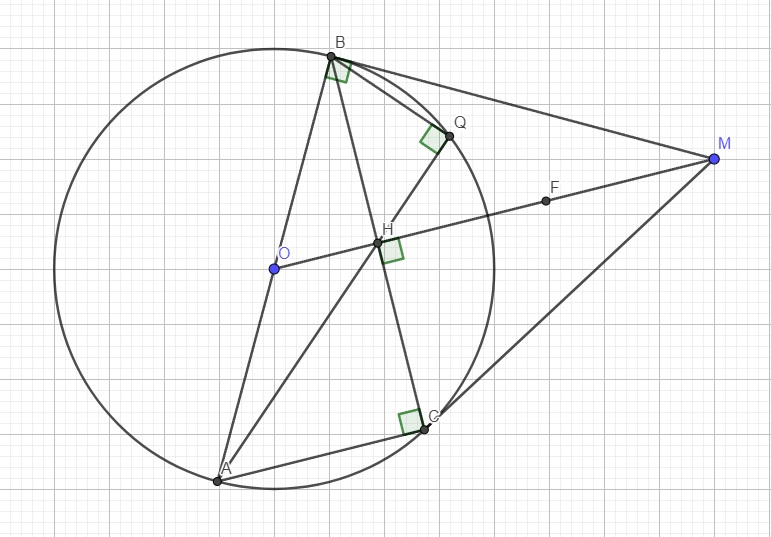
Cho đường tròn (O; R) và một điểm M cố định nằm ngoài đường tròn (O). Từ M kẻ các tiếp tuyến MA, MB tới (O) (A, B là các tiếp điểm). MO cắt AB tại H. Một đường thẳng d thay đổi đi qua M nhưng không đi qua O cắt đường tròn (O) tại hai điểm N, P (N nằm giữa M và P). Gọi I là trung điểm của NP.
a) Chứng minh bốn điểm M, A, I, O cùng thuộc một đường tròn.
b) Qua B kẻ đường thẳng song song với MO và cắt đường tròn (O) tại D. Chứng minh ![]() và AD là đường kính của (O).
và AD là đường kính của (O).
c) Tiếp tuyến của (O) tại N và P cắt nhau tại F. Chứng minh ![]() đồng dạng
đồng dạng ![]() và điểm F chuyển động trên một đường thẳng cố định khi đường thẳng d quay quanh M mà vẫn thỏa mãn các yêu cầu đề bài.
và điểm F chuyển động trên một đường thẳng cố định khi đường thẳng d quay quanh M mà vẫn thỏa mãn các yêu cầu đề bài.
Câu a),b) tự làm nhé , mình chỉ giúp câu c) thôi .
OI vuông góc NP ( Do I là trung điểm của MP ) , OF vuông góc NP ( Do OF là đường trung trực của NP )
=> O,I,F thẳng hàng
Tam giác ONF vuông tại N , đường cao NI
=> ON^2 = OI.OF
Mà ON=OA
OA^2 = OH.OM
=> OH.OM=OI.OF
=> OH/OI=OF/OM
Xét tam giác OIM và tam giác OHF có
góc MOF chung
OH/OI=OF/OM
=> Tam giác OIM đồng dạng tam giác OHF
=> góc OHF=góc OIM (=90 độ )
OH vuông HF
mà OH vuông AB
=> A,B,F thẳng hàng
=> F nằm trên đường thẳng cố định AB khi đường thẳng d quay quanh M mà vẫn thỏa mãn các yêu cầu đề bài
Điều phải chứng minh
Đúng 0
Bình luận (0)
TỪ một điểm M nằm ngoài đường tròn kẻ tiếp tuyến MA MB nằm ngoài đường tròn . Lấy điểm E nằm ngoài đường trong sao cho AE>EB . Kẻ đường thẳng vuông góc với OE tại E cắt MA ơn C cắt MB kẻ Đ a, chứng mình C A E O thuộc dường tròn b, E là trung điểm của CD
Xem chi tiết
Trên một đường thẳng lấy ba điểm M, N, O trong đó O nằm giữa M và N. Từ điểm A nằm ngoài đường thẳng này vẽ các tia AM, AN, AO. Trong các tia AM, AN, AO, tia nào nằm giữa hai tia còn lại, tia nào không nằm giữa hai tia còn lại?
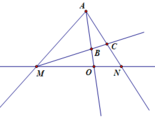
Tia AO cắt đoạn thẳng MN tại điểm O nằm giữa hai điểm M và N. Do đó tia AO nằm giữa hai tia AM, AN.
Tia AM không cắt đoạn thẳng ON nên tia AM không nằm giữa hai tia AO và AN. Tương tự, tia AN không nằm giữa hai tia AM, AO.
Đúng 0
Bình luận (0)
Từ điểm M nằm ngoài (O) vẽ hai tiếp tuyến MA, MB (A,B là tiếp điểm) a) Chứng minh 4 điểm M,A,O,B cùng thuộc một đường tròn b) Vẽ I là trung điểm MB. Nối AI cắt (O) tại C. Chứng minh IB²=IC.IA c) MC cắt (O) tại D. Chứng minh MB²= MC.MD Suy ra MC.MD=IC.IA
a: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
b: Xét (O) có
\(\widehat{IBC}\) là góc tạo bởi tiếp tuyến BI và dây cung BC
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{IBC}=\widehat{BAC}\)
Xét ΔIBC và ΔIAB có
\(\widehat{IBC}=\widehat{IAB}\)
\(\widehat{BIC}\) chung
Do đó: ΔIBC~ΔIAB
=>\(\dfrac{IB}{IA}=\dfrac{IC}{IB}\)
=>\(IB^2=IA\cdot IC\)
c: Xét (O) có
\(\widehat{MBC}\) là góc tạo bởi tiếp tuyến BM và dây cung BC
\(\widehat{CDB}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{MBC}=\widehat{CDB}\)
Xét ΔMBC và ΔMDB có
\(\widehat{MBC}=\widehat{MDB}\)
\(\widehat{BMC}\) chung
Do đó: ΔMBC~ΔMDB
=>\(\dfrac{MB}{MD}=\dfrac{MC}{MB}\)
=>\(MB^2=MD\cdot MC\)
Đúng 2
Bình luận (0)
a. Em tự giải
b.
Ta có: IB là tiếp tuyến (O) tại B nên \(\widehat{BAC}=\widehat{CBI}\) (góc nội tiếp và góc tạo bởi tiếp tuyến - dây cung cùng chắn BC)
Xét hai tam giác ABI và BCI có:
\(\left\{{}\begin{matrix}\widehat{BAC}=\widehat{CBI}\left(cmt\right)\\\widehat{BIA}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta ABI\sim\Delta BCI\left(g.g\right)\)
\(\Rightarrow\dfrac{IA}{IB}=\dfrac{IB}{IC}\Rightarrow IB^2=IC.IA\)
c.
Ta có \(\widehat{BDC}\) và \(\widehat{MBC}\) là góc nội tiếp và góc tạo bởi tiếp tuyến sây cung cùng chắn BC
\(\Rightarrow\widehat{BDC}=\widehat{MBC}\)
Xét hai tam giác MBD và MCB có:
\(\left\{{}\begin{matrix}\widehat{BMD}\text{ chung}\\\widehat{BDC}=\widehat{MBC}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta MBD\sim\Delta MCB\left(g.g\right)\)
\(\Rightarrow\dfrac{MB}{MC}=\dfrac{MD}{MB}\Rightarrow MB^2=MC.MD\)
Đẳng thức cuối em ghi sai.
Do I là trung điểm MB \(\Rightarrow MB=2IB\Rightarrow MB^2=4IB^2\)
\(\Rightarrow MC.MD=4IC.IA\) (đây mới là đẳng thức đúng)
Đúng 3
Bình luận (0)
Cho đường tròn (O) và điểm M nằm ngoài (O). Từ M kẻ hai tiếp tuyến MA, MB đển (O) (A, B là các tiếp điểm). Qua M kẻ cát tuyên MNP (MN MP) đến (O). Gọi K là trung điểm của NPa, Cho đường tròn (O) và điểm M nằm ngoài (O). Từ M kẻ haib, Chứng minh tia KM là phân giác của góc
A
K
B
^
c, Gọi Q là giao điểm thứ hai của BK với (O). Chứng minh AQ song song NPd, Gọi H là giao điểm của AB...
Đọc tiếp
Cho đường tròn (O) và điểm M nằm ngoài (O). Từ M kẻ hai tiếp tuyến MA, MB đển (O) (A, B là các tiếp điểm). Qua M kẻ cát tuyên MNP (MN < MP) đến (O). Gọi K là trung điểm của NP
a, Cho đường tròn (O) và điểm M nằm ngoài (O). Từ M kẻ hai
b, Chứng minh tia KM là phân giác của góc A K B ^
c, Gọi Q là giao điểm thứ hai của BK với (O). Chứng minh AQ song song NP
d, Gọi H là giao điểm của AB và MO. Chứng minh: MA2 = MH.MO = MN.MP
e, Chứng minh bốn điểm N, H, O, P cùng thuộc một đường tròn
cho đường tròn tâm o bán kính và m là một điểm nằm bên ngoài đường tròn . từ m kẻ hai tiếp tuyến từ ma,mb với đường tròn r (o) (a b là các tiếp điểm gọi e là giao điểm của ab và om
cho đường tròn tâm o bán kính và m là một điểm nằm bên ngoài đường tròn . từ m kẻ hai tiếp tuyến từ ma,mb với đường tròn r (o) (a b là các tiếp điểm gọi e là giao điểm của ab và om
Cho đường tròn (O;R) và một điểm M nằm ngoài đường tròn. Từ M kẻ các tiếp tuyến MB,MC tới (O) (B,C là tiếp điểm). Gọi H là giao điểm của MO với BC. Vẽ đường kính BA. a) Cm các điểm M,B,O,C cùng nằm trên 1 đg tròn b) Cm: CH^2OH.HM c) Gọi F là trung điểm của MH,AH cắt (O) tại giao điểm...
Đọc tiếp
Cho đường tròn (O;R) và một điểm M nằm ngoài đường tròn. Từ M kẻ các tiếp tuyến MB,MC tới (O) (B,C là tiếp điểm). Gọi H là giao điểm của MO với BC. Vẽ đường kính BA. a) Cm các điểm M,B,O,C cùng nằm trên 1 đg tròn b) Cm: CH^2=OH.HM c) Gọi F là trung điểm của MH,AH cắt (O) tại giao điểm thứ hai là Q.Cm tam giác MBH đồng dạng tam giác BAC và B,Q,F thẳng hàng
a. Câu này đơn giản em tự giải.
b.
Ta có: \(\left\{{}\begin{matrix}OB=OC=R\\MB=MC\left(\text{t/c hai tiếp tuyến cắt nhau}\right)\end{matrix}\right.\)
\(\Rightarrow OM\) là trung trực của BC
\(\Rightarrow OM\perp BC\) tại H đồng thời H là trung điểm BC hay \(HB=HC\)
\(OC\perp MC\) (MC là tiếp tuyến tại C) \(\Rightarrow\Delta OMC\) vuông tại C
Áp dụng hệ thức lượng trong tam giác vuông OMC với đường cao CH:
\(CH^2=OH.MH\)
c.
C nằm trên đường tròn và AB là đường kính \(\Rightarrow\widehat{ACB}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{ACB}=90^0\)
Xét hai tam giác MBH và BAC có:
\(\left\{{}\begin{matrix}\widehat{MHB}=\widehat{ACB}=90^0\\\widehat{MBH}=\widehat{BAC}\left(\text{cùng chắn BC}\right)\end{matrix}\right.\) \(\Rightarrow\Delta MBH\sim\Delta BAC\left(g.g\right)\)
\(\Rightarrow\dfrac{BH}{AC}=\dfrac{MH}{BC}\Rightarrow\dfrac{BH}{AC}=\dfrac{2HF}{2CH}\) (do F là trung điểm MH và H là trung điểm BC)
\(\Rightarrow\dfrac{BH}{AC}=\dfrac{HF}{CH}\)
Xét hai tam giác BHF và ACH có:
\(\left\{{}\begin{matrix}\dfrac{BH}{AC}=\dfrac{HF}{CH}\left(cmt\right)\\\widehat{BHF}=\widehat{ACH}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta BHF\sim\Delta ACH\left(c.g.c\right)\)
\(\Rightarrow\widehat{HBF}=\widehat{CAH}\)
Mà \(\widehat{CAH}=\widehat{CBQ}\) (cùng chắn CQ)
\(\Rightarrow\widehat{HBF}=\widehat{CBQ}\) hay \(\widehat{HBF}=\widehat{HBQ}\)
\(\Rightarrow B,Q,F\) thẳng hàng
Đúng 2
Bình luận (0)