Cho tam giác ABC, BC = 4cm. Gọi D, E theo thứ tự là trung điểm của AC, AB ; M, N theo thứ tự là trung điểm của BE, CD. MN cắt BD tại P, MN cắt CE tại Q.
a. Tính độ dài đoạn MN
b. Chứng minh rằng MP = PQ = QN
Cho tam giác nhọn ABC (AC > AB), đường cao AH. Gọi D, E, F theo thứ tự là trung điểm của AB, AC, BC. Biết AH = 8cm, HB = 4cm, HC = 6cm, tính diện tích các tứ giác DECH, BDEF và DEFH.
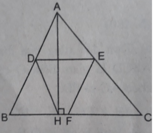
S D E C H = 22 c m 2 ; S B D E F = 20 c m 2 ; S D E F H = 12 c m 2
cho tam giác ABC : BC = 4cm . Gọi D,E theo thứ tự là trung điểm của AC , AB , M và N theo thứ tự là trung điểm của BE , CD . MN cắt BD ở H , cắt CE ở K
a) tính MN
b) MH= HK = KN
Cho tam giác cân ABC (AB=AC) .Gọi D là trung điểm của BC, từ D hạ DE, DF vuông góc với Á theo thứ tự AC. Chứng minh:
a) tam giác AED = tam giác ÀD vuông góc vơi AB, AC theo thứ tự (E thuôc AB, F thuộc AC). Chứng minh:
a) tam giác AED= tam giác AFD và AD là trung trực của đoạn thẳng EF
b) Trên tia đối tia DE lấy điểm K sao cho DK=DE. Chứng minh tam giác EKC vuông
c) So sánh BF và EK
a: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
góc EAD=góc FAD
=>ΔAED=ΔAFD
=>AE=AF và DE=DF
=>AD là trung trực của EF
b: Sửa đề: ΔEKF
Xét ΔEKF có
FD là trung tuyến
FD=EK/2
=>ΔFEK vuông tại F
Cho tam giác nhọn ABC (AC > AB), đường cao AH. Gọi D, E, F theo thứ tự là trung điểm của AB, AC, BC. Tính độ dài HE.
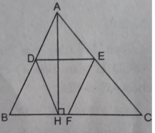
A C 2 = A H 2 + H C 2 = 8 2 + 6 2 = 10 2 ⇒ AC = 10cm;
HE = 1/2 AC = 1/2.10 = 5 (cm).
Cho tam giác ABC có BC=4cm. Gọi D,E lần lượt là trung điểm AC, AB; M,N theo thứ tự là trung điểm BE và CD. MN cắt BD ở P, cắt CE ở Q
Cm MP=PQ=QN
Bài 4: Cho tứ giác ABCD(AB//CD). Gọi E;F;K theo thứ tự là trung điểm của AD;BC;AC.
1) So sánh các độ dài của tam giác MIK
2) Chứng minh EF=AB+CD/2
Bài 5: Cho tam giác ABC có D là trung điểm của AB.Tia Dz//BC cắt AC tại E. chứng minh E là trung điểm của AC
Bài 5:
Xét ΔABC có
D là trung điểm của AB
DE//BC
Do đó: E là trung điểm của AC
Bài 4:
2: Xét hình thang ABCD có
E,F lần lượt là trung điểm của AD,BC
=>EF là đường trung bình của hình thang ABCD
=>EF//AB//CD và \(EF=\dfrac{AB+CD}{2}\)
Cho tam giác ABC có BC =4cm , gọi DE theo thứ tự là trung điểm của AC,AB,M,N theo thứ tự là trung điểm của BE và CD , MN cắt BD ở P ,cắt CE ở Q.Chứng minh: a. Tam giác MAD là tam giác cân b. MP=PQ=QP
Cho tam giác ABC có BC= 4cm gọi D,E theo thứ tự là trung điểm AC,AB
GỌi M là trung điểm BC qua E và M lần lượt kẻ các đường thẳng song song với BD cắt AC tại F và N. CM EF=MN
Ai nhanh và đúng mk tick nha
Ta có xet tam giác CDB có
CM= MB ( m t điểm cb )
NM //BD
=> CN= CD
Lại có CM=MB và CN =CD => NM là đường tb tg CDB
=> NM=1/2 BD (2)
Xét tg ADB
AE=EB
FE//BD
=> AF=FD
Lại có AF=FD và AE=EB => FE là đường tb tg ADB
=> EF= 1/2 BD (1)
Từ 1,2 => Ef = MN
Cho tam giác ABC cân tại A. Gọi D, E, F theo thứ tự là trung điểm của AB, BC, AC. Tam giác ABC có thêm điều kiện gì thì ADEF là hình vuông ?
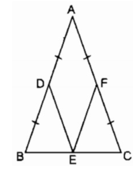
Hình thoi ADEF là hình vuông ⇒ ∠ A = 90 0
⇒ ∆ ABC vuông cân tại A
Ngược lại nếu ∆ ABC vuông cân tại A
⇒ Tứ giác ADEF là hình thoi có ∠ A = 90 0
⇒ Hình thoi ADEF là hình vuông
Vậy hình thoi ADEF là hình vuông thì ∆ ABC vuông cân tại A.