Cho ABC có AB = 3 cm; AC = 4 cm; BC = 5 cm.
a) Chứng tỏ tam giác ABC vuông tại A.
b)Vẽ phân giác BD (D thuộc AC), từ D vẽ DE ^ BC (E thuộc BC). Chứng minh DA = DE.
Những câu hỏi liên quan
Cho tam giác ABC có AB = 3 cm, AC = 4 cm, BC = 5 cm. Chứng minh B A C ^ = 90 ° .
Cho Δ ABC vuông tại A có cạnh AB = 3 cm;AC = 4 cm. Tính diện tích của tam giác Δ ABC ?
Cho hình tam giác ABC có AB = 3,2 cm,HM vuông góc với AB và HM = 1,3 cm,đoạn thẳng BH = 1/3 cạnh BC.Tính diện tích hình ABC
Cho tam giác ABC có AB = 3 cm; AC = 4 cm; BC=5cm. Chứng tỏ tam giác ABC vuông tại A
Ta có : 3^2+4^2=9+16=25
Căn bậc hai của 25 bằng 5 suy ra tam giac ABC vuong tai A
Đúng 0
Bình luận (0)
ta có:
\(AB^2+AC^2=3^2+4^2=9+16=25\)
\(BC^2=5^2=25\)
=> tam giác ABC vuông tại A
Đúng 0
Bình luận (0)
cho hình tam giác ABC có AB = 3,2 cm . Lấy H trên BC biết BH = 1/3 BC . HM vuông góc với AB , HM = 1,3 cm . Tính diện tích ABC
Diện tích tam giác ABH là:
3,2×1,3:2=2,083,2×1,3:2=2,08 (cm2cm2 )
Vì đoạn thẳng BH bằng 1313 BC nên diện tích tam giác ABH bằng 1313 diện tích tam giác ABC
Diện tích tam giác ABC là:
2,08×3=6,242,08×3=6,24 (cm2cm2 )
Đáp số: 6,246,24 cm2
Bài 3 (3,0 điểm). Cho ABC có AB cm AC cm BC cm 9 , 12 , 15 .a) Chứng minh ABC vuông và so sánh các góc của ABC ;b) Trên tia đối của tia AB lấy điểm D sao cho AB AD. Chứng minh DBC cân;c) Gọi K là trung điểm của cạnh BC. Đường thẳng DK cắt cạnh AC tại M. Tính CM;d) Từ trung điểm N của đoạn thẳng AC kẻ đường thẳng vuông góc với AC cắt DC tại I. Chứngminh ba điểm B, M, I thẳng hàng.Bài 3 (3,0 điểm). Cho ABC có AB cm AC cm BC cm 9 , 12 , 15 .a) Chứng minh ABC vuông và so sán...
Đọc tiếp
Bài 3 (3,0 điểm). Cho ABC có AB cm AC cm BC cm 9 , 12 , 15 .
a) Chứng minh ABC vuông và so sánh các góc của ABC ;
b) Trên tia đối của tia AB lấy điểm D sao cho AB = AD. Chứng minh DBC cân;
c) Gọi K là trung điểm của cạnh BC. Đường thẳng DK cắt cạnh AC tại M. Tính CM;
d) Từ trung điểm N của đoạn thẳng AC kẻ đường thẳng vuông góc với AC cắt DC tại I. Chứng
minh ba điểm B, M, I thẳng hàng.
Bài 3 (3,0 điểm). Cho ABC có AB cm AC cm BC cm 9 , 12 , 15 .
a) Chứng minh ABC vuông và so sánh các góc của ABC ;
b) Trên tia đối của tia AB lấy điểm D sao cho AB = AD. Chứng minh DBC cân;
c) Gọi K là trung điểm của cạnh BC. Đường thẳng DK cắt cạnh AC tại M. Tính CM;
d) Từ trung điểm N của đoạn thẳng AC kẻ đường thẳng vuông góc với AC cắt DC tại I. Chứng
minh ba điểm B, M, I thẳng hàng.
làm hộ mik ý D với
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔACB vuông tại A
b: Xét ΔCDB có
CA là đường cao
CA là đường trung tuyến
Do đó;ΔCDB cân tại C
c: Xét ΔCAB có
CA là đường trung tuyến
DK là đường trung tuyến
CA cắt DK tại M
Do đó: M là trọng tâm của ΔCBA
Suy ra: CM=2/3CA=2/3x12=8(cm)
Đúng 0
Bình luận (0)
Bạn Thảo cho rằng tam giác ABC trong Hình 21 có \(AB = 3\)cm, \(BC = 2\)cm, \(AC = 4\)cm.
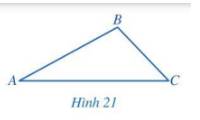
a) Bạn Thảo nói đúng.
b) \(AB + BC = 3 + 2 = 5 > AC = 4\).
Vậy \(AB + BC\) > AC.
Đúng 0
Bình luận (0)
17 tháng 5 2016 lúc 20:51
Cho tam giác vuông ABC có AB = 3 cm , AC = 4 cm . Tính BC
Áp dụng định lý Py-ta-go vào tam giác vuông ABC vuông tại A ;ta có
AB^2+AC^2=BC^2
Hay: 3^2+4^2=BC^2
BC^2=9+16=25
Suy ra BC= căn bậc 2 của 25=5 cm
Vậy BC=5 cm
Đúng 0
Bình luận (0)
Ap dụng định lí Py-ta-go trong \(\Delta_vABC\) có :
\(AB^2+AC^2\)
\(AB^2=3^2+4^2\)
\(AB^2=9+16\)
\(AB^2=25\)
\(AB=\sqrt{25}\)
\(AB=5cm\)
Đúng 0
Bình luận (0)
-Nếu tam giác ABC vuông tại A
Theo định lý Py-ta-go ta có: AB2+AC2=BC2 =>BC=5 (cm)
-Nếu tam giác ABC vuông tại B
Theo định lý Py-ta-go ta có: AB2+BC2=AC2 =>BC=\(\sqrt{7}\left(cm\right)\)
-Nếu tam giác ABC vuông tại C
Theo định lý Py-ta-go ta có: BC2+AC2=AB2 =>BC=\(-\sqrt{7}\left(cm\right)\)(vô lí)
\(KL:BC=\left\{\sqrt{7};5\right\}\)(cm)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho Δ ABC vuông tại A có AB = 3 cm, BC = 5 cm, AD là đường phân giác của Δ ABC. Chọn phát biểu đúng?
A. BD = 20/7 cm; CD = 15/7 cm
B. BD = 15/7 cm; CD = 20/7 cm
C. BD = 1,5 cm; CD = 2,5 cm
D. BD = 2,5 cm; CD = 1,5 cm
Áp dụng định lý Py – ta – go ta có: A C = ( B C 2 - A B 2 ) = ( 52 - 32 ) = 4 ( c m )
Δ ABC, AD là đường phân giác của góc BACˆ ( D ∈ BC )
Ta có: DB/DC = AB/AC hay DB/AB = DC/AC
Khi đó ta có: DB/DC = AB/AC ⇒ DB/( DB + DC ) = AB /( AB + AC )
hay DB/5 = 3/( 3 + 4) ⇒ DB = 15/7 cm; DC = 20/7 ( cm )
Chọn đáp án B.
Đúng 0
Bình luận (0)
Cho Δ ABC vuông tại A có AB = 3 cm, BC = 5 cm, AD là đường phân giác của Δ ABC. Chọn phát biểu đúng?
A. BD = 20/7 cm; CD = 15/7 cm
B. BD = 15/7 cm; CD = 20/7 cm
C. BD = 1,5 cm; CD = 2,5 cm
D. BD = 2,5 cm; CD = 1,5 cm
Áp dụng định lý Py – ta – go ta có: A C = ( B C 2 - A B 2 ) = ( 5 2 - 3 2 ) = 4 ( c m )
Δ ABC, AD là đường phân giác của góc BACˆ ( D ∈ BC )
Ta có: DB/DC = AB/AC hay DB/AB = DC/AC
Khi đó ta có: DB/DC = AB/AC ⇒ DB/(DB + DC) = AB/(AB + AC)
hay DB/5 = 3/(3 + 4) ⇒ DB = 15/7 cm; DC = 20/7 ( cm )
Chọn đáp án B.
Đúng 0
Bình luận (0)