cho A và B là hai điểm trên đường tròn (O;3cm) sao cho góc AOB = 120. Tính số đo và độ dài các cung có hai mút AB

Những câu hỏi liên quan
Cho đường tròn tâm O điểm A nằm ngoài đường tròn. Vẽhai tiếp tuyến AM, AN với đường tròn tâm O ( M,N là hai tiếp điểm). Qua A vẽ 1 đường thẳng d cắt đường tròn tâm O tại B và C sao cho 2 điểm nằm giữa A và C, hai điểm O và N nằm trên hai nửa mặt phẳng đối nhau bên bờ là đường thẳng d. Đường thẳng MN cắt AO và AC lần lượt tại H và K.
a, Chứng minhAM bình AH.AO
b, Gọi I là trung điểm của BC. Chứng minh góc AMK góc AIN
c, Chứng minh rằng đường tròn ngoại tiếp tam giác OHK lun đi qua 1 điểm cố định...
Đọc tiếp
Cho đường tròn tâm O điểm A nằm ngoài đường tròn. Vẽhai tiếp tuyến AM, AN với đường tròn tâm O ( M,N là hai tiếp điểm). Qua A vẽ 1 đường thẳng d cắt đường tròn tâm O tại B và C sao cho 2 điểm nằm giữa A và C, hai điểm O và N nằm trên hai nửa mặt phẳng đối nhau bên bờ là đường thẳng d. Đường thẳng MN cắt AO và AC lần lượt tại H và K.
a, Chứng minhAM bình = AH.AO
b, Gọi I là trung điểm của BC. Chứng minh góc AMK= góc AIN
c, Chứng minh rằng đường tròn ngoại tiếp tam giác OHK lun đi qua 1 điểm cố định khi đường tròn tâm O thay đổi nhưng lun đi qua điểm B và C cố định
Cho hai đường tròn (O) và (O) có cùng bán kính R cắt nhau tại hai điểm A, B sao cho tâm O nằm trên đường tròn (O) và tâm O nằm trên đường tròn (O). Đường nối tâm OO cắt AB tại H, cắt đường tròn (O) tại giao điểm thứ hai là C. Gọi F là điểm đối xứng của B qua O.a) Chứng minh rằng AC là tiếp tuyến của (O), và AC vuông góc BF.b) Trên cạnh AC lấy điểm D sao cho AD AF. Qua D kẽ đường thăng vuông góc với OC cắt OC tại K, Cắt AF tại G. Gọi E là giao điểm của AC và BF. Chứng minh các tứ giác AHOE, ADKO...
Đọc tiếp
Cho hai đường tròn (O) và (O') có cùng bán kính R cắt nhau tại hai điểm A, B sao cho tâm O nằm trên đường tròn (O') và tâm O' nằm trên đường tròn (O). Đường nối tâm OO' cắt AB tại H, cắt đường tròn (O') tại giao điểm thứ hai là C. Gọi F là điểm đối xứng của B qua O'.
a) Chứng minh rằng AC là tiếp tuyến của (O), và AC vuông góc BF.
b) Trên cạnh AC lấy điểm D sao cho AD = AF. Qua D kẽ đường thăng vuông góc với OC cắt OC tại K, Cắt AF tại G. Gọi E là giao điểm của AC và BF. Chứng minh các tứ giác AHO'E, ADKO là các tứ giác nội tiếp.
c) Tứ giác AHKG là hình gì? Vì sao.
d) Tính diện tích phần chung của hình (O) và hình tròn (O') theo bán kính R.
Cho đường tròn (O ; r) và đường thẳng d không cắt đường tròn .từ điểm M trên đường thẳng (d) vẽ hai tiếp tuyến MA MB với đường tròn (O)( A,B là hai tiếp điểm). Gọi H là giao điểm của mo và AB kẻ đường kính AC Chứng minh rằng:bốn điểm m A,O,B cùng thuộc một đường trònb.BC song song với MOC Đường thảng vuông góc với AC tại O cắt AB tại y.Chứng minh rằng HI.HB+HO.HMR2d. KHI ĐIỂM m di chuyển trên đường thẳng(d) thì đường thẳng AB luôn đi qua 1 điểm cố định
Đọc tiếp
Cho đường tròn (O ; r) và đường thẳng d không cắt đường tròn .từ điểm M trên đường thẳng (d) vẽ hai tiếp tuyến MA MB với đường tròn (O)( A,B là hai tiếp điểm). Gọi H là giao điểm của mo và AB kẻ đường kính AC Chứng minh rằng:
bốn điểm m A,O,B cùng thuộc một đường tròn
b.BC song song với MO
C Đường thảng vuông góc với AC tại O cắt AB tại y.Chứng minh rằng HI.HB+HO.HM=R2
d. KHI ĐIỂM m di chuyển trên đường thẳng(d) thì đường thẳng AB luôn đi qua 1 điểm cố định
a: Xét tứ giác OAMB có \(\widehat{OAM}+\widehat{OBM}=90^0+90^0=180^0\)
nên OAMB là tứ giác nội tiếp
=>O,A,M,B cùng thuộc 1 đường tròn
b: Xét (O) có
MA,MB là tiếp tuyến
Do đó: MA=MB
mà OA=OB
nên MO là đường trung trực của AB
=>MO\(\perp\)AB tại H và H là trung điểm của AB
Xét (O) có
ΔABC nội tiếp
AC là đường kính
Do đó: ΔABC vuông tại B
=>BA\(\perp\)BC
mà AB\(\perp\)OM
nên BC//OM
c: Sửa đề: cắt AB tại I
Xét ΔAOI vuông tại O có OH là đường cao
nên \(HA\cdot HI=OH^2\)
=>\(HB\cdot HI=OH^2\)
Xét ΔOAM vuông tại A có AH là đường cao
nên \(HO\cdot HM=HA^2\)
Xét ΔOHA vuông tại H có \(OA^2=OH^2+HA^2\)
=>\(R^2=HB\cdot HI+HO\cdot HM\)
Đúng 1
Bình luận (0)
Cho đường tròn (O,5) và a là điểm cố định trên đường tròn Gọi B C D là hai điểm di động trên đường tròn sao cho đoạn BC có độ dài không đổi bằng 8. gọi M là trung điểm của BC và G là trọng tâm tam giác ABC. khi B,C thay đổi trên đường tròn (O,5) thì tập hợp các điểm G là:
A. đường tròn có bán kính bằng 3
B. đường tròn có bán kính bằng 2
C. đường tròn có bán kính bằng 4
D. đường tròn có bán kính bằng 5
em đang cần gấp. cảm ơn ạ
Đọc tiếp
Cho đường tròn (O,5) và a là điểm cố định trên đường tròn Gọi B C D là hai điểm di động trên đường tròn sao cho đoạn BC có độ dài không đổi bằng 8. gọi M là trung điểm của BC và G là trọng tâm tam giác ABC. khi B,C thay đổi trên đường tròn (O,5) thì tập hợp các điểm G là:
A. đường tròn có bán kính bằng 3
B. đường tròn có bán kính bằng 2
C. đường tròn có bán kính bằng 4
D. đường tròn có bán kính bằng 5
em đang cần gấp. cảm ơn ạ
Theo t/c đường tròn, do M là trung điểm BC \(\Rightarrow OM\perp BC\)
Áp dụng định lý Pitago:
\(OM=\sqrt{OC^2-CM^2}=\sqrt{R^2-\left(\dfrac{BC}{2}\right)^2}=3\)
\(\Rightarrow\) Quỹ tích M là đường tròn tâm \(\left(O;3\right)\)
Mặt khác do G là trọng tâm tam giác ABC
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)
\(\Rightarrow\) G là ảnh của M qua phép vị tự tâm A tỉ số \(k=\dfrac{2}{3}\)
\(\Rightarrow\) Quỹ tích G là ảnh của \(\left(O;3\right)\) qua phép vị tự tâm A tỉ số \(k=\dfrac{2}{3}\)
\(\Rightarrow\) Quỹ tích G là đường tròn bán kính \(\dfrac{2}{3}.3=2\)
Đúng 0
Bình luận (0)
Cho đường tròn tâm O, đường kính AB và d là một tiếp tuyến của đường tròn (O) tại điểm A. Trên đường thẳng d lấy điểm M (khác A) và trên đoạn OB lấy điểm N (khác O và B). Đường thẳng MN cắt đường tròn (O) tại hai điểm C và D sao cho C nằm giữa M và D. Gọi H là trung điểm của đoạn thẳng CD.a) Chứng minh tứ giác AOHM nội tiếp được trong đường tròn.c) Đường thẳng BC cắt đường thẳng OM tại I. Chứng minh rằng đường thẳng AI song song với đường thẳng BD.
Đọc tiếp
Cho đường tròn tâm O, đường kính AB và d là một tiếp tuyến của đường tròn (O) tại điểm A. Trên đường thẳng d lấy điểm M (khác A) và trên đoạn OB lấy điểm N (khác O và B). Đường thẳng MN cắt đường tròn (O) tại hai điểm C và D sao cho C nằm giữa M và D. Gọi H là trung điểm của đoạn thẳng CD.
a) Chứng minh tứ giác AOHM nội tiếp được trong đường tròn.
c) Đường thẳng BC cắt đường thẳng OM tại I. Chứng minh rằng đường thẳng AI song song với đường thẳng BD.
Cho đường tròn tâm O, đường kính AB và d là một tiếp tuyến của đường tròn (O) tại điểm A. Trên đường thẳng d lấy điểm M (khác A) và trên đoạn OB lấy điểm N (khác O và B). Đường thẳng MN cắt đường tròn (O) tại hai điểm C và D sao cho C nằm giữa M và D. Gọi H là trung điểm của đoạn thẳng CD.a) Chứng minh tứ giác AOHM nội tiếp được trong đường tròn. c) Đường thẳng BC cắt đường thẳng OM tại I. Chứng minh rằng đường thẳng AI song song với đường thẳng BD.
Đọc tiếp
Cho đường tròn tâm O, đường kính AB và d là một tiếp tuyến của đường tròn (O) tại điểm A. Trên đường thẳng d lấy điểm M (khác A) và trên đoạn OB lấy điểm N (khác O và B). Đường thẳng MN cắt đường tròn (O) tại hai điểm C và D sao cho C nằm giữa M và D. Gọi H là trung điểm của đoạn thẳng CD.
a) Chứng minh tứ giác AOHM nội tiếp được trong đường tròn.
c) Đường thẳng BC cắt đường thẳng OM tại I. Chứng minh rằng đường thẳng AI song song với đường thẳng BD.
cho đường tròn (O) ,từ điểm A nằm ngoài đường tròn kẻ hai tiếp tuyến AB và AC (B,C là hai tiếp điểm).Gọi M là giao điểm OA và BC,D là một điểm nằm trên đường tròn (O) sao cho D không nằm trên đường thẳng OA,kẻ dây cung DE đi qua M.CMR:Tứ giác ADOE nội tiếp.
cho đường tròn (O) ,từ điểm A nằm ngoài đường tròn kẻ hai tiếp tuyến AB và AC (B,C là hai tiếp điểm).Gọi M là giao điểm OA và BC,D là một điểm nằm trên đường tròn (O) sao cho D không nằm trên đường thẳng OA,kẻ dây cung DE đi qua M.CMR:Tứ giác ADOE nội tiếp.
Cho đường tròn(O;R) và đường thẳng (d) không qua O cắt đường tròn tại hai điểm A và B.Từ một điểm M trên (d)(M nằm ngoài đường tròn (O) và A nằm giữa B và M),vẽ hai tiếp tuyến MC,MD của đường tròn (O)(C, D ∈ (O)).Gọi I là trung điểm của AB, tia IO cắt MD tại Ka)Chứng minh 5 điểm:M, C, I, O, D cùng thuộc 1 đường trònb)Chứng minh:KD.KMKO.KIc)Một đường thẳng đi qua O và song song với CD cắt các tia MC,MD lần lượt tại E,F.Xác định vị trí của điểm M trên đường thẳng (d) sao cho diện tích △MEF đ...
Đọc tiếp
Cho đường tròn(O;R) và đường thẳng (d) không qua O cắt đường tròn tại hai điểm A và B.Từ một điểm M trên (d)(M nằm ngoài đường tròn (O) và A nằm giữa B và M),vẽ hai tiếp tuyến MC,MD của đường tròn (O)(C, D ∈ (O)).Gọi I là trung điểm của AB, tia IO cắt MD tại K
a)Chứng minh 5 điểm:M, C, I, O, D cùng thuộc 1 đường tròn
b)Chứng minh:KD.KM=KO.KI
c)Một đường thẳng đi qua O và song song với CD cắt các tia MC,MD lần lượt tại E,F.Xác định vị trí của điểm M trên đường thẳng (d) sao cho diện tích △MEF đạt giá trị nhỏ nhất.
a) Xét đường tròn (O; R) có I là trung điểm của dây AB
=> OI ⊥ AB (liên hệ giữa đường kính và dây cung)
=> ΔMIO vuông tại I => I, M, O cùng thuộc đường tròn đường kính OM
ΔMCO vuông tại C => C, M, O cùng thuộc đương tròn đường kính OM
ΔMDO vuông tại D => D, M, O cùng thuộc đường tròn đường kính OM
=> I, M, O, C, D cùng thuộc đường tròn đường kính OM
b) Xét ΔKOD và ΔKMI có: \(\widehat{KDO}=\widehat{KIM}\) (=90o)
\(\widehat{OKM}\) chung
=> ΔKOD ~ ΔKMI (g.g) => \(\dfrac{KO}{KM}=\dfrac{KD}{KI}\) => KO.KI = KD.KM
c) Xét đường tròn (O; R), tiếp tuyến MC, MD => MO là phân giác \(\widehat{CMD}\); MD = MC
Lại có OC = OD = R => OM là trung trực của CD hay OM ⊥ CD.
Mà CD // EF => OM ⊥ EF. Lại có MO là phân giác \(\widehat{CMD}\)
=> \(\widehat{CMO}=\widehat{DMO}\) => ΔEMO = ΔFMO (g.c.g)
=> SEMO = SFMO =\(\dfrac{1}{2}\)SEMF
Để SEMF nhỏ nhất thì SEMO nhỏ nhất
=> \(\dfrac{1}{2}\)EM.OC = \(\dfrac{1}{2}\).R.EM nhỏ nhất => EM nhỏ nhất (do R cố định)
Ta có: EM = EC + CM ≥ 2\(\sqrt{EC.CM}\)=2R (BĐT Cô-si)
Dấu "=" xảy ra ⇔ EC = CM => OC = CE = CM (t/c đường trung tuyến trong tam giác vuông) => ΔCMO vuông cân tại C => OM = OC\(\sqrt{2}\) =R\(\sqrt{2}\)
Vậy để SEMF nhỏ nhất thì M là giao điểm của (d) và (O; R\(\sqrt{2}\))
Đúng 2
Bình luận (0)
Cho a, b là hai đường thẳng song song và cách nhau một khoảng 3cm. Lấy điểm O trên b và vẽ đường tròn (O; 4 cm). Chứng minh đường tròn này cắt a ở hai điểm phân biệt
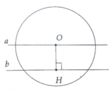
Kẻ OH ⊥ a tại H
Ta có OH=3cm < R nên a cắt (O) tại hai điểm phân biệt
Đúng 0
Bình luận (0)

















