Bài 1:

a. $y=(m-2m+3m-2m+3)x-2=3x-2$

Vì $3\neq 0$ nên hàm này là hàm bậc nhất với mọi $m\in\mathbb{R}$

b. Vì  $3>0$ nên hàm này là hàm đồng biến với mọi $m\in\mathbb{R}$

Bài 2:

Đồ thị xanh lá cây: $y=-x+3$

Đồ thị xanh nước biển: $y=2x+1$

a, \(y=3-4sin^2x.cos^2x=3-sin^22x\)

Đặt \(sin2x=t\left(t\in\left[-1;1\right]\right)\).

\(\Rightarrow y=f\left(t\right)=3-t^2\)

\(\Rightarrow y_{min}=minf\left(t\right)=2\)

\(y_{max}=maxf\left(t\right)=3\)

b, \(y=f\left(t\right)=\dfrac{-2}{3t-5}\left(t\in\left[0;1\right]\right)\)

\(\Rightarrow y_{min}=minf\left(t\right)=\dfrac{2}{5}\)

\(y_{max}=maxf\left(t\right)=1\)

\(y=f\left(x\right)=-x^2+2x+m-4\)

\(f\left(-1\right)=m-7;f\left(2\right)=m-4;f\left(1\right)=m-3\)

\(\Rightarrow miny=f\left(1\right)=m-3=3\Leftrightarrow m=6\)

Lời giải:
a. Để hàm trên là hàm bậc nhất thì $\frac{m-2}{m+3}\neq 0$

\(\Leftrightarrow \left\{\begin{matrix} m-2\neq 0\\ m+3\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\neq 2\\ m\neq -3\end{matrix}\right.\)

b. Để hàm trên đồng biến thì $\frac{m-2}{m+3}>0$

\(\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} m-2>0\\ m+3>0\end{matrix}\right.\\ \left\{\begin{matrix} m-2<0\\ m+3< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} m>2\\ m< -3\end{matrix}\right.\)

Để hàm trên nghịch biến thì $\frac{m-2}{m+3}< 0$

\(\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} m-2>0\\ m+3< 0\end{matrix}\right.\\ \left\{\begin{matrix} m-2< 0\\ m+3>0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} -3> m>2(\text{vô lý}\\ -3< m< 2\end{matrix}\right.\Leftrightarrow -3< m< 2\)

* Hàm số đã cho liên tục trên R vì với 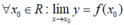 nên (1) đúng

* Tại điểm x = 0 hàm số không có đạo hàm nên (2) sai.

* y = x 2 - 2 | x | + 2 = | x | 2 - 2 | x | + 2 = ( | x | - 1 ) 2 + 1 ≥ 1 ∀ x

Suy ra, GTNN của hàm số là 1 khi |x| = 1 ⇔ x = ±1

nên hàm số không có GTLN.

* Phương trình x 2 - 2 | x | + 2 = 0  vô nghiệm nên đồ thị không cắt trục hoành.

f ( - x ) = ( - x ) 2 - 2 | - x | + 2 = x 2 - 2 | x | + 2 = f ( x )

Nên hàm số đã cho là hàm số chẵn.

Mệnh đề 1, 5 đúng. Mệnh đề 2, 3,4,6 sai.

Chọn B

Hàm nghịch biến trên R khi:

\(3-2k< 0\Rightarrow k>\dfrac{3}{2}\)

để hàm số nghịch biên thì\(3-2k< 0\Rightarrow2k>3\Rightarrow k>\dfrac{3}{2}\)

Để hàm số \(y=\left(3-2k\right)x+2\) nghịch biến trên R thì \(3-2k< 0\Leftrightarrow3< 2k\Leftrightarrow k>\dfrac{3}{2}\)

a, với m = 1 thay m = 1 vào hàm số : y = ( 3-2m)x+ m-1 ta có :

y = ( 3-2.1)x+1-1

y = x 

Đồ thị hàm số giao với trục Ox tại điểm có tung độ bằng 0 nên; y =0

=> x = 0

Đồ thị hàm số đi qua điểm O(0;0)

với x = 1 => y = 1 .

Đồ thị đi qua A(1;1)

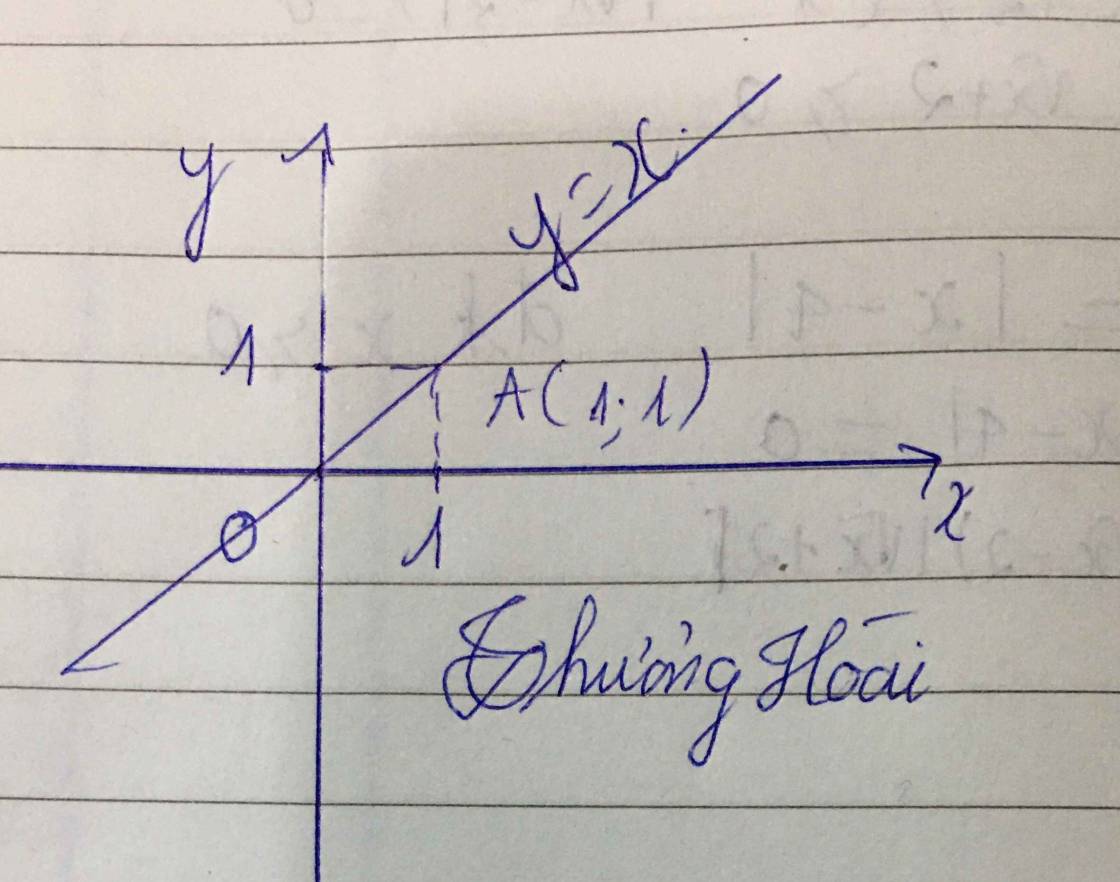
b, Gọi B (x₁;y1) là giao điểm của  hàm số y= (3-2m)x + m-1và hàm số  

2x-3 = 0 .

Theo bài ra ta có: y1 = 0 => (3-2m)x₁ + m - 1 = 0

Vì B là giao điểm của hai đt nên tọa độ điểm B  thỏa mãn hàm số :

2x - 3 = 0=> 2x₁ - 3 = 0 => x₁ = 3/2

Thay x₁ = 3/2 vào pt (3-2m)x₁ +m -1 = 0 ta có :

                                 (3-2m) .3/2  + m - 1 = 0 

                                 9/2 - 3m + m - 1 = 0

                                  -2m + 7/2 = 0

                                     m = 7/4

Kết luận với m = 7/4 thì đồ thị hàm số : y =( 3-2m)x+m-1

có dạng : y = -1/2x + 3/4 và giao với đồ thị 2x-3 = 0 tại điểm B( 3/2; 0)

và điểm B nằm trục hoành