Cho hai vectơ \(\overrightarrow{u}=\left(1;-2;3\right)\) và \(\overrightarrow{v}=\left(3;4;-5\right)\). Hãy chỉ ra tọa độ của một vectơ \(\overrightarrow{w}\) khác \(\overrightarrow{0}\) vuông góc với cả hai vectơ \(\overrightarrow{u}\) và \(\overrightarrow{v}\).

Những câu hỏi liên quan
Trong mặt phẳng toạ độ Oxy (Hình 18), cho hai vectơ overrightarrow u left( {{x_1},{y_1}} right) và overrightarrow v left( {{x_2},{y_2}} right)a) Biểu diễn các vectơ overrightarrow u ,overrightarrow v theo hai vectơ overrightarrow i và overrightarrow j b) Biểu diễn các vectơ overrightarrow u + overrightarrow v ,overrightarrow u - overrightarrow v ,koverrightarrow u left( {k in mathbb{R}} right) theo hai vectơ overrightarrow i và overrightarrow j c) Tìm tọa độ của các vectơ overrightarrow...
Đọc tiếp
Trong mặt phẳng toạ độ Oxy (Hình 18), cho hai vectơ \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\) và \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\)
a) Biểu diễn các vectơ \(\overrightarrow u ,\overrightarrow v \) theo hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \)
b) Biểu diễn các vectơ \(\overrightarrow u + \overrightarrow v \),\(\overrightarrow u - \overrightarrow v \),\(k\overrightarrow u \left( {k \in \mathbb{R}} \right)\) theo hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \)
c) Tìm tọa độ của các vectơ \(\overrightarrow u + \overrightarrow v \),\(\overrightarrow u - \overrightarrow v \),\(k\overrightarrow u \left( {k \in \mathbb{R}} \right)\)
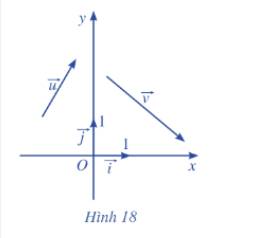
a) Do \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\) nên \(\overrightarrow u = {x_1}\overrightarrow i + {y_1}\overrightarrow j .\), \(\overrightarrow v = {x_2}\overrightarrow i + {y_2}\overrightarrow j .\)
b) +) \(\overrightarrow u + \overrightarrow v = \left( {{x_1}\overrightarrow i + {y_1}\overrightarrow j } \right) + \left( {{x_2}\overrightarrow i + {y_2}\overrightarrow j } \right) = \left( {{x_1}\overrightarrow i + {x_2}\overrightarrow i } \right) + \left( {{y_1}\overrightarrow j + {y_2}\overrightarrow j } \right) = \left( {{x_1} + {x_2}} \right)\overrightarrow i + \left( {{y_1} + {y_2}} \right)\overrightarrow j \)
+) \(\overrightarrow u - \overrightarrow v = \left( {{x_1}\overrightarrow i + {y_1}\overrightarrow j } \right) - \left( {{x_2}\overrightarrow i + {y_2}\overrightarrow j } \right) = \left( {{x_1}\overrightarrow i - {x_2}\overrightarrow i } \right) + \left( {{y_1}\overrightarrow j - {y_2}\overrightarrow j } \right) = \left( {{x_1} - {x_2}} \right)\overrightarrow i + \left( {{y_1} - {y_2}} \right)\overrightarrow j \)
+) \(k\overrightarrow u = \left( {k{x_1}} \right)\overrightarrow i + \left( {k{y_1}} \right)\overrightarrow j \)
c) Tọa độ của các vectơ \(\overrightarrow u + \overrightarrow v \),\(\overrightarrow u - \overrightarrow v \),\(k\overrightarrow u \left( {k \in \mathbb{R}} \right)\)lần lượt là:
\(\left( {{x_1} + {x_2};{y_1} + {y_2}} \right),\left( {{x_1} - {x_2};{y_1} - {y_2}} \right),\left( {k{x_1},k{y_1}} \right)\)
Đúng 0
Bình luận (0)
Cho hai overrightarrow{u}và overrightarrow{v}có giá vuông góc với nhau. dựng vectơ overrightarrow{w}left(frac{left|overrightarrow{u}right|+left|overrightarrow{v}right|}{left|overrightarrow{u}+overrightarrow{v}right|}-1right)left(overrightarrow{u}+overrightarrow{v}right)-left(frac{left|overrightarrow{u}right|}{left|overrightarrow{u}right|+left|overrightarrow{u}+overrightarrow{v}right|}overrightarrow{v}+frac{left|overrightarrow{v}right|}{left|overrightarrow{v}right|+left|overrightarrow{u}+overrigh...
Đọc tiếp
Cho hai \(\overrightarrow{u}\)và \(\overrightarrow{v}\)có giá vuông góc với nhau. dựng vectơ
\(\overrightarrow{w}=\left(\frac{\left|\overrightarrow{u}\right|+\left|\overrightarrow{v}\right|}{\left|\overrightarrow{u}+\overrightarrow{v}\right|}-1\right)\left(\overrightarrow{u}+\overrightarrow{v}\right)-\left(\frac{\left|\overrightarrow{u}\right|}{\left|\overrightarrow{u}\right|+\left|\overrightarrow{u}+\overrightarrow{v}\right|}\overrightarrow{v}+\frac{\left|\overrightarrow{v}\right|}{\left|\overrightarrow{v}\right|+\left|\overrightarrow{u}+\overrightarrow{v}\right|}\overrightarrow{u}\right)\)
chứng minh vectơ \(\overrightarrow{w}\)có giá vuông góc với giá của vectơ \(\overrightarrow{u}+\overrightarrow{v}\)
MÌNH ĐANG CẦN NGAY TRONG TỐI NAY MONG CÁC BẠN CÓ THỂ GIÚP MÌNH
CẢM ƠN CÁC BẠN RẤT NHIỀU
Trong mặt phẳng Oxy, cho hai đường thẳng Delta đi qua điểm {M_0}left( {{x_0};{y_0}} right) và vectơ overrightarrow n left( {a;b} right) và overrightarrow u left( {b; - a} right) khác vectơ 0. Cho biết overrightarrow u có giá song song hoặc trùng với Delta .a) Tính tích vô hướng overrightarrow n overrightarrow {.u} và nêu nhận xét về phương của hai vectơ overrightarrow n ,overrightarrow u b) Gọi Mleft( {x;y} right) là điểm di động trên Delta . Chứng tỏ rằng vectơ overrightarrow {{M_0}M} l...
Đọc tiếp
Trong mặt phẳng Oxy, cho hai đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và vectơ \(\overrightarrow n = \left( {a;b} \right)\) và \(\overrightarrow u = \left( {b; - a} \right)\) khác vectơ 0. Cho biết \(\overrightarrow u \) có giá song song hoặc trùng với \(\Delta \).
a) Tính tích vô hướng \(\overrightarrow n \overrightarrow {.u} \) và nêu nhận xét về phương của hai vectơ \(\overrightarrow n ,\overrightarrow u \)
b) Gọi \(M\left( {x;y} \right)\) là điểm di động trên \(\Delta \). Chứng tỏ rằng vectơ \(\overrightarrow {{M_0}M} \) luôn cùng phương với vectơ \(\overrightarrow u \) và luôn vuông góc với vectơ \(\overrightarrow n \)
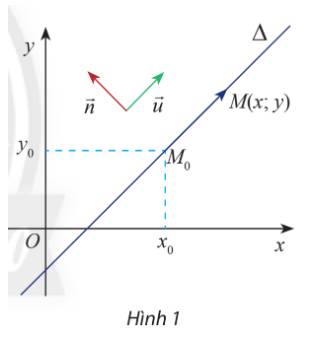
a) Ta có \(\overrightarrow n .\overrightarrow u = a.b + b.( - a) = 0\)
Tích vô hướng bằng 0 nên hai vectơ \(\overrightarrow n ,\overrightarrow u \)có phương vuông góc với nhau
b) Vectơ \(\overrightarrow {{M_0}M} \) có giá là đường thẳng \(\Delta\)
=> luôn cùng phương với vectơ \(\overrightarrow u \)
=> vectơ \(\overrightarrow {{M_0}M} \) có phương vuông góc với vectơ \(\overrightarrow n \)
Đúng 0
Bình luận (0)
Cho hai vectơ cho hai vectơ overrightarrow a ,overrightarrow b và điểm M như hình 3.a) Hãy vẽ vectơ overrightarrow {MN} 3overrightarrow a ,overrightarrow {MP} - 3overrightarrow b b) Cho biết mỗi ô có cạnh bằng 1. Tính: left| {3overrightarrow b } right|,left| { - 3overrightarrow b } right|,left| {2overrightarrow a + 2overrightarrow b } right|.
Đọc tiếp
Cho hai vectơ cho hai vectơ \(\overrightarrow a ,\overrightarrow b \) và điểm M như hình 3.
a) Hãy vẽ vectơ \(\overrightarrow {MN} = 3\overrightarrow a ,\overrightarrow {MP} = - 3\overrightarrow b \)
b) Cho biết mỗi ô có cạnh bằng 1. Tính: \(\left| {3\overrightarrow b } \right|,\left| { - 3\overrightarrow b } \right|,\left| {2\overrightarrow a + 2\overrightarrow b } \right|\).

a) \(\overrightarrow {MN} = 3\overrightarrow a \)có độ dài bằng 3 lần vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \)
Suy ra, từ điểm M vẽ vectơ MN với độ dài là 6 ô vuông và có hướng từ trái sang phải
\(\overrightarrow {MP} = - 3\overrightarrow b \)có độ dài bằng 3 lần vectơ \( - \overrightarrow b \), ngược hướng với vectơ \(\overrightarrow b \)
Suy ra, từ điểm M vẽ vectơ MP với độ dài là 3 đường chéo ô vuông và có hướng từ trên xuống dưới chếch sang trái
b) Hình vuông với cạnh bằng 1 thì ta tính được đường chéo có độ dài là \(\sqrt 2 \); \(\left| {\overrightarrow b } \right| = \sqrt 2 \) . Suy ra:
\(\left| {3\overrightarrow b } \right| = 3\left| {\overrightarrow b } \right| = 3\sqrt 2 \); \(\left| { - 3\overrightarrow b } \right| = 3\left| {\overrightarrow { - b} } \right| = 3\sqrt 2 \); \(\left| {2\overrightarrow a + 2\overrightarrow b } \right| = \left| {2\left( {\overrightarrow a + \overrightarrow b } \right)} \right| = 2\left| {\overrightarrow a + \overrightarrow b } \right|\)
Từ điểm cuối của vectơ \(\overrightarrow a \) vẽ một vectơ bằng vectơ \(\overrightarrow b \) ta có \(\overrightarrow c = \overrightarrow a + \overrightarrow b \)
Áp dụng định lý cosin ta tính được độ dài của vectơ \(\overrightarrow c \)là \(\left| {\overrightarrow c } \right| = \sqrt {{{\left| {\overrightarrow a } \right|}^2} + {{\left| {\overrightarrow b } \right|}^2} - 2\left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|\cos \left( {\widehat {\overrightarrow a ,\overrightarrow b }} \right)} = \sqrt {{2^2} + {{\sqrt 2 }^2} - 2.2.\sqrt 2 .\cos \left( {135^\circ } \right)} = \sqrt {10} \)
\( \Rightarrow \left| {2\overrightarrow a + 2\overrightarrow b } \right| = 2\left| {\overrightarrow a + \overrightarrow b } \right| = 2\left| {\overrightarrow c } \right| = 2\sqrt {10} \)

Đúng 0
Bình luận (0)
Cho vectơ \(\overrightarrow a \). Hãy xác định độ dài và hướng của hai vectơ \(\overrightarrow a + \overrightarrow a ,\left( { - \overrightarrow a } \right) + \left( { - \overrightarrow a } \right)\): (Hình 1)
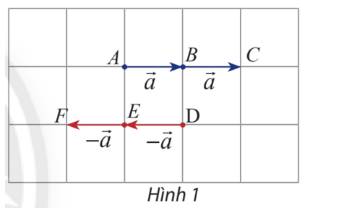
Dựa vào hình 1 ta thấy
Vectơ \(\overrightarrow a + \overrightarrow a = \overrightarrow {AC} \) có độ dài bằng 2 lần vectơ \(\overrightarrow a \)và cùng hướng với vectơ \(\overrightarrow a \)
Vectơ \(\left( { - \overrightarrow a } \right) + \left( { - \overrightarrow a } \right)= \overrightarrow {DF}\) có độ dài bằng 2 lần vectơ \(\left( { - \overrightarrow a } \right)\) và cùng hướng với vectơ \(\left( { - \overrightarrow a } \right)\)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho hai vectơ overrightarrow{u}left(3;-4right);overrightarrow{v}left(2;5right)
a) Tìm tọa độ của vectơ overrightarrow{a}2overrightarrow{u}+3overrightarrow{v}
b) Tìm tọa độ của vectơ overrightarrow{b}overrightarrow{u}-overrightarrow{v}
c) Tìm m sao cho overrightarrow{c}left(m;10right) và overrightarrow{v} cùng phương
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hai vectơ \(\overrightarrow{u}=\left(3;-4\right);\overrightarrow{v}=\left(2;5\right)\)
a) Tìm tọa độ của vectơ \(\overrightarrow{a}=2\overrightarrow{u}+3\overrightarrow{v}\)
b) Tìm tọa độ của vectơ \(\overrightarrow{b}=\overrightarrow{u}-\overrightarrow{v}\)
c) Tìm m sao cho \(\overrightarrow{c}=\left(m;10\right)\) và \(\overrightarrow{v}\) cùng phương
a) \(\overrightarrow{a}=2\overrightarrow{u}+3\overrightarrow{v}=2\left(3;-4\right)+3\left(2;5\right)=\left(6;-8\right)+\left(6;15\right)\)\(=\left(12;7\right)\).
b) \(\overrightarrow{b}=\overrightarrow{u}-\overrightarrow{v}=\left(3;-4\right)-\left(2;5\right)=\left(1;-9\right)\).
c) Hai véc tơ \(\overrightarrow{c}=\left(m;10\right)\) và \(\overrightarrow{v}\) cùng phương khi và chỉ khi:
\(\dfrac{m}{2}=\dfrac{10}{5}=2\Rightarrow m=4\).
Đúng 0
Bình luận (0)
Tích vô hướng và góc giữa hai vectơ \(\overrightarrow u = \left( {0; - 5} \right),\;\overrightarrow v = \left( {\sqrt 3 ;1} \right)\)
Ta có: \(\overrightarrow u = \left( {0; - 5} \right),\;\overrightarrow v = \left( {\sqrt 3 ;1} \right)\)
\( \Rightarrow \overrightarrow u .\;\,\overrightarrow v = 0.\sqrt 3 + \left( { - 5} \right).1 = - 5.\)
Đúng 0
Bình luận (0)
Cho hai vectơ cùng phương \(\overrightarrow u = \left( {x;y} \right)\) và \(\overrightarrow v = \left( {kx;ky} \right)\). Hãy kiểm tra công thức \(\overrightarrow u .\overrightarrow v = k\left( {{x^2} + {y^2}} \right)\) theo từng trường hợp sau:
a) \(\overrightarrow u = \overrightarrow 0 \)
b) \(\overrightarrow u \ne \overrightarrow 0 \) và \(k \ge 0\)
c) \(\overrightarrow u \ne \overrightarrow 0 \) và \(k < 0\)
a) Vì \(\overrightarrow u = \overrightarrow 0 \) nên \(\overrightarrow u \) vuông góc với mọi \(\overrightarrow v \).
Như vậy \(\overrightarrow u .\overrightarrow v = 0\)
Mặt khác: \(\overrightarrow u = \overrightarrow 0 \Leftrightarrow x = y = 0\)
\( \Rightarrow k\left( {{x^2} + {y^2}} \right) = 0 = \overrightarrow u .\overrightarrow v \)
b) Vì \(\overrightarrow u \ne \overrightarrow 0 \) và \(k \ge 0\) nên \(\overrightarrow u \) và \(\overrightarrow v \)cùng hướng.
\( \Rightarrow \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = {0^o} \Leftrightarrow \cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = 1\)
\(\begin{array}{l} \Rightarrow \overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right| = \sqrt {{x^2} + {y^2}} .\sqrt {{{\left( {kx} \right)}^2} + {{\left( {ky} \right)}^2}} \\ = \sqrt {{x^2} + {y^2}} .\left| k \right|.\sqrt {{x^2} + {y^2}} = k\left( {{x^2} + {y^2}} \right)\end{array}\)
(|k|= k do k > 0)
c) Vì \(\overrightarrow u \ne \overrightarrow 0 \) và \(k < 0\) nên \(\overrightarrow u \) và \(\overrightarrow v \)ngược hướng.
\( \Rightarrow \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = {180^o} \Leftrightarrow \cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = - 1\)
\(\begin{array}{l} \Rightarrow \overrightarrow u .\;\overrightarrow v = - \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right| = - \sqrt {{x^2} + {y^2}} .\sqrt {{{\left( {kx} \right)}^2} + {{\left( {ky} \right)}^2}} \\ = - \sqrt {{x^2} + {y^2}} .\left| k \right|.\sqrt {{x^2} + {y^2}} = k\left( {{x^2} + {y^2}} \right).\end{array}\)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho hai vectơ không cùng phương overrightarrow u left( {x;y} right) và overrightarrow v left( {xy} right).a) Xác định tọa độ của các điểm A và B sao cho overrightarrow {OA} overrightarrow u ,;overrightarrow {OB} overrightarrow v .b) Tính A{B^2},O{A^2},O{B^2} theo tọa độ của A và B.c) Tính overrightarrow {OA} .overrightarrow {OB} theo tọa độ của A, B.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hai vectơ không cùng phương \(\overrightarrow u = \left( {x;y} \right)\) và \(\overrightarrow v = \left( {x'y'} \right)\).
a) Xác định tọa độ của các điểm A và B sao cho \(\overrightarrow {OA} = \overrightarrow u ,\;\overrightarrow {OB} = \overrightarrow v .\)
b) Tính \(A{B^2},O{A^2},O{B^2}\) theo tọa độ của A và B.
c) Tính \(\overrightarrow {OA} .\overrightarrow {OB} \) theo tọa độ của A, B.
a) Vì \(\overrightarrow {OA} = \overrightarrow u = (x;y)\) nên A(x; y).
Tương tự: do \(\overrightarrow {OB} = \overrightarrow v = \left( {x'y'} \right)\) nên B (x’; y’)
b) Ta có: \(\overrightarrow {OA} = (x;y) \Rightarrow O{A^2} = {\left| {\overrightarrow {OA} } \right|^2} = {x^2} + {y^2}.\)
Và \(\overrightarrow {OB} = (x'y') \Rightarrow O{B^2} = {\left| {\overrightarrow {OB} } \right|^2} = x{'^2} + y{'^2}.\)
Lại có: \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = \left( {x'y'} \right) - \left( {x;y} \right) = \left( {x' - x;y' - y} \right)\)
\( \Rightarrow A{B^2} = {\left| {\overrightarrow {AB} } \right|^2} = {\left( {x' - x} \right)^2} + {\left( {y' - y} \right)^2}.\)
c) Theo định lí cosin trong tam giác OAB ta có:
\(\cos \widehat O = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}}\)
Mà \(\overrightarrow {OA} .\overrightarrow {OB} = \left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|.\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = OA.OB.\cos \widehat O\)
\( \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = OA.OB.\frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}} = \frac{{O{A^2} + O{B^2} - A{B^2}}}{2}\)
\(\begin{array}{l} \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = \frac{{{x^2} + {y^2} + x{'^2} + y{'^2} - {{\left( {x' - x} \right)}^2} - {{\left( {y' - y} \right)}^2}}}{2}\\ \Leftrightarrow \overrightarrow {OA} .\overrightarrow {OB} = \frac{{ - \left( { - 2x'.x} \right) - \left( { - 2y'.y} \right)}}{2} = x'.x + y'.y\end{array}\)
Đúng 0
Bình luận (0)
a) Cho \(\overrightarrow u = \left( { - 2;0} \right),\overrightarrow v = \left( {0;6} \right),\overrightarrow w = \left( { - 2;3} \right)\). Tìm tọa độ vectơ \(\overrightarrow u + \overrightarrow v + \overrightarrow w \)
b) Cho \(\overrightarrow u = \left( {\sqrt 3 ;0} \right),\overrightarrow v = \left( {0;\sqrt 7 } \right)\). Tìm tọa độ của vectơ \(\overrightarrow w \)sao cho \(\overrightarrow w + \overrightarrow u = \overrightarrow v \)
a) Tọa độ của vectơ \(\overrightarrow u + \overrightarrow v + \overrightarrow w \) là: \(\overrightarrow u + \overrightarrow v + \overrightarrow w = \left( { - 2 + 0 + \left( { - 2} \right);0 + 6 + 3} \right) = \left( { - 4;9} \right)\)
b) Ta có: \(\overrightarrow w + \overrightarrow u = \overrightarrow v \Leftrightarrow \overrightarrow w = \overrightarrow v - \overrightarrow u \) nên \(\overrightarrow w = \left( {0 - \sqrt 3 ; - \sqrt 7 - 0} \right) = \left( { - \sqrt 3 ; - \sqrt 7 } \right)\)
Đúng 0
Bình luận (0)








