cho AB là dây của (O;12cm).Biết AB =12cm.Tính diện tích hình quạt tạo bởi hai bán kính OA,OB và cung nhỏ AB

Những câu hỏi liên quan
cho AB là dây của đường tròn (O;R). Biết AB=R khoảng cách từ tâm O đến dây AB là
Gọi H là trung điểm AB \(\Rightarrow OH\perp AB\Rightarrow OH\) là k/c từ O đến AB
Ta có: \(AH=\dfrac{1}{2}AB=\dfrac{R}{2}\)
Áp dụng định lý Pitago cho tam giác vuông OAH:
\(OA^2=OH^2+AH^2\Leftrightarrow R^2=OH^2+\left(\dfrac{R}{2}\right)^2\)
\(\Rightarrow OH=\dfrac{R\sqrt{3}}{2}\)
Đúng 0
Bình luận (0)
Cho (O;13cm), M là trung điểm của dây AB sao cho OM = 5cm. Độ dài dây AB là
Cho (O;R), dây AB (AB <2R). Gọi P là điểm chính giữa dây cung nhỏ AB. Gọi C là điểm bất kì nằm trên dây AB. PC cắt (O) tại D. c/m PA là tiếp tuyến của (ACD)
P là điểm chính giữa của cung nhỏ AB
=>\(sđ\stackrel\frown{PA}=sđ\stackrel\frown{PB}\)
Xét (O) có
\(\widehat{ADP}\) là góc nội tiếp chắn cung AP
\(\widehat{BAP}\) là góc nội tiếp chắn cung PB
\(sđ\stackrel\frown{PA}=sđ\stackrel\frown{PB}\)
Do đó: \(\widehat{ADP}=\widehat{BAP}\)
Trên nửa mặt phẳng bờ AB có chứa điểm P, kẻ tia Ax là tiếp tuyến của đường tròn ngoại tiếp ΔACD
Khi đó, ta sẽ có:
\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC của đường tròn ngoại tiếp ΔACD
\(\widehat{ADC}\) là góc nội tiếp chắn cung AC của đường tròn ngoại tiếp ΔACD
Do đó: \(\widehat{xAC}=\widehat{ADC}\)
mà \(\widehat{ADP}=\widehat{ADC}=\widehat{BAP}\)
nên \(\widehat{xAC}=\widehat{BAP}\)
=>\(\widehat{xAC}=\widehat{CAP}\)
=>Ax và AP là hai tia trùng nhau
=>PA là tiếp tuyến của (ACD)
Đúng 1
Bình luận (0)
Cho đường tròn tâm o bán kính 7dm. AB là dây của đường tròn.Tính độ dài của dây AB biết
Biết khoảng cách từ tâm o đến dây AB là 4dm.
Kẻ d(O;AB) = OH
khi đó OH = 4 dm
Xét tam giác AHO vuông tại H, theo định lí Pytago ta có :
\(AO^2=AH^2+HO^2\Rightarrow AH^2=AO^2-HO^2=49-16=33\Rightarrow AH=\sqrt{33}\)dm
mà OH vuông AB => H là trung điểm AB
hay \(AB=2AH=2\sqrt{33}\)dm
Cho đường tròn (O) và dây AB khác đường kinh. Qua O kẻ tia Ox vuông góc với dây AB tại I, cắt tiếp tuyến tại A của đường tròn (O) ở điểm M. a) Cho bản kinh của đường tròn (O) bằng 10cm, OI = 6cm Tính độ dài dây AB. b) Chứng minh MB là tiếp tuyến của đường tròn (O). c) Kẻ đường kính AD của (O), chứng minh BDI = overline OMD
a: \(AI=\sqrt{10^2-6^2}=8\left(cm\right)\)
AB=2*AI=16cm
b: ΔOAB cân tại O
mà OI là đường cao
nên OI là phân giác của góc AOB
Xét ΔOAM và ΔOBM có
OA=OB
góc AOM=góc BOM
OM chung
Do đó: ΔOAM=ΔOBM
=>góc OBM=90 độ
=>MB là tiêp tuyến của (O)
Đúng 0
Bình luận (0)
Cho đường tròn (O;5cm) và dây cung AB =6 cm. Gọi E là trung điểm của AB, OE cắt (O) tại M. Độ dài dây AM là:
Cho (O) có dây AB khác đường kính . Qua O kẻ đường vuông góc với AB tại H và cắt tiếp tuyến tại A của đường tròn ở điểm M.a) Chứng minh : H là trung điểm của đoạn AB và MB là tiếp tuyến của (O) tại Bb) Vẽ dây AC của (O) sao cho AC//OM . Chứng minh : 3 điểm B,O,D thẳng hàng c) Gọi D và I lần lượt là giao điểm của MC với (O) và AB. Chứng minh : góc OHC góc MHD và ID . HC IC . HD
Đọc tiếp
Cho (O) có dây AB khác đường kính . Qua O kẻ đường vuông góc với AB tại H và cắt tiếp tuyến tại A của đường tròn ở điểm M.
a) Chứng minh : H là trung điểm của đoạn AB và MB là tiếp tuyến của (O) tại B
b) Vẽ dây AC của (O) sao cho AC//OM . Chứng minh : 3 điểm B,O,D thẳng hàng
c) Gọi D và I lần lượt là giao điểm của MC với (O) và AB. Chứng minh : góc OHC = góc MHD và ID . HC = IC . HD
a: Ta có: ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB và OH là phân giác của \(\widehat{AOB}\)
ta có: OH là phân giác của góc AOB
=>OM là phân giác của góc AOB
=>\(\widehat{AOM}=\widehat{BOM}\)
Xét ΔOAM và ΔOBM có
OA=OB
\(\widehat{AOM}=\widehat{BOM}\)
OM chung
Do đó: ΔOAM=ΔOBM
=>\(\widehat{OBM}=\widehat{OAM}\)
mà \(\widehat{OAM}=90^0\)
nên \(\widehat{OBM}=90^0\)
=>MB là tiếp tuyến của (O)
b: Sửa đề: B,O,C thẳng hàng
Ta có: AB\(\perp\)OM
OM//AC
Do đó: AB\(\perp\)AC
=>ΔABC vuông tại A
Vì ΔABC vuông tại A
nên ΔABC nội tiếp đường tròn đường kính BC
mà ΔABC nội tiếp (O)
nên O là trung điểm của BC
=>B,O,C thẳng hàng
c: Xét (O) có
ΔDBC nội tiếp
BC là đường kính
Do đó: ΔDBC vuông tại D
=>BD\(\perp\)DC tại D
=>BD\(\perp\)CM tại D
Xét ΔBCM vuông tại B có BD là đường cao
nên \(MD\cdot MC=MB^2\)(1)
Xét ΔBOM vuông tại B có BH là đường cao
nên \(MH\cdot MO=MB^2\left(2\right)\)
Từ (1) và (2) suy ra \(MD\cdot MC=MH\cdot MO\)
=>\(\dfrac{MD}{MO}=\dfrac{MH}{MC}\)
Xét ΔMDH và ΔMOC có
\(\dfrac{MD}{MO}=\dfrac{MH}{MC}\)
\(\widehat{DMH}\) chung
Do đó: ΔMDH đồng dạng với ΔMOC
=>\(\widehat{MHD}=\widehat{MCO}\)
=>\(\widehat{MHD}=\widehat{OCD}\)
mà \(\widehat{OCD}=\widehat{ODC}\)(ΔOCD cân tại O)
nên \(\widehat{MHD}=\widehat{ODC}\left(3\right)\)
Ta có: \(\widehat{MHD}=\widehat{MCO}\)
mà \(\widehat{MHD}+\widehat{OHD}=180^0\)(hai góc kề bù)
nên \(\widehat{MCO}+\widehat{OHD}=180^0\)
=>\(\widehat{OCD}+\widehat{OHD}=180^0\)
=>OHDC là tứ giác nội tiếp
=>\(\widehat{OHC}=\widehat{ODC}\left(4\right)\)
Từ (3) và (4) suy ra \(\widehat{OHC}=\widehat{MHD}\)
Đúng 0
Bình luận (0)
Cho AB là dây của đường tròn ( O; R). Tính độ dài dây AB trong các trường hợp sau:
a) AOB= 120 độ
b) Khoảng cách từ tâm O đến AB là \(\dfrac{R}{2}\)
a) Kẻ \(OH\perp AB\) tại H
Suy ra H là trung điểm của AB
Xét tam giác cân OAB ( do OA=OB=R) có OH vừa là đg trung tuyến, vừa là đường cao, vừa là đường phân giác
Áp dụng hệ thức lượng vào tam giác vuông OAH có:
\(\sin\widehat{AOH}=\dfrac{AH}{AO}\Leftrightarrow AH=sin60^0.AO=\dfrac{\sqrt{3}R}{2}\)
\(\Leftrightarrow\dfrac{AB}{2}=\dfrac{\sqrt{3}R}{2}\Leftrightarrow AB=R\sqrt{3}\)
Vậy...
b) Áp dụng hệ thức lượng vào tam giác vuông OAH có:
\(tan\widehat{AOH}=\dfrac{AH}{OH}\Leftrightarrow AH=tan60^0.\dfrac{R}{2}=\dfrac{R\sqrt{3}}{2}\)
\(\Leftrightarrow\dfrac{AB}{2}=\dfrac{R\sqrt{3}}{2}\Leftrightarrow AB=R\sqrt{3}\)
Vậy...
Đúng 3
Bình luận (0)
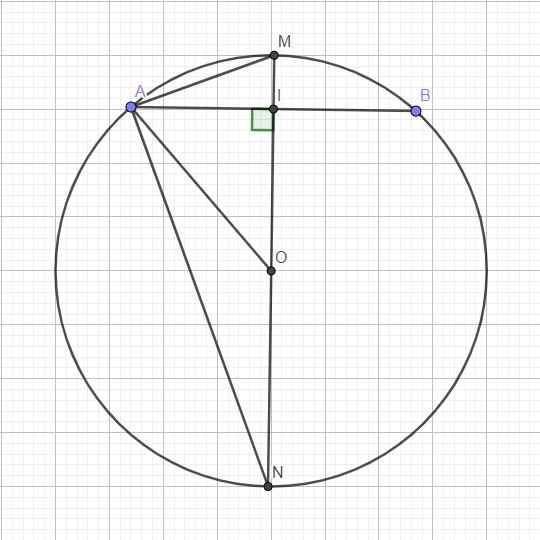
Cho đường tròn (O;R) và một dây cung AB. Gọi I là trung điểm của AB, tia OR cắt cung AB tại M.
a) Cho R=5cm, AB=6cm. Tính AM.
b) Cho MN là đường kính của (O;R), biết AN=10cm và dây AB=12cm. Tính bán kính R.
Cứu giùm với ạTvT
Do I là trung điểm AB \(\Rightarrow OI\perp AB\)
\(AI=\dfrac{1}{2}AB=3\)
Trong tam giác vuông OAI, áp dụng Pitago:
\(OI=\sqrt{OA^2-AI^2}=\sqrt{R^2-AI^2}=4\)
\(\Rightarrow IM=OM-OI=R-OI=1\)
\(\Rightarrow AM=\sqrt{AI^2+IM^2}=\sqrt{10}\left(cm\right)\)
b.
Vẫn như trên, ta có: \(AI=\dfrac{1}{2}AB=6\)
Do MN là đường kính \(\Rightarrow\Delta MAN\) vuông tại A
Áp dụng hệ thức lượng trong tam giác vuông MAN với đường cao AI:
\(\dfrac{1}{AI^2}=\dfrac{1}{AN^2}+\dfrac{1}{AM^2}\Rightarrow\dfrac{1}{6^2}=\dfrac{1}{10^2}+\dfrac{1}{AM^2}\Rightarrow AM=\dfrac{15}{2}\)
Áp dụng hệ thức lượng:
\(AI.MN=AN.AM\Leftrightarrow MN=\dfrac{AM.AN}{AI}=\dfrac{25}{2}\)
\(\Rightarrow R=\dfrac{MN}{2}=\dfrac{25}{4}\left(cm\right)\)
Đúng 2
Bình luận (0)
1 . Cho đường tròn (O;13 cm) , dây AB24cma) Tính khoảng cách từ tâm O đến dây AB?b) Gọi M là điểm thuộc dây AB. Qua M, vẽ dây CD vuông góc với dây AB tại điểm M. Xác định vị trí điểm M trên dây AB để ABCD2 . Cho đường tròn (O) và 2 điểm A,B phân biệt thuộc (O) sao cho đường thẳng AB không đi qua tâm O trên tia đối của tia AB lấy điểm M khác điểm A, từ điểm M kẻ 2 tiếp tuyến phân biệt M E ,MF với đường tròn .GỌI H là trung điểm của dây cung AB , các điểm K và I theo thứ tự là giao điểm của đường...
Đọc tiếp
1 .
Cho đường tròn (O;13 cm) , dây AB=24cm
a) Tính khoảng cách từ tâm O đến dây AB?
b) Gọi M là điểm thuộc dây AB. Qua M, vẽ dây CD vuông góc với dây AB tại điểm M. Xác định vị trí điểm M trên dây AB để AB=CD
2 .
Cho đường tròn (O) và 2 điểm A,B phân biệt thuộc (O) sao cho đường thẳng AB không đi qua tâm O trên tia đối của tia AB lấy điểm M khác điểm A, từ điểm M kẻ 2 tiếp tuyến phân biệt M E ,MF với đường tròn .GỌI H là trung điểm của dây cung AB , các điểm K và I theo thứ tự là giao điểm của đường thẳng EF với các đường thẳng OM
1 cm m,o,h,e,f cùng nằm trên 1 đường tròn
2 oh .oi=ok.om
3Cm IA,IB là các tiếp tuyến của đường tròn