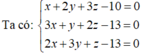Ta có: \(\left(\sqrt{x+y}\right)^2=\left(\sqrt{x-z}+\sqrt{y-z}\right)^2\)

\(\Leftrightarrow\)\(x+y=x+y-2z+2\sqrt{\left(x-z\right)\left(y-z\right)}\)

\(\Leftrightarrow2z=2\sqrt{\left(x-z\right)\left(y-z\right)}\)

Theo giả thiết, ta có: 

theo giả thiết, ta có: \(\frac{1}{x}+\frac{1}{y}-\frac{1}{z}=0\Rightarrow\frac{1}{z}-\frac{1}{x}=\frac{1}{y}\)\(\Rightarrow\frac{x-z}{zx}=\frac{1}{y}\Rightarrow x-z=\frac{zx}{y}\)

Tương tự, ta có: \(y-z=\frac{zy}{x}\)

Do đó: \(2\sqrt{\left(x-z\right)\left(y-z\right)}=2\sqrt{\frac{zx}{y}.\frac{zy}{x}}=2z\) (1)

ta có: \(\left(\sqrt{x+y}\right)^2=\left(\sqrt{x-z}+\sqrt{y-z}\right)^2\)

\(\Leftrightarrow2z=2\sqrt{\left(x-z\right)\left(y-z\right)}\)(2)

Thay (2) vào (1) ta thấy (2) luôn đúng

Suy ra ĐPCM

Vì \(x>0,y>0\Rightarrow\frac{1}{x}>0;\frac{1}{y}>0\)

mà \(\frac{1}{x}+\frac{1}{y}-\frac{1}{z}=0\Rightarrow\frac{1}{z}=\frac{1}{x}+\frac{1}{y}\Rightarrow\frac{1}{z}>0\Rightarrow z>0\)

Ta có: \(\frac{1}{x}+\frac{1}{y}-\frac{1}{z}=0\Leftrightarrow yz+zx-xy=0\)

\(\Leftrightarrow-z^2=-z^2+yz+zx-xy=-\left(x-z\right)\left(y-z\right)\)

\(\Leftrightarrow z^2=\left(x-z\right)\left(y-z\right)>0\)

\(\Rightarrow z=\sqrt{\left(x-z\right)\left(y-z\right)}\left(z>0\right)\)

Lại có: \(x+y=x-z+y-z+2z\)

\(=\left(x-z\right)+\left(y-z\right)+2\sqrt{\left(x-z\right)\left(y-z\right)}=\left(\sqrt{x-z}+\sqrt{y-z}\right)^2\)

Suy ra \(\sqrt{x+y}=\sqrt{x-z}+\sqrt{y-z}\) (ĐPCM)

`Answer:`

\(\frac{xy}{ay+bx}=\frac{yz}{bz+cy}=\frac{zx}{cx+ax}=\frac{x^2+y^2+z^2}{a^2+b^2+c^2}\left(1\right)\)

Theo đề ra, có: \(\frac{xy}{ay+bx}=\frac{yz}{bz+cy}=\frac{zx}{cx+az}\)

\(\Rightarrow\frac{xyz}{ayz+bxz}=\frac{xyz}{bxz+cxy}=\frac{xyz}{cxy+ayz}\)

\(\Rightarrow ayz+bxz=bxz+cxy=cxy+ayz\)

\(\Rightarrow\hept{\begin{cases}ayz+bxz=bxz+cxy\\ayz+bxz=cxy+ayz\\bxz+cxy=cxy+ayz\end{cases}}\)

\(\Rightarrow\hept{\begin{cases}ayz=cxy\\bxz=cxy\\bxz=ayz\end{cases}}\)

\(\Rightarrow\hept{\begin{cases}az=cx\\bz=cy\\bx=ay\end{cases}}\left(2\right)\)

Thế (2) và (1): \(\frac{xy}{2ay}=\frac{yz}{2bz}=\frac{xz}{2cx}=\frac{x^2+y^2+z^2}{a^2+b^2+c^2}\)

\(\Rightarrow\frac{x}{2a}=\frac{y}{2b}=\frac{z}{2c}=\frac{x^2+y^2+z^2}{a^2+b^2+c^2}\left(3\right)\)

\(\Rightarrow\frac{x^2}{4a^2}=\frac{y^2}{4b^2}=\frac{z^2}{4c^2}=\frac{\left(x^2+y^2+z^2\right)^2}{\left(a^2+b^2+c^2\right)^2}=\frac{x^2+y^2+z^2}{4a^2+4b^2+4c^2}\)

\(\Rightarrow\frac{x^2+y^2+z^2}{a^2+b^2+c^2}=\frac{1}{4}\)

Thế (3) vào (2): \(\frac{x}{2a}=\frac{y}{2b}=\frac{z}{2c}=\frac{1}{4}\)

\(\Rightarrow\hept{\begin{cases}x=\frac{a}{2}\\y=\frac{b}{2}\\z=\frac{c}{2}\end{cases}}\)

Lời giải:

$2\text{VT}=2(x+y+z)-4(xy+yz+xz)+8xyz$

$=(2x-1)(2y-1)(2z-1)+1$

Do $x,y,z\in [0;1]$ nên $-1\leq 2x-1, 2y-1, 2z-1\leq 1$

$\Rightarrow (2x-1)(2y-1)(2z-1)\leq 1$

$\Rightarrow 2\text{VT}\leq 2$

$\Rightarrow \text{VT}\leq 1$
Ta có đpcm.

Dấu "=" xảy ra khi $(x,y,z)=(1,1,1), (0,0,1)$ và hoán vị.

Đáp án là A

\(\dfrac{x+y}{z}+\dfrac{y+z}{x}+\dfrac{x+z}{y}=\dfrac{x^2y+xy^2+y^2z+yz^2+x^2z+xz^2}{xyz}=\dfrac{-3xyz}{xyz}=-3\)

đề cho xy+yz+xz=0 nhân cả 2 vế với -z

=>-xyz-\(z^2\left(y+x\right)\)=0

=>-xyz=\(z^2x+z^2y\)

cmtt bạn nhân với -y và -z

=>-3xyz=\(x^2y+xy^2+y^2z+yz^2+x^2z+xz^2\)

Do \(x\in\left[-1;2\right]\Rightarrow\)\(\left(x+1\right)\left(x-2\right)\le0\Leftrightarrow x^2\le x+2\)

Tương tự: \(y^2\le y+2\) ; \(z^2\le z+2\)

Cộng vế: \(x^2+y^2+z^2\le x+y+z+6=6\) (đpcm)

Mặt khác \(x;y;z\in\left[-1;2\right]\Rightarrow\left(x+1\right)\left(y+1\right)\left(z+1\right)\ge0\)

\(\Leftrightarrow xyz+xy+yz+zx+x+y+z+1\ge0\)

\(\Leftrightarrow xyz+xy+yz+zx+1\ge0\)

\(\Leftrightarrow2xyz+2\ge-2\left(xy+yz+zx\right)\)

\(\Leftrightarrow2xyz+2\ge\left(x^2+y^2+z^2\right)-\left(x+y+z\right)^2\)

\(\Leftrightarrow2xyz+2\ge x^2+y^2+z^2\) (đpcm)