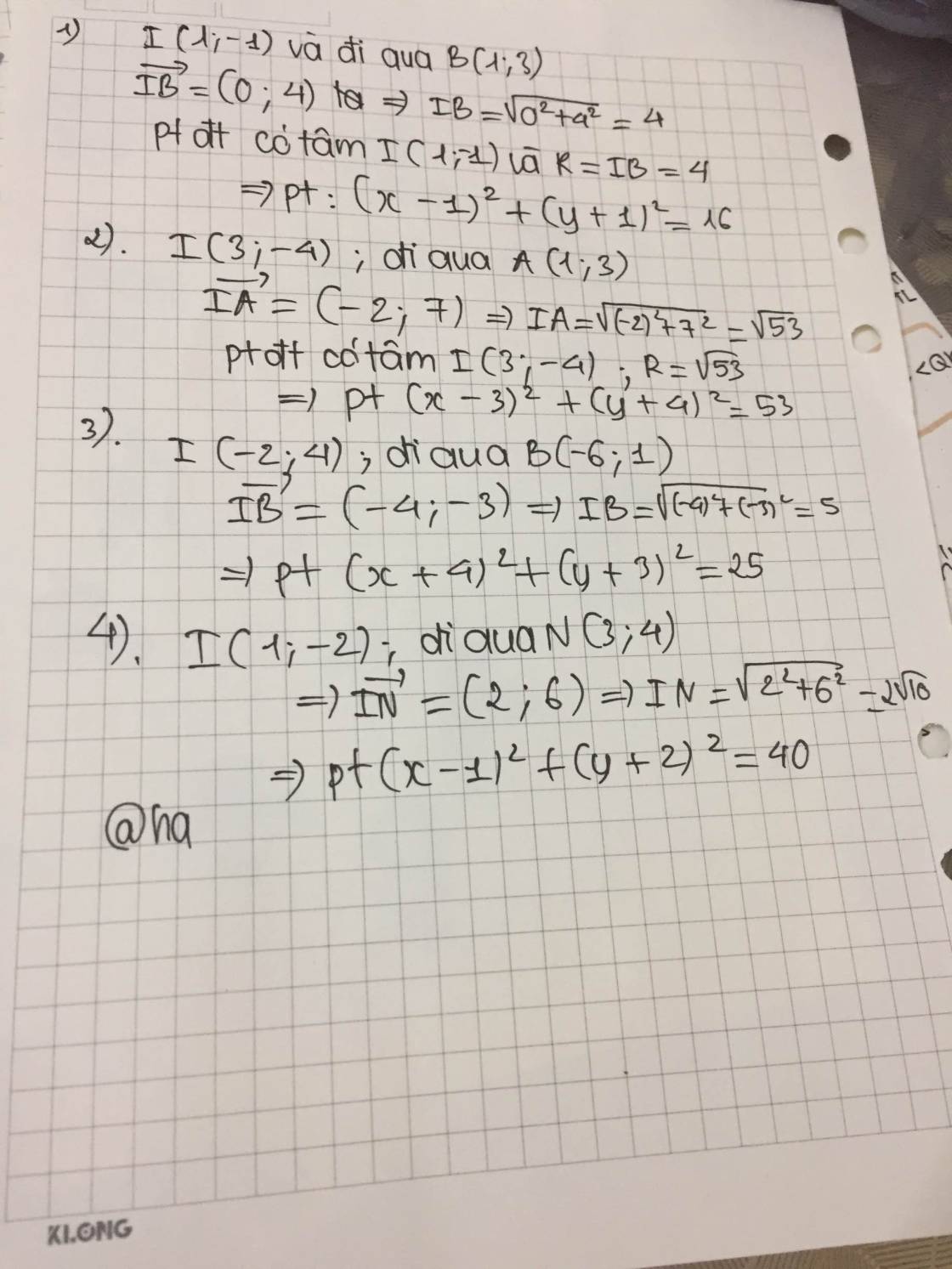1. Viết pt đg tròn(C) đi qua A(1;0) , B(0;1) và (C) có tâm I thuộc đg thẳng denta : x +y -2=0

Những câu hỏi liên quan
1) Viết pt đường tròn tâm l (1,-1) và đi qua điểm B (1,3) 2) Viết pt đường tròn tâm l (3,-4) và đi qua điểm A (1,3) 3) Viết pt đường tròn tâm l ( -2,4) , đi qua điểm B (-6,1) 4) viết pt đường tròn tâm l (1,-2) và đi qua điểm N ( 3,4) Giúp vs bạn
9. Cho đg thẳng (d) x -2y +1=0. Nếu đg thẳng (denta) đi qua M(1;-1) và song song vs (d) thì (denta) có pt?
10. Cho 3 điểm A(1;-2), B(5;-4) , C(-1;4). Đg cao AA' của tg ABC có pt?
18. Viết pt đg thẳng đi qua điểm M(2;-3) và cắt hai trục toạ độ tại hai điểm A và B sao cho tg OAB vuông cân.
9/ \(\Delta//\left(d\right)\Rightarrow\overrightarrow{n_d}=\left(1;-2\right)\)
\(\Rightarrow\left(d\right):\left(x-1\right)-2\left(y+1\right)=0\)
\(\left(d\right):x-2y-3=0\)
10/ \(\overrightarrow{BC}=\left(-6;8\right)\)
PT đường cao AA' nhận vecto BC làm vtpt
\(\Rightarrow\overrightarrow{n_{AA'}}=\overrightarrow{u_{BC}}=\left(-6;8\right)\)
\(AA':-6\left(x-1\right)+8\left(y+2\right)=0\)
\(AA'=-6x+8y+22=0\)
18/ Trong quá trình làm bài, mình rút ra kết luận sau: Nếu một đường thẳng chắn 2 trục toạ độ 2 đoạn có độ dài bằng nhau thì ptđt có hệ số góc là \(k=\pm1\)
Để mình chứng minh lại:
Đường thẳng có dạng : y= ax+b
\(\Rightarrow\) Nó cắt trục Oy tại điểm có toạ độ là \(\left(0;b\right)\)
Và cắt trục Ox tại điểm có toạ độ là \(\left(-\frac{b}{a};0\right)\)
Vì khoảng cách từ O đến từng điểm là như nhau
\(\Rightarrow\left|b\right|=\left|\frac{b}{a}\right|\Leftrightarrow\left[{}\begin{matrix}b=\frac{b}{a}\\b=-\frac{b}{a}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=1\\a=-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\overrightarrow{u}=\left(1;1\right)\\\overrightarrow{u}=\left(1;-1\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left(d\right):x-2+y+3=0\\\left(d\right):x-2-y-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}\left(d\right):x+y+1=0\\\left(d\right):x-y-5=0\end{matrix}\right.\)
Đúng 0
Bình luận (0)
\(A(1;-2),B(3;4),C(-1;0)\)
a) Viết pt đường tròn đi qua A,B và có R=5
b) Viết pt đường tròn đi qua A,B và tiếp xúc với đường thẳng AC
a, Phương trình đường thẳng AB: \(\dfrac{x-3}{2}=\dfrac{y-4}{6}\Leftrightarrow3x-y-5=0\)
Trung điểm I của AB có tọa độ: \(\left\{{}\begin{matrix}x_I=\dfrac{1+3}{2}=2\\y_I=\dfrac{4-2}{2}=1\end{matrix}\right.\Rightarrow I=\left(2;1\right)\)
Phương trình trung trực của AB: \(x+3y-5=0\)
Giả sử \(O=\left(5-3m;m\right)\) là tâm đường tròn
Ta có: \(OA=5\Leftrightarrow\left(3m-4\right)^2+\left(m+2\right)^2=25\)
\(\Leftrightarrow\left(3m-4\right)^2+\left(m+2\right)^2=25\)
\(\Leftrightarrow2m^2-4m-1=0\)
\(\Leftrightarrow m=\dfrac{2\pm\sqrt{6}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}O=\left(\dfrac{4-3\sqrt{6}}{2};\dfrac{2+\sqrt{6}}{2}\right)\\O=\left(\dfrac{4+3\sqrt{6}}{2};\dfrac{2-\sqrt{6}}{2}\right)\end{matrix}\right.\)
TH1: \(O=\left(\dfrac{4-3\sqrt{6}}{2};\dfrac{2+\sqrt{6}}{2}\right)\)
Phương trình đường tròn:
\(\left(x-\dfrac{4-3\sqrt{6}}{2}\right)^2+\left(y-\dfrac{2+\sqrt{6}}{2}\right)^2=25\)
TH2: \(O=\left(\dfrac{4+3\sqrt{6}}{2};\dfrac{2-\sqrt{6}}{2}\right)\)
Phương trình đường tròn:
\(\left(x-\dfrac{4+3\sqrt{6}}{2}\right)^2+\left(y-\dfrac{2-\sqrt{6}}{2}\right)^2=25\)
Kết luận: Phương trình đường tròn:
\(\left(x-\dfrac{4-3\sqrt{6}}{2}\right)^2+\left(y-\dfrac{2+\sqrt{6}}{2}\right)^2=25\) hoặc \(\left(x-\dfrac{4+3\sqrt{6}}{2}\right)^2+\left(y-\dfrac{2-\sqrt{6}}{2}\right)^2=25\)
Đúng 1
Bình luận (0)
b, Phương trình đường thẳng AC: \(x+y+1=0\)
Phương trình đường thẳng OA: \(x-y-3=0\)
Giả sử \(O=\left(m;m-3\right)\) là tâm đường tròn
Ta có: \(OA=OB\Leftrightarrow\left(1-m\right)^2+\left(1-m\right)^2=\left(3-m\right)^2+\left(7-m\right)^2\)
\(\Leftrightarrow m=\dfrac{7}{2}\)
\(\Rightarrow O=\left(\dfrac{7}{2};\dfrac{1}{2}\right)\)
Bán kính: \(R=OA=\sqrt{\left(1-\dfrac{7}{2}\right)^2+\left(-2-\dfrac{1}{2}\right)^2}=\dfrac{5\sqrt{2}}{2}\)
Phương trình đường tròn:
\(\left(x-\dfrac{7}{2}\right)^2+\left(y-\dfrac{1}{2}\right)^2=\dfrac{25}{2}\)
Đúng 0
Bình luận (0)
trong mp Oxy, cho 2 điểm A(-2;3), B(1;-1)
a) viết pt tổng quát đg trung trực AB
b) viết pt đg tròn đi qua B và có tâm là A
c) viết pt đg tròn tâm đã cho biết tiếp tuyến song song với đg thg \(\Delta:3x+4y-1=0\)
\(\overrightarrow{AB}=\left(3;-4\right)\) , gọi M là trung điểm AB \(\Rightarrow M\left(-\frac{1}{2};1\right)\)
Trung trực AB qua M và vuông góc AB nên có pt:
\(3\left(x+\frac{1}{2}\right)-4\left(y-1\right)=0\Leftrightarrow6x-8y+11=0\)
b/ \(AB=\sqrt{3^2+\left(-4\right)^2}=5\Rightarrow R=AB=5\)
Pt đường tròn: \(\left(x+2\right)^2+\left(y-3\right)^2=25\)
c/ Chắc là viết pttt?
Tiếp tuyến song song denta nên có pt: \(3x+4y+c=0\) (\(c\ne-1\))
d tiếp xúc (C) nên \(d\left(A;d\right)=R\Leftrightarrow\frac{\left|3.\left(-2\right)+4.3+c\right|}{\sqrt{3^2+4^2}}=5\)
\(\Leftrightarrow\left|c+6\right|=25\Rightarrow\left[{}\begin{matrix}c=19\\c=-31\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}3x+4y+19=0\\3x+4y-21=0\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho A(1;-3); B(-2; 3)
a) Viết pt đường thẳng AB
b) Viết pt đg thẳng (d) đi qua C(1; 3) và vuông góc với AB
a) ta có : phương trình đường thẳng \(AB\) có dạng \(\left(d_{AB}\right):y=ax+b\)
vì \(A\in\left(d_{AB}\right)\Rightarrow-3=a+b\) và vì \(B\in\left(d_{AB}\right)\Rightarrow3=-2a+b\)
từ đó ta có hệ \(\left\{{}\begin{matrix}a+b=-3\\-2a+b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=-1\end{matrix}\right.\)
vậy phương trình đường thẳng \(AB\) là \(y=-2x-1\)
b) ta có : \(\left(d\right):y=ax+b\)
vì \(\left(d\right)\perp AB\Rightarrow\) \(=-2a=-1\Leftrightarrow a=\dfrac{1}{2}\)
ta có : \(C\in\left(d\right)\Rightarrow3=a+b\)
từ đó ta có hệ \(\left\{{}\begin{matrix}a=\dfrac{1}{2}\\a+b=3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=\dfrac{5}{2}\end{matrix}\right.\)
vậy \(\left(d\right):y=\dfrac{1}{2}x+\dfrac{5}{2}\)
Đúng 1
Bình luận (1)
Cho A(1;-3); B(-2; 3)
a) Viết pt đường thẳng AB
b) Viết pt đg thẳng (d) đi qua C(1; 3) và vuông góc với AB
a: Gọi (d): y=ax+b là phương trình (AB)
Theo đề, ta có:
a+b=-3 và -2a+b=3
=>a=-2; b=-1
=>y=-2x-1
b: (d) vuông góc với AB nên (d): y=1/2x+b
Thay x=1 và y=3 vào (d), ta được:
b+1/2=3
=>b=5/2
Đúng 0
Bình luận (0)
30. Viết pt tham số của đg thẳng đi qua 2 điểm A( 3;-7) và B(1;-7)
31. Trong mặt phẳng toạ độ Oxy , viết pt tổng quát của đg trung trực của đoạn thẳng AB với A (2;3) và B(-4;-1)
32. Trong mặt phẳng toạ độ Oxy , viết pt tổng quát của đg thẳng đi qua giao điểm của d1 : 3x - 5y +30 và d2 5x -2y +4 0 đồng thời song song với d3 2x - y +40
33. Trong mặt phẳng toạ độ Oxy , cho tâm tâm s ABC vs A( -1;2) , B(1;1) , C(2;-1). Viết pt tổng quát đg cao AH của tam giác ABC.
34. Cho tg ABC có toạ độ các đỉ...
Đọc tiếp
30. Viết pt tham số của đg thẳng đi qua 2 điểm A( 3;-7) và B(1;-7)
31. Trong mặt phẳng toạ độ Oxy , viết pt tổng quát của đg trung trực của đoạn thẳng AB với A (2;3) và B(-4;-1)
32. Trong mặt phẳng toạ độ Oxy , viết pt tổng quát của đg thẳng đi qua giao điểm của d1 : 3x - 5y +3=0 và d2 5x -2y +4 =0 đồng thời song song với d3 2x - y +4=0
33. Trong mặt phẳng toạ độ Oxy , cho tâm tâm s ABC vs A( -1;2) , B(1;1) , C(2;-1). Viết pt tổng quát đg cao AH của tam giác ABC.
34. Cho tg ABC có toạ độ các đỉnh là A(-1;1) , B(4;7) và C(3;-2) , M là trung điểm của đoạn thẳng AB. Viết pt tham số của đg thẳng CM là?
14. Trong mặt phẳng toạ độ Oxy cho hai điểm A(3;-4), B(0;6). Viết pt tổng quát của đg thẳng AB.
16. Trong mặt phẳng toạ độ Oxy , viết pt tổng quát của đg thẳng d đi qua A(2;1) và song song và đg thẳng denta: 3x -2y +3=0.
17. Trong mặt phẳng toạ độ Oxy , viết pt tổng quát của đg thẳng d đi qua điểm I(4;-1) và vuông góc với đg thẳng denta : x+y-2017=0.
14.
\(\overrightarrow{AB}=\left(-3;10\right)\Rightarrow\) đường thẳng AB nhận \(\left(10;3\right)\) là 1 vtpt
Phương trình AB:
\(10\left(x-3\right)+3\left(y+4\right)=0\Leftrightarrow10x+3y-18=0\)
16.
Do d song song denta nên d nhận \(\left(3;-2\right)\) là 1 vtpt
Phương trình d:
\(3\left(x-2\right)-2\left(y-1\right)=0\Leftrightarrow3x-2y-4=0\)
17. Cho d vuông góc denta nên d nhận \(\left(1;-1\right)\) là 1vtpt
Phương trình d:
\(1\left(x-4\right)-1\left(y+1\right)=0\Leftrightarrow x-y-5=0\)
Đúng 0
Bình luận (0)
Cho đg tròn (C) có tâm I thuộc trục Ox và đi qua 2 điểm M(1;-2), N(3;-1). Viết pt đg tròn (C)
Gọi A là trung điểm \(MN\Rightarrow A\left(2;-\frac{3}{2}\right)\)
\(\overrightarrow{MN}=\left(2;1\right)\)
Trung trực d của MN đi qua A và vuông góc MN có pt:
\(2\left(x-2\right)+1\left(y+\frac{3}{2}\right)=0\Leftrightarrow2x+y-\frac{5}{2}=0\)
I là giao của d và Ox nên tọa độ thỏa mãn: \(\left\{{}\begin{matrix}y=0\\2x+y-\frac{5}{2}=0\end{matrix}\right.\)
\(\Rightarrow I\left(\frac{5}{4};0\right)\) \(\Rightarrow\overrightarrow{AI}=\left(\frac{1}{4};2\right)\Rightarrow R=\sqrt{\left(\frac{1}{4}\right)^2+2^2}=\frac{\sqrt{65}}{4}\)
Phương trình: \(\left(x-\frac{5}{4}\right)^2+y^2=\frac{65}{16}\)
Đúng 0
Bình luận (0)