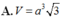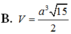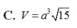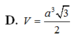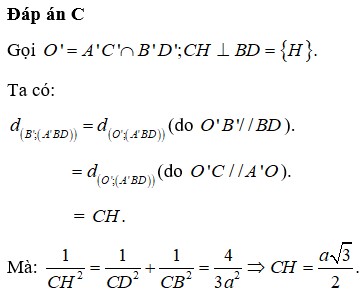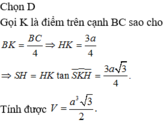trong mặt phẳng Oxy cho hình chữ nhật ABCD có H là hình chiếu vuông góc của A trên BD. biết M (6;3), N (5;0) theo thứ tự là trung điểm của BH, CD .Điểm A thuộc đường thẳng d: 4x-y + 5 = 0. Xác định tọa độ các đỉnh A,B,C,D

Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có hình chiếu vuông góc của A lên đường thẳng BD là H(-1/5;2/5), điểm M(0;-1) là trung điểm cạnh BC và điểm N(7/5;-4/5) là trung điểm của đoạn HD. Tìm tọa độ các đỉnh của hình chữ nhật ABCD.
Trong mặt phẳng Oxy cho HCN ABCD có điểm B (1;3) và diện tích là 30goij E là điểm nằm trên cạnh BC sao cho EC =2EB điểm H(5/2;5/2) là hình chiếu vuông góc trên DE Biết C có tung độ âm , Tìm tọa độ các hình chữ nhật
Cho lăng trụ ABCD.ABCD có đáy ABCD là hình chữ nhật,
A
B
a
,
A
D
a
3
. Hình chiếu vuông góc của điểm A trên mặt phẳng (ABCD) trùng với giao điểm AC và BD. Tính khoảng cách từ điểm B đến mặt phẳng (ABD) A.
a...
Đọc tiếp
Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật, A B = a , A D = a 3 . Hình chiếu vuông góc của điểm A' trên mặt phẳng (ABCD) trùng với giao điểm AC và BD. Tính khoảng cách từ điểm B' đến mặt phẳng (A'BD)
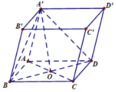
A. a 3 3
B. a 3 6
C. a 3 2
D. a 3 4
Cho lăng trụ ABCD. ABCD có đáy ABCD là hình chữ nhật, ABa,
A
D
a
3
. Hình chiếu vuông góc của điểm A trên mặt phẳng (ABCD) trùng với giao điểm AC và BD. Tính khoảng cách từ điểm B đến mặt phẳng (ABD) A.
a
3
3
B.
a
3
6
C.
a...
Đọc tiếp
Cho lăng trụ ABCD. A'B'C'D' có đáy ABCD là hình chữ nhật, AB=a, A D = a 3 . Hình chiếu vuông góc của điểm A' trên mặt phẳng (ABCD) trùng với giao điểm AC và BD. Tính khoảng cách từ điểm B' đến mặt phẳng (A'BD)
A. a 3 3
B. a 3 6
C. a 3 2
D. a 3 4
Cho lăng trụ ABCD. ABCD có đáy ABCD là hình chữ nhật, AB3, AD
a
3
. Hình chiếu vuông góc của điểm A trên mặt phẳng (ABCD) trùng với giao điểm AC và BD. Tính khoảng cách từ điểm B đến mặt phẳng (ABD) A.
a
3
3
B.
a
...
Đọc tiếp
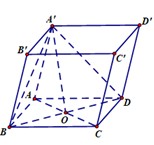
Cho lăng trụ ABCD. A'B'C'D' có đáy ABCD là hình chữ nhật, AB=3, AD= a 3 . Hình chiếu vuông góc của điểm A' trên mặt phẳng (ABCD) trùng với giao điểm AC và BD. Tính khoảng cách từ điểm B' đến mặt phẳng (A'BD)
A. a 3 3
B. a 3 6
C. a 3 2
D. a 3 4
Cho lăng trụ
A
B
C
D
.
A
B
C
D
có đáy ABCD là hình chữ nhật
A
B
a
,
A
D
a
3
.
Hình chiếu vuông góc của điểm A¢ trên mặt phẳng (ABCD) trùng với giao điểm AC và BD. Tính khoảng cách từ điểm B¢ đến mặt phẳng (A’BD) là A.
a
3
3
B. ...
Đọc tiếp
Cho lăng trụ A B C D . A ' B ' C ' D ' có đáy ABCD là hình chữ nhật A B = a , A D = a 3 . Hình
chiếu vuông góc của điểm A¢ trên mặt phẳng (ABCD) trùng với giao điểm AC và BD. Tính khoảng cách từ điểm B¢ đến mặt phẳng (A’BD) là
A. a 3 3
B. a 3 4
C. a 3 2
D. a 3 6
Đáp án C.
Kẻ A H ⊥ B D H ∈ B D mà
A ' O ⊥ A B C D ⇒ A ' O ⊥ A H ⇒ A H ⊥ A ' B D .
Ta có d B ' , A ' B D = d A , A ' B D = A H = A B . A D A B 2 + A D 2 = a 3 2
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Gọi O là giao điểm của AC và BD. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) là trung điểm H của đoạn OA và góc
S
D
;
A
B
C
D
^
60
°
. Gọi a là góc giữa...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Gọi O là giao điểm của AC và BD. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) là trung điểm H của đoạn OA và góc S D ; A B C D ^ = 60 ° . Gọi a là góc giữa hai mặt phẳng (SCD) và (ABCD). Tính tanα
A. tan α = 4 15 9
B. tan α = 30 12
C. tan α = 10 3
D. tan α = 30 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Gọi O là giao điểm của AC và BD. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) là trung điểm H của đoạn OA và góc
S
D
,
(
A
B
C
D
)
^
60
°
. Gọi a là góc giữa hai mặt phẳng (SCD) và (ABCD). Tính...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Gọi O là giao điểm của AC và BD. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) là trung điểm H của đoạn OA và góc S D , ( A B C D ) ^ = 60 ° . Gọi a là góc giữa hai mặt phẳng (SCD) và (ABCD). Tính tana
A. tana = 4 15 9
B. tana = 30 12
C. tana = 10 3
D. tana = 30 3
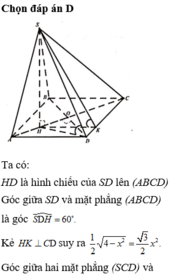
Chọn đáp án D
Ta có: HD là hình chiếu của SD lên mặt phẳng (ABCD).
Góc giữa SD và mặt phẳng (ABCD) là góc S D H ^ = 60 °
Kẻ HK
⊥
CD suy ra 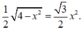
Góc giữa hai mặt phẳng (SCD) và (ABCD) là góc S K H ^ = α
Ta có: 
![]()

Mặt khác: HK//AD ![]()
![]()
Vậy: 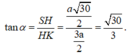
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB a, BC 2a, hình chiếu vuông góc của đỉnh S trên mặt đáy là trung điểm H của OA. Biết rằng mặt phẳng (SBC) tạo với mặt phẳng đáy một góc
60
°
. Tính thể tích V của khối chóp S.ABCD. A.
V
a
3
3
B.
V
a
3
15...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB = a, BC = 2a, hình chiếu vuông góc của đỉnh S trên mặt đáy là trung điểm H của OA. Biết rằng mặt phẳng (SBC) tạo với mặt phẳng đáy một góc 60 ° . Tính thể tích V của khối chóp S.ABCD.
A. V = a 3 3
B. V = a 3 15 2
C. V = a 3 15
D. V = a 3 15 2
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O,
A
B
a
,
B
C
2
a
, hình chiếu vuông góc của đỉnh S trên mặt đáy là trung điểm H của OA. Biết rằng mặt phẳng (SBC) tạo với mặt phẳng đáy một góc
60
0
. Tính thể tích V của khối chóp S.ABCD.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, A B = a , B C = 2 a , hình chiếu vuông góc của đỉnh S trên mặt đáy là trung điểm H của OA. Biết rằng mặt phẳng (SBC) tạo với mặt phẳng đáy một góc 60 0 . Tính thể tích V của khối chóp S.ABCD.