cho 2018 số tự nhiên là a1;a2;a3;.....a2018 đều là các số lớn hơn 1 thỏa mãn điều kiện 1/a21+1/a22+1/a23+.....+1/a22018=1.Chứng minh rằng trong 2018 số này ,ít nhất sẽ có 2 số bằng nhau.

Những câu hỏi liên quan
cho P thuộc N tách P thành tổng của 2018 số tự nhiên a1,a2,a3,....,a2018 biết tổng lập phương cuả 2018 số đó chia 6 dư 5 hỏi số P chia cho 6 dư mấy
các bạn nhớ làm nhanh lên nhé , bạn nào làm đúng và nhanh tớ sẽ like cho
Tớ nêu ý kiến =) bài chưa qua kiểm định nhé ^^
Lấy tổng lập phương 2018 số đó trừ đi P sẽ đc 1 hiệu chia hết cho 6
VD nhé : a1^3 - a1 = a1.(a1^2-1) = a1.(a1-1).(a1+1) là tích 3 số tự nhiên liên tiếp nên chia hết cho 6
Mấy cái còn lại cx tương tự như thế thì hiệu nhận đc đúng là chia hết cho 6 đúng ko?
Thế thì P chia 6 dư 5 rồi =D
Đúng 0
Bình luận (0)
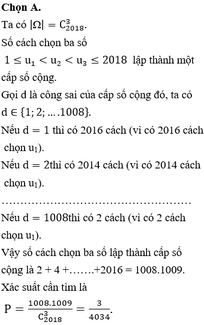
Cho 2018 số tự nhiên liên tiếp 1, 2, 3, …,2018. Chọn ngẫu nhiên ba số tự nhiên từ các số đã cho. Tính xác suất để chọn được ba số có một số là trung bình cộng của hai số còn lại A.
3
4034
B.
5
4034
C.
7
4034
D.
...
Đọc tiếp
Cho 2018 số tự nhiên liên tiếp 1, 2, 3, …,2018. Chọn ngẫu nhiên ba số tự nhiên từ các số đã cho. Tính xác suất để chọn được ba số có một số là trung bình cộng của hai số còn lại
A. 3 4034
B. 5 4034
C. 7 4034
D. 9 4034
Cho 2018 số tự nhiên liên tiếp 1, 2, 3, …,2018. Chọn ngẫu nhiên ba số tự nhiên từ các số đã cho. Tính xác suất để chọn được ba số có một số là trung bình cộng của hai số còn lại A.
3
4034
B.
5
4034
C.
7
4034
D.
9
4034
Đọc tiếp
Cho 2018 số tự nhiên liên tiếp 1, 2, 3, …,2018. Chọn ngẫu nhiên ba số tự nhiên từ các số đã cho. Tính xác suất để chọn được ba số có một số là trung bình cộng của hai số còn lại
A. 3 4034
B. 5 4034
C. 7 4034
D. 9 4034
cho n số nguyên bất kỳ a1,a2,a3,...,an (n thuộc N n_>2) chứng tỏ nếu n là số tự nhiên chia 4 dư 1 thì tổng A =|a1-a2+1| + |a2-a3+2| + |a3-a4+3|+...+|an-1 - an +n-1| + |an-a1+n| là số tự nhiên lẻ
Cho 2020 số tự nhiên (>0) a1, a2, a3,...,a2020 sao cho 1/a1 + 1/a2 + ... + 1/a2020 = 1. CMR tồn tại ít nhất 1 số ak là số chẵn.
Xem chi tiết
Tìm số tự nhiên n lớn nhất sao cho 2015 viết được dưới dạng:
2015 = a1 + a2 +....+an với các số a1,a2,...,an đều là hợp số
khi chia số tự nhiên K cho số tự nhiên D ta được thương là 10000 và dư là Q.Tìm thương khi chia số 2018(K-Q)+2019D cho D
tìm 4 số tự nhiên a1<a2<a3<a4 sao cho tất cả các số d1=a1-a3,d2=a3-a2,d3=a2-a1,d4=a4-a2,d5=a3-a1,d6=a4-a1 đều là số nguyên tố trong đó có thể có các số nguyên tố bằng nhau
chon dai di thoi
a1=1
a2=3
=>d3=2
d1=a1-a3 de sai roi a1<a3 khong co d1
Đúng 0
Bình luận (0)
cho x, y là các số tự nhiên lớn hơn 1 thỏa mãn x^2017=y^2018. Hãy tìm số tự nhiên x, biết y là số tự nhiên nhỏ nhất.
Ai đúng, tick luôn
do y la so tu nhien nho nhat nen y=0
=>y^2018=0
=>x^2017=0
=>x=0
Đúng 0
Bình luận (0)
Cho a1,a2,a3...,a2018 là 2018 số thực thỏa mãn ak=(2k+1)/(k^2+k)^2, với k=1, 2, 3, ...2018. Tính S2018=a1+a2+...+a2018 giúp mik với ạ